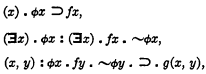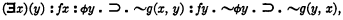Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. iv
-
- Article
-
- You have access
- Export citation
Research Article
Symbols, signs, and signals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 41-52
-
- Article
- Export citation
An informal exposition of proofs of Gödel's theorems and Church's theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 53-60
-
- Article
- Export citation
A formal proof of Gödel's theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 61-68
-
- Article
- Export citation
On the independence of the axioms of definiteness (Axiome der Bestimmtheit)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 69-72
-
- Article
- Export citation
A system of strict implication
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-76
-
- Article
- Export citation
A theorem on deducibility for second-order functions1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 77-79
-
- Article
- Export citation
Definition by induction in quine's new foundations for mathematical logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 80-81
-
- Article
- Export citation
Reviews
Rudolf Carnap. The logical syntax of language. Harcourt, Brace and Co., New York1937; Kegan Paul, Trench, Trubner and Co., London 1937; xvi + 352 pp. (English edition of 35212, with material from 35214 and 35215. Translation by Amethe Smeaton.)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 82-87
-
- Article
- Export citation
Hans Hermes. Semiotik. Eine Theorie der Zeichengestalten als Grundlage für Untersuchungen von formalisierten Sprachen. Forschungen zur Logik und zur Grundlegung der exakten Wissenschaften, new series, no. 5. S. Hirzel, Leipzig1938, 22 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 87-88
-
- Article
- Export citation
M. H. Stone. Applications of the theory of Boolean rings to general topology. Transactions of the American Mathematical Society, vol. 41 (1937). pp. 375–481.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 88-89
-
- Article
- Export citation
Katudi Ono. Logische Untersuchungen über die Grundlagen der Mathematik. Journal of the Faculty of Science, Imperial University of Tokyo, section I, vol. 3 part 7 (1938), pp. 329–389.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 89-90
-
- Article
- Export citation
E. V. Huntington. Note on a recent set of postulates for the calculus of propositions. The journal of symbolic logic, vol. 4 (1939), pp. 10–14.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 90
-
- Article
- Export citation
Francesco Orestano. A propos de mes “Nouvelles vues logiques.” Revue de métaphysique et de morale, vol. 46 (1939), pp. 41–55.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 90-91
-
- Article
- Export citation
M. Barzin. Cours de logique. Polycopié. Desoer, Liége1937, deux tomes, 63 + 117 pages.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 91
-
- Article
- Export citation
E. Hüffer. Logistiek (La logistique). Vraagstukken uit de logica. Verslag van de vijfde algemeene vergadering der Vereeniging voor Thomistische Wijsbegeerte (supplément de Studia Calholica), Dekker & van de Vegt, Nijmegen1938, p. 63–85. Discussion, p. 85–89.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 91
-
- Article
- Export citation
Eugen Gh. Mihailescu. Recherches sur les formes normales par rapport à l'équivalence et la disjonction, dans le calcul des propositions. Annales scientifiques de l'Université de Jassy, première partie, t. 25 (1939), p. 73–152.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 91-92
-
- Article
- Export citation
Kazimierz Makarczyk. Technika rachunku logicznego (La technique du calcul logique). Varsovie1938, 35 pages.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 92
-
- Article
- Export citation
Józef Pepis. O zagadnieniu rozstrzygalności w zakresie wȩzszego rachunku funkcyjnego (Über das Entscheidungsproblem des engeren logischen Funktionenkalküls). Polnisch mit deutscher Zusammenfassung. Archiwum Towarzystwa Naukowego we Lwowie, Dział III, Bd. 7 H. 8 (1937), S. 1–172.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 93
-
- Article
- Export citation
S. C. Kleene. On notation for ordinal numbers. The journal of symbolic logic, Bd. 3 (1938), S. 150–155.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 93-94
-
- Article
- Export citation

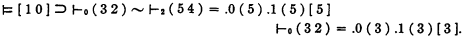
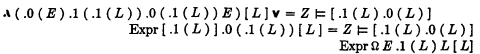
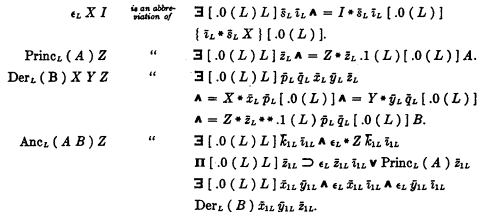
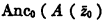
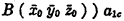 will be called an
will be called an 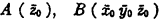 will be called respectively the
will be called respectively the 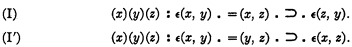
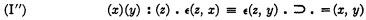
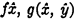 of a set of postulates defining such a series either is implied by the postulates or is inconsistent with them. It is here understood, in accordance with the usual convention, that when we speak of a function on the base
of a set of postulates defining such a series either is implied by the postulates or is inconsistent with them. It is here understood, in accordance with the usual convention, that when we speak of a function on the base