Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T20:19:29.873Z Has data issue: false hasContentIssue false
  • English
  • Français

On the independence of the axioms of definiteness (Axiome der Bestimmtheit)

Published online by Cambridge University Press:  12 March 2014

Abraham Robinsohn
Abraham Robinsohn*
Affiliation:
Einstein Institute of Mathematics, Hebrew University, Jerusalem
Get access Rights & Permissions [Opens in a new window]

Extract

The question of the independence of the axioms of the theory of sets has been dealt with in a number of works, although not in a final manner. The writer will be concerned solely with the axiomatic system of Zermelo and Fraenkel, and only with that feature of the system whereby all the objects of the underlying domain are sets (so that there is no difference between objects in general and sets in particular).

A special place among the axioms is occupied by a purely relational one, an axiom of definiteness, which establishes the character of equality within the system.

Zermelo introduces equality intensionally—if two symbols x and y represent the same object, we write = (x, y). According to this there is no necessity for axioms to assure the interchangeability of equal objects as arguments of the primitive relation ϵ( , ). For under the intensional interpretation it is clear that:

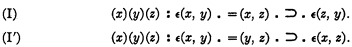
Similarly it is clear that there is no necessity for a separate axiom that will assure to equality the properties of an equivalence relation. Therefore Zermelo introduces only the following axiom of extensionality:

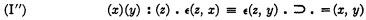
(if one set is a subset of another set, and the second set is also a subset of the first, then the two sets are equal).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 4 , Issue 2 , June 1939 , pp. 69 - 72
Copyright
Copyright © Association for Symbolic Logic 1939

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Fraenkel, A., Mathematische Annalen, vol. 86 (1922), pp. 234–237CrossRefGoogle Scholar, and Sitzungsberichte der Preussischen Akademie der Wissenschaften, Phys.-math. Klasse, 1922, pp. 253–257Google Scholar; Lennes, N. J., Bulletin of the American Mathematical Society, vol. 28 (1922), p. 300Google Scholar; Vieler, H., Untersuchungen über Unabhängigkeit und Tragweite der Axiome der Mengenlehre etc., dissertation Marburg 1926Google Scholar.

2 Zermelo, E., Mathematische Annalen, vol. 65 (1908), pp. 107–128CrossRefGoogle Scholar; Fraenkel, A., Journal für die reine und angewandte Mathematik, vol. 155 (1926), pp. 129–158Google Scholar, and Einleitung in die Mengenlehre, 3rd edn., Berlin 1928, §16Google Scholar.

3 Fraenkel, A., Journal für die reine und angewandte Mathematik, vol. 157 (1927), pp. 79–81Google Scholar; H. Vieler, loc. cit., pp. 9–11; Ackermann, W., Mathematische Annalen, vol. 115 (1937), p. 8Google Scholar.

4 I' may be proved by means of the axioms I, IV, V in the following way. I implies immediately =(x, y)·⊃·(t)·ϵ(x, t)≡ϵ(y, t). By IV there exists some τ that contains x and therefore contains y. Let us suppose, contrary to our assertion, that there exists some ρ such that ϵ(ρ, x) and ˜(ρ, y). Then (by V)τρϵx, the set of those elements z of ρ for which ρϵz, will contain x but not y—which is impossible.

5 H. Vieler, loc. cit.

6 If the axiom of replacement is to be considered, read “I–VIII” and “II–VIII” throughout, instead of “I–VII” and “II–VII” respectively.

7 For reasons which will be clear, we employ xeΣ where, according to the system of notation of PM, we should write xϵΣ.

8 This definition is contained implicitly in our formulation of Axiom II.

9 {x} is a representative of the unit sets of x, of which there may exist more than one. Therefore if we ascribe any property to a set {x}, we ascribe implicitly the same property to any set equal to {x}.

10 We denote the relation of equality in Σ by = (,), that in Σ′ by = ′(,).

11 We use the abbreviation “y is an ϵ-member (ϵ-subset, ϵ′-membcr, etc.) of x,” instead of “y is a member (subset) of x within Σ (Σ′).”

12 See for example Skolem, Th., Über einige Grundlagenfragen der Mathematik, Skrifter utgitt av Det Norske Videnskaps-Akademi i Oslo, I. mat.-nat. kl., 1929, p. 3Google Scholar.

13 x ϕ is the ϵ-subset of x whose members are characterized by the property ϕ.

14 As a matter of fact, this can occur only when x ϕ is a null set within Σ′.

15 We denote by =″ (,) the relation of equality which is defined by Definition II within Σ′.