I. The present paper contains a formal proof of the following theorem of the elementary system ⊨ [ 1 0 ] c:

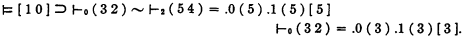
This theorem means that if there were a theorem of ⊢0 ( 3 2 ) 0 stating that there is no contradiction in ⊢2 ( 5 4 ) 2, we would have a contradiction in ⊢2 ( 5 4 ) 2. (This is in accordance with the second theorem of Gödel.)

Our proof is based on the calculus of the system ⊨ [ 1 0 ] c and of the metasystem ⊢0 ( 3 2 ) 0.

Note that we could take

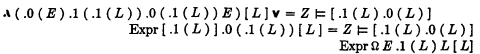
instead of Ax E .1 ( L ) (.1 ( L ) .0 ( L ) L) Z. We would then have to do with the simple systems and metasystems of Hetper, which do not contain propositional variables or the logico-semantical axiom. Our method applies equally to the systems and metasystems of New Foundation and to the simple systems and metasystems of Hetper.

Our proof can be considerably simplified by using a recent result of Hetper concerning ancestral functions. Hetper introduces the following abbreviations:

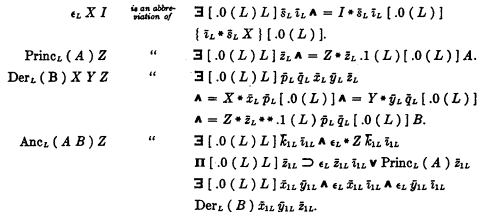
If A ( Z1c), B ( x1cy1cZ1c) are propositions, the expression 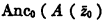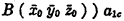will be called an ancestral function (we prove without difficulty that this expression is a proposition). The expressions 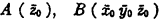will be called respectively the principal term and the term of derivation of this function.