In this paper the symbolism, definitions and results of my two papers, namely A test for the existence of tautologies according to many-valued truth-tables (hereafter referred to as ET) and Note on truth-tables (hereafter referred to as TT) will be presupposed.

The problem whether two arbitrary truth-tables with finite number of elements are equal or not was reduced in TT to the question of equality of two identical tables in which different elements have been designated. However, no general method for testing the equality of truth-tables was given there, although some cases were discussed for which such a method is available. In the present paper we shall describe a general method using the considerations of ET and TT.

In a series of five papers, Fitch has constructed a system of combinatory logic K′ which is adequate for much of classical analysis, and is demonstrably consistent if we assume the validity of transfinite induction up to a certain ordinal (at present undetermined). The system has the following peculiarities:

1.1. It is non-finitary, i.e. the class of Gödel-numbers of its theorems does not form the range of values of any recursive function (nor, as a matter of fact, of any function definable in elementary number theory).

1.2. It does not permit quantification over real numbers; i.e. it contains no theorems of the form

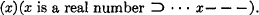
1.3. Because of 1.1, we cannot, except in trivial cases, construct actual proofs in K′; we have to resort to a metalanguage (of undetermined strength) in order to show that certain formulae are theorems of K′. Also because of 1.2, many important theorems of classical mathematics are not forthcoming in K′ itself, but only in the aforementioned metalanguage, e.g. in the form

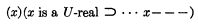
where ‘x’ is a syntactical rather than a numerical variable, a U-real is an expression of K′ rather than a number, and ‘ … x– – –’ ascribes a syntactical rather than a real number-theoretic property to x.

The purpose of this paper is to construct a finitary metalanguage for K′ in which all of Fitch's important theorems may be proved.

In this paper a theorem about numerical relations will be established and shown to have certain consequences concerning decidability in quantification theory, as well as concerning the foundation of number theory. The theorem is that relations of natural numbers are reducible in elementary fashion to symmetric ones; i.e.:

Theorem I. For every dyadic relation R of natural numbers there is a symmetric dyadic relation H of natural numbers such that R is definable in terms of H plus just truth-functions and quantification over natural numbers.

To state the matter more fully, there is a (well-formed) formula ϕ of pure quantification theory, or first-order functional calculus, which meets these conditions:

(a) ϕ has ‘x’ and ‘y’ as sole free individual variables;

(b) ϕ contains just one predicate letter, and it is dyadic;

(c) for every dyadic relation R of natural numbers there is a symmetric dyadic relation H of natural numbers such that, when the predicate letter in ϕ is interpreted as expressing H, ϕ comes to agree in truth-value with ‘x bears R to y’ for all values of ‘x’ and ‘y’.

In a current paper, Church and Quine show how any dyadic relation of natural numbers can be defined in terms of a symmetric dyadic relation of natural numbers together with the truth functions and quantification over natural numbers. The purpose of the present note is to extend their result to the following: Where R1, R2, …, ad infinitum are any classes or relations (of any degree) of natural numbers, they can all be defined in terms of a single symmetric dyadic relation of natural numbers together with the truth functions and quantification over natural numbers.

Let pi, for each i, be the tth prime > 1. Let the degree of Ri, for each i, be di. Let R be the dyadic relation which each number x bears to each number y such that either x is a factor of y or else x is 0 and y is for some such that . Since R is dyadic, we know from Church and Quine's result that R is definable in terms of a symmetric dyadic relation. Moreover, as seen in the incidental constructions in §1 of Church and Quine, ‘y = x + 1’ is expressible on the same basis.

The treatment of simplicity in my book and in earlier articles needs one important amplification and certain minor amendments. The basic method for computing complexity values nevertheless remains the same.

New studies show that so to adjust the actual technique of computation as to take full account of the factor of reflexivity would result in unwieldy rules. Fortunately, however, this is unnecessary; for the method already prescribed works for thoroughly irreflexive predicates, and every other predicate is replaceable by such predicates. Thus we need only require that before the complexity of a basis is evaluated every primitive be replaced by the simplest adequate set of irreflexive predicates.

Consider, for example, two-place predicates that are not irreflexive. Any two-place (or indeed any n-place) predicate that is satisfied only by identity pairs (or identity n-ads) can obviously be replaced by a one-place predicate. Any two-place predicate that is satisfied by some non-identity pairs and that is either exactly reflexive (i.e. satisfied also by just the identity pairs of elements in such non-identity pairs) or totally reflexive (i.e. satisfied also by all identity pairs) can be replaced by a two-place irreflexive predicate. In the former case, for instance, we replace “P” by “Q”, so explained that Qx, y if and only if Px, y and x ≠ y; and then define:

Finally, a non-irreflexive two-place predicate “P” that is of none of these three kinds can be replaced by a one-place and an irreflexive two-place predicate as follows:—let Qx if and only if Px,x, and let Rx,y if and only if Px,y andx ≠ y; then define:

Predicates of more than two places offer much greater variety since they may exhibit any sort of reflexivity with respect to any selection of places.

Martin has shown that the notions of ancestral and class-inclusion are sufficient to develop the theory of natural numbers in a system containing variables of only one type.

The purpose of the present paper is to show that an analogous construction is possible in a system containing, beyond the quantificational level, only the ancestral and the ordered pair.

The formulae of our system comprise quantificational schemata and anything which can be obtained therefrom by writing pairs (e.g. (x; y), ((x; y); (x; (y; y))) etc.) for free variables, or by writing ancestral abstracts (e.g. (*xyFxy) etc.) for schematic letters, or both.

The ancestral abstract (*xyFxy) means what is usually meant by ; and the formula (*xyFxy)zw answers to Martin's (zw; xy)(Fxy).

The system presupposes a non-simple applied functional calculus of the first order, with a rule of substitution for predicate letters; over and above this it has three axioms for the ancestral and two for the ordered pair.