Published online by Cambridge University Press: 12 March 2014
The treatment of simplicity in my book and in earlier articles needs one important amplification and certain minor amendments. The basic method for computing complexity values nevertheless remains the same.
New studies show that so to adjust the actual technique of computation as to take full account of the factor of reflexivity would result in unwieldy rules. Fortunately, however, this is unnecessary; for the method already prescribed works for thoroughly irreflexive predicates, and every other predicate is replaceable by such predicates. Thus we need only require that before the complexity of a basis is evaluated every primitive be replaced by the simplest adequate set of irreflexive predicates.
Consider, for example, two-place predicates that are not irreflexive. Any two-place (or indeed any n-place) predicate that is satisfied only by identity pairs (or identity n-ads) can obviously be replaced by a one-place predicate. Any two-place predicate that is satisfied by some non-identity pairs and that is either exactly reflexive (i.e. satisfied also by just the identity pairs of elements in such non-identity pairs) or totally reflexive (i.e. satisfied also by all identity pairs) can be replaced by a two-place irreflexive predicate. In the former case, for instance, we replace “P” by “Q”, so explained that Qx, y if and only if Px, y and x ≠ y; and then define:
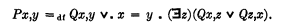
Finally, a non-irreflexive two-place predicate “P” that is of none of these three kinds can be replaced by a one-place and an irreflexive two-place predicate as follows:—let Qx if and only if Px,x, and let Rx,y if and only if Px,y andx ≠ y; then define:
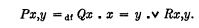
Predicates of more than two places offer much greater variety since they may exhibit any sort of reflexivity with respect to any selection of places.
1 The structure of appearance [hereinafter referred to as “SA”] (Cambridge, Mass., 1951), pp. 59–75Google Scholar; The logical simplicity of predicates, this Journal, vol. 14 (1949), pp. 32–41Google Scholar; and An improvement in the theory of simplicity, this Journal, vol. 14 (1949), pp. 228–229Google Scholar. Some points in the present paper were arrived at as the result of questions by my students Mr. A.N. Chomsky and Mr. H. C. Bohnert.
2 An n-place predicate is irreflexive if and only if it is satisfied only by sequences consisting of n different components. A one-place predicate is both reflexive and irrefiexive.
3 SA, p. 75.
4 SA, p. 70.
5 SA, pp. 74–75.