Schiller Joe Scroggs in [9] established remarkable facts concerning “normal” extensions of the modal sentential calculus S5, the most notable of these facts being that all such proper extensions have finite characteristic matrices. The major import of the present paper is that like facts hold for the relevant sentential calculus R-Mingle (RM). Robert K. Meyer in [6] has obtained an important completeness result for RM, which will play a central role in our results. However, in §2 we shall obtain a new proof of Meyer's result as a by-product of the algebraic logic that we develop in §1. Also in §2 we shall obtain the promised results for extensions of RM. In §3 we shall provide a strong completeness theorem for RM by generalizing the semantics of Meyer.

A theory formulated in a countable predicate calculus can have at most nonisomorphic countable models. It has been conjected (e.g., in [4]) that if it has an uncountable number of such models then it has exactly such. Of course, this would follow immediately if one assumed the continuum hypothesis.

In this paper we show that if a theory has more than ℵ1 (i.e., at least ℵ2) isomorphism types of countable models then it has exactly . Our results generalize immediately to theories in Lω1ω and even to pseudo-axiomatic classes in Lω1ω . In this last case, a result of H. Friedman shows that it is the best possible result.

The algebras studied in this paper were suggested to the author by William Craig as a possible substitute for cylindric algebras. Both kinds of algebras may be considered as algebraic versions of first-order logic. Cylindric algebras can be introduced as follows. Let ℒ be a first-order language, and let be an ℒ-structure. We assume that ℒ has a simple infinite sequence ν 0, ν 1, … of individual variables, and we take as known what it means for a sequence ν 0, ν 1, … of individual variables, and we take as known what it means for a sequence x = 〈x 0, x 1, …〉 of elements of to satisfy a formula ϕ of ℒ in . Let ϕ be the collection of all sequences x which satisfy ϕ in . We can perform certain natural operations on the sets ϕ , of basic model-theoretic significance: Boolean operations = cylindrifications diagonal elements (0-ary operations) . In this way we make the class of all sets ϕ into an algebra; a natural abstraction gives the class of all cylindric set algebras (of dimension ω). Thus this method of constructing an algebraic counterpart of first-order logic is based upon the notion of satisfaction of a formula by an infinite sequence of elements. Since, however, a formula has only finitely many variables occurring in it, it may seem more natural to consider satisfaction by a finite sequence of elements; then ϕ becomes a collection of finite sequences of varying ranks (cf. Tarski [10]). In forming an algebra of sets of finite sequences it turns out to be possible to get by with only finitely many operations instead of the infinitely many ci 's and dij 's of cylindric algebras. Let be the class of all algebras of sets of finite sequences (an exact definition is given in §1).

Martin [4, Theorems 1 and 2] proved that a Turing degree a is the degree of a maximal set if, and only if, a′ = 0″. Lachlan has shown that maximal sets have minimal many-one degrees [2, §1] and that every nonrecursive r.e. Turing degree contains a minimal many-one degree [2, Theorem 4]. Our aim here is to show that any r.e. Turing degree a of a maximal set contains an infinite number of maximal sets whose many-one degrees are pairwise incomparable; hence such Turing degrees contain an infinite number of distinct minimal many-one degrees. This theorem has been proved by Yates [6, Theorem 5] in the case when a = 0′.

The need for this theorem first came to our attention as a result of work done by the author [3, Theorem 2.3]. There we looked at the structure / obtained from the recursive functions of one variable under the equivalence relation f ~ g if, and only if, f(x) = g(x) a.e., that is, for all but finitely many x ∈ , where M is a maximal set, and M is its complement. We showed that / 1 ≡ / 2 if, and only if, 1 = m 2, i.e., 1. and 2 have the same many-one degree. However, it might be possible that some Turing degree of a maximal set contains exactly one many-one degree of a maximal set. Theorem 1 was proved to show that this was not the case, and hence that the theory of / is not an invariant of Turing degree.

A set S of degrees is said to be an initial segment if c ≤ d ∈ S→-c∈S. Shoenfield has shown that if P is the lattice of all subsets of a finite set then there is an initial segment of degrees isomorphic to P. Rosenstein [2] (independently) proved the same to hold of the lattice of all finite subsets of a countable set. We shall show that “countable set” may be replaced by “set of cardinality at most that of the continuum.” This result is also an extension of [3, Corollary 2 to Theorem 15], which states that there is a sublattice of degrees isomorphic to the lattice of all finite subsets of 2 N . (A sublattice of degrees is a subset closed under ∪ and ∩; an initial segment closed under ∪ is necessarily a sublattice, but not conversely.)

It seems worth noting that the proof of the present result was preceded in time by our proof [4] of the analogous theorem for hyperdegrees, and is in fact an adaptation of that proof. Thus the present work has been influenced much more directly by the Gandy-Sacks forcing construction of a minimal hyperdegree [1] than by previous work on initial segments of degrees.

In [1], Sacks points out that there is one fundamental question: which true statements of ordinary recursion theory remain true when appropriately extended to metarecursion theory?

A particular interest is taken in the question [1]:

Q6. How does one define the jump operator for metarecursion theory? (A satisfactory definition should have the property that if A is metarecursive in B, then the jump of A is metarecursive in the jump of B.)

In [2], Kreisel and Sacks give some definitions of predicates and functions analogous to those of Kleene as follows:

The T-predicate of [2] is analogous to that of Kleene [3]. Its definition is

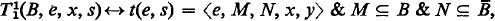
where e is the Gödel number of a finite system of equations E and t(e, s) is a special metarecursive function which indexes “deductions” from E.

U(e, s) is a metarecursive function such that if t(e, s) = 〈e, M, N, x, y〉, then U(e,s) = y.

Two partial functions {e} s and {e} are

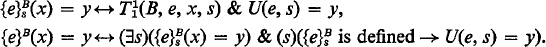
Then e is intrinsically consistent if for all x, s 1 and s 2, if t(e, S 1) = 〈e, M 1 N 1, x, y 1〉, t(e, s 2) = 〈e, M 2, N 2, x, y 2〉 and (M 1 ∪ M 2) ∩ (N 1 ∪ N 2) = ∅, then y 1 = y 2.

Recursive equivalence types are an effective or recursive analogue of cardinal numbers. They were introduced by Dekker in the early 1950's. The richness of various theories related to the recursive equivalence types is demonstrated in this paper by showing that the theory of any countable relational structure can be embedded in or interpreted in these theories. A more complete summary is presented in the last paragraph of this section.

Let E = {0,1, 2, …} be the natural numbers. If α ⊆ E, β ⊆ E, and there is a 1-1 partial recursive function f such that the image under f of α is β, α and β are called recursively equivalent (see [3]). The recursive equivalence type or RET of α, denoted 〈α〉, is the class of all β recursively equivalent to α. Addition of RETs is defined by 〈α〉 + 〈β〉 = 〈{2x ∣ x ∈ α} ∪ 〈{2x + 1 ∣ x ∈ β}〉. The partial ordering ≤ is defined on the RETs by A ≤ B iff (EC)(A + C = B). An RET, X, is called an isol if X ≠ X + 1 or, equivalently, if no representative of X is recursively equivalent to a proper subset of itself. The isols are thus the recursive analogue of the Dedekind-finite cardinals.

If X is a set, [Χ] ω will denote the set of countably infinite subsets of X. ω is the set of natural numbers. If S is a subset of [ω] ω , we shall say that S is Ramsey if there is some infinite subset X of ω such that either [Χ] ω ⊆ S or [Χ] ω ∩ S = 0. Dana Scott (unpublished) has asked which sets, in terms of logical complexity, are Ramsey.

The principal theorem of this paper is: Every Σ 1 1 (i.e., analytic) subset of [ω] ω is Ramsey (for the Σ, Π notations, see Addison [1]). This improves a result of Galvin-Prikry [2] to the effect that every Borel set is Ramsey. Our theorem is essentially optimal because, if the axiom of constructibility is true, then Gödel's Σ2 1 Π2 1 well-ordering of the set of reals [3], having the convenient property that the set of ω-sequences of reals enumerating initial segments is also Σ2 1 ∩ Π2 1, rather directly gives a Σ2 1 ∩ Π2 1 set which is not Ramsey. On the other hand, from the assumption that there is a measurable cardinal we shall derive the conclusion that every Σ 2 1 (i.e., PCA) is Ramsey. Also, we shall explore the connection between Martin's axiom and the Ramsey property.

Let be a version of class set theory admitting urelemente, and with AC (= axiom of choice) replaced by AC0 (= axiom of choice for sets of finite sets), ω = nonnegative integers, and Δ = Dedekind cardinals. Let be an arbitrarily quantified positive first order sentence in functors for + and ·. Let ƒ0, … , ƒ κ - 1 be function variables and the universal sentence obtained from by replacing existential quantifiers by the ƒ1 as Skolem functions.

Morley conjectured that if an infinite first-order theory T is categorical in the power |T| > ℵ0, then it has a model of power < |T| Here we affirm this conjecture for the case |T|ℵ0=|T|.

We shall prove that if is an ultrafilter and λ ℵ0 = λ. This affirms a conjecture of Keisler.

This paper is based on the notions originally described by Dekker [2], [3], and the reader is referred to these for explanation of notation etc. Briefly, we are concerned with a countably infinite dimensional countable vector space Ū with recursive operations, regarded as being coded as a set of natural numbers. Necessarily, then, Ū must be a vector space over a field which itself is in some sense recursively enumerable and has recursive operations.

Two cardinals are said to be indistinguishable if there is no sentence of second order logic which discriminates between them. This notion, which is defined precisely below, is closely related to that of characterizable cardinals, introduced and studied by Garland in [3]. In this paper we give an algebraic criterion for two cardinals to be indistinguishable. As a consequence we obtain a straightforward proof of an interesting theorem about characterizable cardinals due to Zykov [6].

Prior has conjectured that the tense-logical system Gli obtained by adding to a complete basis for the classical propositional calculus the primitive symbol G, the definitions

Df. F: Fα = NGNα

Df. L: Lα = KαGα,

and the postulates

is complete for the logic of linear, infinite, transitive, discrete future time. In this paper it is demonstrated that that conjecture is correct and it is shown that Gli has the finite model property: see [4]. The techniques used are in part suggested by those used in Bull [2] and [3]:

Gli can be shown to be complete for the logic of linear, infinite, transitive, discrete future time in the sense that every formula of Gli which is true of such time can be proved as a theorem of Gli. For this purpose the notion of truth needs to be formalized. This formalization is effected by the construction of a model for linear, infinite, transitive, discrete future time.

J. N. Crossley [1] raised the question of whether the implication 2 + A = A ⇒ 1 + A = A is true for constructive order types (C.O.T.'s). Using an earlier definition of constructive order type, A. G. Hamilton [2] presented a counterexample. Hamilton left open the general question, however, since he pointed out that Crossley considers only orderings which can be embedded in a standard dense r.e. ordering by a partial recursive function, and that his counterexample fails to meet this requirement. We resolve the question by finding a C.O.T. A which meets Crossley's requirement and such that 2 + A = A but 1 + A ≠ A. At the suggestion of A. B. Manaster and A. G. Hamilton we easily extend this construction to show that for any n ≧ 2, there is a C.O.T. A such that n + A = A but m + A ≠ A for 0 < m < n. Hence, Theorem 3 of [2] and all of its corollaries hold with the new definition of C.O.T. The construction is not difficult and requires no priority argument. The techniques are similar to those developed in [3], but no outside results are needed here.