The algebras studied in this paper were suggested to the author by William Craig as a possible substitute for cylindric algebras. Both kinds of algebras may be considered as algebraic versions of first-order logic. Cylindric algebras can be introduced as follows. Let ℒ be a first-order language, and let 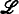be an ℒ-structure. We assume that ℒ has a simple infinite sequence ν 0, ν 1, … of individual variables, and we take as known what it means for a sequence ν 0, ν 1, … of individual variables, and we take as known what it means for a sequence x = 〈x 0, x 1, …〉 of elements of 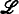to satisfy a formula ϕ of ℒ in 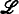. Let ϕ 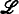be the collection of all sequences x which satisfy ϕ in 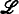. We can perform certain natural operations on the sets ϕ 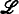, of basic model-theoretic significance: Boolean operations =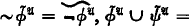 cylindrifications 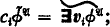diagonal elements (0-ary operations) 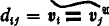. In this way we make the class of all sets ϕ 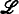into an algebra; a natural abstraction gives the class 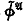of all cylindric set algebras (of dimension ω). Thus this method of constructing an algebraic counterpart of first-order logic is based upon the notion of satisfaction of a formula by an infinite sequence of elements. Since, however, a formula has only finitely many variables occurring in it, it may seem more natural to consider satisfaction by a finite sequence of elements; then ϕ 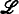becomes a collection of finite sequences of varying ranks (cf. Tarski [10]). In forming an algebra of sets of finite sequences it turns out to be possible to get by with only finitely many operations instead of the infinitely many ci 's and dij 's of cylindric algebras. Let 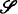be the class of all algebras of sets of finite sequences (an exact definition is given in §1).