Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T07:00:21.498Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost combinatorial Skolem functions

Published online by Cambridge University Press:  12 March 2014

Erik Ellentuck
Erik Ellentuck*
Affiliation:
Rutgers, The State University and Kyoto University
Get access Rights & Permissions [Opens in a new window]

Extract

Let be a version of class set theory admitting urelemente, and with AC (= axiom of choice) replaced by AC0 (= axiom of choice for sets of finite sets), ω = nonnegative integers, and Δ = Dedekind cardinals. Let 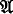be an arbitrarily quantified positive first order sentence in functors for + and ·. Let ƒ0, … , ƒ κ - 1 be function variables and 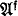the universal sentence obtained from 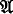by replacing existential quantifiers by the ƒ1 as Skolem functions.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 35 , Issue 1 , March 1970 , pp. 65 - 72
Copyright
Copyright © Association for Symbolic Logic 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The author is deeply indebted to Professors J. Myhill (A. Nerode), the inventors of combinatorial (almost combinatorial) functions for their long standing encouragement. He would also like to thank Professor H. Yoshizawa and the staff of Kyoto University for all their help. This paper was prepared while the author was supported by a New Jersey Research Council Faculty Fellowship.

References

[1] Ellentuck, E., The universal properties of Dedekind finite cardinals, Annals of mathematics, vol. 82 (1965), pp. 225–248.CrossRefGoogle Scholar
[2] Ellentuck, E., The representation of cardinals in models of set theory, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 84–99.CrossRefGoogle Scholar
[3] Ellentuck, E., The first order properties of Dedekind finite integers, Fundamenta mathematicae, vol. 63 (1968), pp. 7–25.CrossRefGoogle Scholar
[4] Ellentuck, E., A choice free theory of Dedekind cardinals, this Journal, vol. 34 (1969), pp. 70–84.Google Scholar
[5] Ellentuck, E., Extension methods in cardinal arithmetic, Transactions of the American Mathematical Society (to appear).Google Scholar
[6] Gauntt, R. J., Undefinability of cardinality, Summer Institute on Axiomatic Set Theory, University of California, Los Angeles, Calif., 1967.Google Scholar
[7] Qödel, K., The consistency of the continuum hypothesis, Princeton Univ. Press, Princeton, N.J., 1940.Google Scholar
[8] Mostowski, A., Über die Unabhängigkeit des Wohlordnungssatzes vom Ordnungsprinzip, Fundamenta mathematicae, vol. 32 (1939), pp. 201–252.CrossRefGoogle Scholar
[9] Shoenheld, J., The problem of predicativity in Essays on the foundations of mathematics, Magnus Press, Hebrew University, Jerusalem, 1961, pp. 132–139.Google Scholar