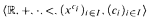Research Article
On the existence of Stone-Čech compactification
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1137-1146
-
- Article
- Export citation
Generalizations of small profinite structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1147-1175
-
- Article
- Export citation
Directed free pseudospaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1176-1198
-
- Article
- Export citation
Formalizing non-standard arguments in second-order arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1199-1210
-
- Article
- Export citation
Stable types in rosy theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1211-1230
-
- Article
- Export citation
PCF structures of height less than ω3
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1231-1248
-
- Article
- Export citation
The reducts of equality up to primitive positive interdefinability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1249-1292
-
- Article
- Export citation
Dual Borel Conjecture and Cohen reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1293-1310
-
- Article
- Export citation
Expansions of the real field by open sets: definability versus interpretability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1311-1325
-
- Article
- Export citation
Consistency of strictly impredicative NF and a little more …
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1326-1338
-
- Article
- Export citation
A high c.e. degree which is not the join of two minimal degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1339-1358
-
- Article
- Export citation
A Note on Hjorth's oscillation theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1359-1365
-
- Article
- Export citation
Infinite substructure lattices of models of Peano Arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1366-1382
-
- Article
- Export citation
Diagonal Prikry extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1383-1402
-
- Article
- Export citation
A co-analytic maximal set of orthogonal measures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1403-1414
-
- Article
- Export citation
The characteristic sequence of a first-order formula
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1415-1440
-
- Article
- Export citation
Uniform model-completeness for the real field expanded by power functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1441-1461
-
- Article
- Export citation
Grouplike minimal sets in ACFA AND in TA
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1462-1488
-
- Article
- Export citation
The full binary tree cannot be interpreted in a chain
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1489-1498
-
- Article
- Export citation
Front matter
JSL volume 75 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation

 of (ℝ, +, ·), every subset of ℝ definable in (
of (ℝ, +, ·), every subset of ℝ definable in (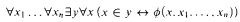
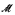 of Peano Arithmetic has a cofinal elementary extension
of Peano Arithmetic has a cofinal elementary extension 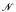 such that the interstructure lattice Lt(
such that the interstructure lattice Lt( maximal orthogonal (i.e., mutually singular) set of measures on Cantor space. This provides a natural counterpoint to the well-known theorem of Preiss and Rataj [16] that no analytic set of measures can be maximal orthogonal.
maximal orthogonal (i.e., mutually singular) set of measures on Cantor space. This provides a natural counterpoint to the well-known theorem of Preiss and Rataj [16] that no analytic set of measures can be maximal orthogonal.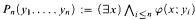 . We show that combinatorial and classification theoretic properties of the characteristic sequence reflect classification theoretic properties of
. We show that combinatorial and classification theoretic properties of the characteristic sequence reflect classification theoretic properties of