Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T22:40:14.602Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions of the real field by open sets: definability versus interpretability

Published online by Cambridge University Press:  12 March 2014

Harvey Friedman ,
Krzysztof Kurdyka ,
Chris Miller  and
Patrick Speissegger
Harvey Friedman
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue Columbus. Ohio 43210., USA. E-mail: [email protected]
Krzysztof Kurdyka
Affiliation:
Laboratoire de Mathématiques, Université de Savoie, UMR 5127 CNRS, 73376 Le Bourget-Du-Lac, France. E-mail: [email protected]
Chris Miller
Affiliation:
Department of Mathematics, The Ohio State University, 231 West 18th Avenue Columbus, Ohio 43210, USA. E-mail: [email protected]
Patrick Speissegger
Affiliation:
Department of Mathematics & Statistics, McMaster University, 1280 Main Street West Hamilton, Ontario L8S 4K1, Canada. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An open U ⊆ ℝ is produced such that (ℝ, +, ·, U) defines a Borel isomorph of (ℝ, +, ·, ℕ) but does not define ℕ. It follows that (ℝ, +, ·, U) defines sets in every level of the projective hierarchy but does not define all projective sets. This result is elaborated in various ways that involve geometric measure theory and working over o-minimal expansions of (ℝ, +, ·). In particular, there is a Cantor set E ⊆ ℝ such that (ℝ, +, ·, ℕ) defines a Borel isomorph of (ℝ, +, ·, ℕ) and, for every exponentially bounded o-minimal expansion 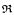of (ℝ, +, ·), every subset of ℝ definable in (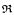, E) either has interior or is Hausdorff null.

Keywords

expansion of the real fieldo-minimalprojective hierarchyCantor setHausdorff dimensionMinkowski dimension
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 4 , December 2010 , pp. 1311 - 1325
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Dougherty, Randall and Miller, Chris, Definable Boolean combinations of open sets are Boolean combinations of open definable sets, Illinois Journal of Mathematics, vol. 45 (2001), no. 4, pp. 1347–1350.CrossRefGoogle Scholar
[2]Friedman, Harvey and Miller, Chris, Expansions of o-minimal structures by sparse sets, Fundamenta Mathematicae, vol. 167 (2001), no. 1, pp. 55–64.CrossRefGoogle Scholar
[3]Friedman, Harvey and Miller, Chris, Expansions of o-minimal structures by fast sequences, this Journal, vol. 70 (2005), no. 2, pp. 410–418.Google Scholar
[4]Gelbaum, Bernard R. and Olmsted, John M. H., Counterexamples in analysis, Dover Publications Inc., Mineola, NY, 2003, corrected reprint of the second (1965) edition.Google Scholar
[5]Hieronymi, Philipp, Defining the set of integers in expansions of the real field by a closed discrete set, Proceedings of the American Mathematical Society, posted on February 2. 2010. PII S 0002-9939(10)10268-8 (to appear in print).Google Scholar
[6]Kechris, Alexander S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.CrossRefGoogle Scholar
[7]Lion, Jean-Marie, Miller, Chris, and Speissegger, Patrick, Differential equations over polynomially bounded o-minimal structures, Proceedings of the American Mathematical Society, vol. 131 (2003), no. 1, pp. 175–183 (electronic).CrossRefGoogle Scholar
[8]Mattila, Pertti, Geometry of sets and measures in Euclidean spaces, Cambridge Studies in Advanced Mathematics, vol. 44, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[9]Miller, Chris, Exponentiation is hard to avoid, Proceedings of the American Mathematical Society, vol. 122 (1994), no. 1, pp. 257–259.CrossRefGoogle Scholar
[10]Miller, Chris, Tameness in expansions of the real field, Logic Colloquium '01, Lecture Notes in Logic, vol. 20, Association for Symbolic Logic, Urbana, IL, 2005, pp. 281–316.CrossRefGoogle Scholar
[11]Miller, Chris, Avoiding the projective hierarchy in expansions of the real field by sequences, Proceedings of the American Mathematical Society, vol. 134 (2006), no. 5, pp. 1483–1493 (electronic).CrossRefGoogle Scholar
[12]Miller, Chris and Speissegger, Patrick, Expansions of the real line by open sets: o-minimality and open cores, Fundamenta Mathematicae, vol. 162 (1999), no. 3, pp. 193–208.Google Scholar
[13]Miller, Chris and Tyne, James, Expansions of o-minimal structures by iteration sequences, Notre Dame Journal of Formal Logic, vol. 47 (2006), no. 1, pp. 93–99 (electronic).CrossRefGoogle Scholar
[14]Speissegger, Patrick, The Pfaffian closure of an o-minimal structure. Journal für die Reine und Angewandte Mathematik, vol. 508 (1999), pp. 189–211.CrossRefGoogle Scholar
[15]van den Dries, Lou, Dense pairs of o-minimal structures, Fundamenta Mathematicae, vol. 157 (1998), no. 1, pp. 61–78.CrossRefGoogle Scholar
[16]van den Dries, Lou, Tame topology and o-minimal structures, London Mathematical Society Lecture Note Series, vol. 248, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
[17]van den Dries, Lou and Miller, Chris, Geometric categories and o-minimal structures, Duke Mathematical Journal, vol. 84 (1996), no. 2, pp. 497–540.CrossRefGoogle Scholar
[18]Yomdin, Yosef and Comte, Georges, Tame geometry with application in smooth analysis, Lecture Notes in Mathematics, vol. 1834, Springer-Verlag, Berlin, 2004.CrossRefGoogle Scholar