Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T20:46:27.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Consistency of strictly impredicative NF and a little more …

Published online by Cambridge University Press:  12 March 2014

Sergei Tupailo
Sergei Tupailo*
Affiliation:
Centro de Matemática e Aplicações Fundamentais, Universidade de Lisboa, Avenida Professor Gama Pinto 2, 1649-003 Lisboa, Portugal. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An instance of Stratified Comprehension

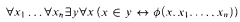
is called strictly impredicative iff, under minimal stratification, the type of x is 0. Using the technology of forcing, we prove that the fragment of NF based on strictly impredicative Stratified Comprehension is consistent. A crucial part in this proof, namely showing genericity of a certain symmetric filter, is due to Robert Solovay.

As a bonus, our interpretation also satisfies some instances of Stratified Comprehension which are not strictly impredicative. For example, it verifies existence of Frege natural numbers.

Apparently, this is a new subsystem of NF shown to be consistent. The consistency question for the whole theory NF remains open (since 1937).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 4 , December 2010 , pp. 1326 - 1338
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Boffa, M., ZFJ and the consistency problem for NF, Jahrbuch der Kurt Gödel Gesellschaft, vol. 1 (1988), pp. 102–106.Google Scholar
[2]Crabbé, M., On the consistency of an impredicative subsystem of Quine's NF, this Journal, vol. 47 (1982), pp. 131–136.Google Scholar
[3]Forster, T. E., Set theory with a universal set, second ed., The Clarendon Press, Oxford, 1995.CrossRefGoogle Scholar
[4]Hailperin, T., A set of axioms for logic, this Journal, vol. 9 (1944), pp. 1–19.Google Scholar
[5]Holmes, M. R., Subsystems of Quine's “New Foundations” with predicativity restrictions, Notre Dame Journal of Formal Logic, vol. 40 (1999), no. 2, pp. 183–196.CrossRefGoogle Scholar
[6]Jech, T., Set theory, the Third Millennium ed., Springer-Verlag, 2002.Google Scholar
[7]Jensen, R. B., On the consistency of a slight(?) modification of Quine's NF, Synthese, vol. 19 (1969), pp. 250–263.CrossRefGoogle Scholar
[8]Kunen, K., Set theory. An introduction to independence proofs, Elsevier, 1980.Google Scholar
[9]Quine, W. V., New Foundations for Mathematical Logic, The American Mathematical Monthly, vol. 44 (1937), pp. 70–80.CrossRefGoogle Scholar
[10]Specker, E. P., Typical ambiguity, Logic, Methodology and Philosophy of Science (Nagel, E., editor), Stanford University Press, Stanford, California, 1962, pp. 116–124.Google Scholar
[11]Tupailo, S., Monotone inductive definitions and consistency of New Foundations, Proceedings of logic Colloquium 2005 (Dimitracopoulos, C., Newelski, L., Normann, D., and Steel, J. R., editors), Lecture Notes in Logic, vol. 28, Cambridge University Press, 2008, pp. 255–272.Google Scholar
[12]Tupailo, S., NF and indiscernables in ZF, Proceedings of the 70th anniversary NF meeting in Cambridge (Crabbé, M. and Forster, T., editors), Cahiers du Centre de logique, vol. 16, Academia-Bruylant, Louvain-la-Neuve (Belgique), 2009, pp. 99–107.Google Scholar