Published online by Cambridge University Press: 12 March 2014
A set D of natural numbers is called Diophantine if it can be defined in the form
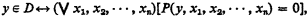
where P is a polynomial with integer coefficients. Recently, Ju. V. Matijasevič [2], [3] has shown that all recursively enumerable sets are Diophantine. From this, it follows that a bound for n may be given.
We use throughout the logical symbols ∧ (and), ∨ (or), → (if … then …), ↔ (if and only if), ⋀ (for every), and ⋁ (there exists); negation does not occur explicitly. The variables range over the natural numbers 0,1,2,3, …, except as otherwise noted.
It is the purpose of this paper to show that if we do not insist on prenex form, then every Diophantine set can be defined existentially by a formula in which not more than five existential quantifiers are nested. Besides existential quantifiers, only conjunctions are needed. By Matijasevič [2], [3], the representation extends to all recursively enumerable sets. Using this, we can find a bound for the number of conjuncts needed.
Davis [1] proved that every recursively enumerable set of natural numbers can be represented in the form
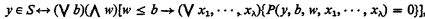
where P is a polynomial with integer coefficients. I showed in [5] that we can take λ = 4. (A minor error is corrected in an Appendix to this paper.) By the methods of the present paper, we can again obtain this result, and indeed in a stronger form, with the universal quantifier replaced by a conjunction.
Presented to the Fourth International Congress for Logic, Methodology and Philosophy of Science, in Bucharest, Romania, on September 3, 1971, under the title An undecidable Diophantine problem.