Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T22:03:57.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Proper forcing and remarkable cardinals II

Published online by Cambridge University Press:  12 March 2014

Ralf-Dieter Schindler
Ralf-Dieter Schindler*
Affiliation:
Institut für Formale Logik, Universität Wien, 1090 Wien, Austria, E-mail: [email protected], URL: http://www.logic.univie.ac.at/~rds/
Get access Rights & Permissions [Opens in a new window]

Abstract

The current paper proves the results announced in [5].

We isolate a new large cardinal concept, “remarkability.” Consistencywise, remarkable cardinals are between ineffable and ω-Erdös cardinals. They are characterized by the existence of “0#-like” embeddings; however, they relativize down to L. It turns out that the existence of a remarkable cardinal is equiconsistent with L(ℝ) absoluteness for proper forcings. In particular, said absoluteness does not imply 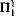determinacy.

Keywords

set theory/descriptive set theory/proper forcing/large cardinals
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 3 , September 2001 , pp. 1481 - 1492
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beller, A., Jensen, R., and Welch, Ph., Coding the universe, Cambridge, 1982.CrossRefGoogle Scholar
[2]Jech, T., Set theory, 1978, San Diego.Google Scholar
[3]Neeman, I. and Zapletal, J., Proper forcing and L(ℝ), preprint.Google Scholar
[4]Neeman, I. and Zapletal, J., Proper forcing and absoluteness in L(ℝ), Commentationes Mathematical Universitatis Carolinae, vol. 39 (1998), pp. 281–301.Google Scholar
[5]Schindler, R.-D., Proper forcing and remarkable cardinals, The Bulletin of Symbolic Logic, vol. 6 (2000), pp. 176–184.CrossRefGoogle Scholar
[6]Schindler, R.-D., Coding into K by reasonable forcing, Transactions of the American Mathematical Society, vol. 353 (2001), pp. 479–489.CrossRefGoogle Scholar
[7]Shelah, S., Proper forcing, Springer-Verlag, 1982.CrossRefGoogle Scholar
[8]Shelah, S. and Stanley, L., Coding and reshaping when there are no sharps, Set theory of the continuum (Judah, H.et al., editor), Springer-Verlag, 1992, pp. 407–416.CrossRefGoogle Scholar
[9]Steel, J., Core models with more Woodin cardinals, preprint.Google Scholar