The Jensen covering lemma says that either L has a club class of indiscernibles, or else, for every uncountable set A of ordinals, there is a set B ∈ L with A ⊆ B and card (B) = card(A). One might hope to extend Jensen's covering lemma to richer core models, which for us will mean to inner models of the form L[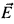 ] where
] where 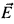 is a coherent sequence of extenders of the kind studied in Mitchell-Steel [8], The papers [8], [12], [10] and [1] show how to construct core models with Woodin cardinals and more. But, as Prikry forcing shows, one cannot expect too direct a generalization of Jensen's covering lemma to core models with measurable cardinals.
is a coherent sequence of extenders of the kind studied in Mitchell-Steel [8], The papers [8], [12], [10] and [1] show how to construct core models with Woodin cardinals and more. But, as Prikry forcing shows, one cannot expect too direct a generalization of Jensen's covering lemma to core models with measurable cardinals.
Recall from [8] that if L[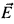 ] is a core model and α is an ordinal, then either Eα = ∅, or else Eα is an extender over
] is a core model and α is an ordinal, then either Eα = ∅, or else Eα is an extender over 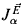 As in [8], we assume here that if Eα is an extender, then Eα is below superstrong type in the sense that the set of generators of Eα is bounded in
As in [8], we assume here that if Eα is an extender, then Eα is below superstrong type in the sense that the set of generators of Eα is bounded in 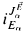 (crit(Eα)). Let us say that L[
(crit(Eα)). Let us say that L[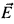 ] is a lower-part core model iff for every ordinal α, Eα is not a total extender over L[
] is a lower-part core model iff for every ordinal α, Eα is not a total extender over L[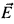 ]. In other words, if L[
]. In other words, if L[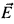 ] is a lower-part core model, then no cardinal in L[
] is a lower-part core model, then no cardinal in L[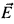 ] is measurable as witnessed by an extender on
] is measurable as witnessed by an extender on 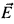 . Other than the “below superstrong” hypothesis, we impose no bounds on the large cardinal axioms true in the levels of a lower-part core model.
. Other than the “below superstrong” hypothesis, we impose no bounds on the large cardinal axioms true in the levels of a lower-part core model.
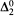 -spectrum of a linear order
-spectrum of a linear order