Hybrid languages are expansions of propositional modal languages which can refer to (or even quantify over) worlds. The use of strong hybrid languages dates back to at least [Pri67], but recent work (for example [BS98, BT98a, BT99]) has focussed on a more constrained system called H(↓, @). We show in detail that (↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that (↓, @) corresponds to the fragment of first-order logic which is invariant for generated submodels. We then show that (↓, @) enjoys (strong) interpolation, provide counterexamples for its finite variable fragments, and show that weak interpolation holds for the sublanguage (@). Finally, we provide complexity results for (@) and other fragments and variants, and sharpen known undecidability results for (↓, @).

We give a sound and complete axiomatization for the full computation tree logic. CTL*, of R-generable models. This solves a long standing open problem in branching time temporal logic.

The purpose of this paper is to present a kind of boundedness lemma for direct limits of coarse structural mice, and to indicate some applications to descriptive set theory. For instance, this allows us to show that under large cardinal or determinacy assumptions there is no prewellorder ≤ of length such that for some formula ψ and parameter z

if and only if

It is a peculiar experience to write up a result in this area. Following the work of Martin, Steel, Woodin, and other inner model theory experts, there is an enormous overhang of theorems and ideas, and it only takes one wandering pebble to restart the avalanche. For this reason I have chosen to center the exposition around the one pebble at 1.7 which I believe to be new. The applications discussed in section 2 involve routine modifications of known methods.

A detailed introduction to many of the techniques related to using the Martin-Steel inner model theory and Woodin's free extender algebra is given in the course of [1]. Certainly a familiarity with the Martin-Steel papers, [5] and [6], is a prerequisite, as is some knowledge of the free extender algebra. Probably anyone interested in this paper will already know the necessary descriptive set theory, most of which can be found in [4]. Discussion of earlier results in this direction can be found in [3] or [2].

In this paper first order theories for nonmonotone inductive definitions are introduced, and a proof-theoretic analysis for such theories based on combined operator forms à la Richter with recursively inaccessible and Mahlo closure ordinals is given.

We consider the following question of Kunen:

Does Con(ZFC + ∃M a transitive inner model and a non-trivial elementary embedding j: M → V)

imply Con(ZFC + ∃ a measurable cardinal)?

We use core model theory to investigate consequences of the existence of such a j: M → V. We prove, amongst other things, the existence of such an embedding implies that the core model K is a model of “there exists a proper class of almost Ramsey cardinals”. Conversely, if On is Ramsey, then such a j. M are definable.

We construe this as a negative answer to the question above. We consider further the consequences of strengthening the closure assumption on j to having various classes of fixed points.

Let G be an infinite abelian p-group and let K be a field of characteristic ≠ p. Let K[G] be the set of all sums Σg∈Gagg where the ag are in K, and all but finitely many ag are 0. Then K[G] is a K-algebra, with multiplication induced by the group multiplication on G.

If G is countable, then the isomorphism type of K[G] has been completely described by S. D. Berman [1]. If G is a direct sum of countable groups, one can also describe K[G], as K[⊕iGi] ≃ ⊗iK[Gi]. If K contains all pn-th roots of unity, then K[G] is isomorphic to the ring of continuous functions from a Boolean space X to the field K with the discrete topology. In that case, the group UK[G] of invertible elements of K[G] is isomorphic to the direct sum of ∣G∣ copies of K×. More generally, if K is of the second kind with respect to p (see below for the definition), the group UK[G] has a simple description.

Consider the subgroup SK[G] of elements Σgagg which have order a power of p and such that Σg ag = 1. This group is of course much simpler than UK[G]. Classifying SK[G] up to isomorphism reduces to the case where G has no element of infinite height, see [7]. If G is a direct sum of cyclic groups then the isomorphism type of SK[G] has been completely determined, in [2, 3, 7, 8]. The aim of this note is to show that a similar result is in general not possible for uncountable G. We use an invariant Γ associated to abelian groups, and for any regular uncountable cardinal κ, exhibit 2κ groups G for which Γ(G) = Γ(SK[G]) are pairwise distinct. Our work is based on a construction of Shelah [9], who constructed 2κ non-isomorphic abelian p-groups of cardinality κ for κ an uncountable regular cardinal.

We give a proof, valid in any elementary topos, of the theorem of Zermelo that any set possessing a choice function for its set of inhabited subsets can be well-ordered. Our proof is considerably simpler than existing proofs in the literature and moreover can be seen as a direct generalization of Zermelo's own 1908 proof of his theorem.

Let M be an L-structure and A be an infinite subset of M. Two structures can be defined from A:

• The induced structure on A has a name Rφ for every ∅-definable relation φ(M) ∩ An on A. Its language is

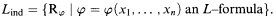
A with its Lind-structure will be denoted by Aind.

• The pair (M, A) is an L(P)-structure, where P is a unary predicate for A and L(P) = L ∪{P}.

We call A small if there is a pair (N, B) elementarily equivalent to (M, A) and such that for every finite subset b of N every L–type over Bb is realized in N.

A formula φ(x, y) has the finite cover property (f.c.p) in M if for all natural numbers k there is a set of φ–formulas

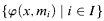
which is k–consistent but not consistent in M. M has the f.c.p if some formula has the f.c.p in M. It is well known that unstable structures have the f.c.p. (see [6].) We will prove the following two theorems.

Theorem A. Let A be a small subset of M. If M does not have the finite cover property then, for every λ ≥ ∣L∣, if both M andAindare λ–stable then (M, A) is λ–stable.

Corollary 1.1 (Poizat [5]). If M does not have the finite cover property and N ≺ M is a small elementary substructure, then (M, N) is stable.

Corollary 1.2 (Zilber [7]). If U is the group of wots of unity in the field ℂ of complex numbers the pair (ℂ, U) isω–stable.

Proof. (See [4].) As a strongly minimal set ℂ is ω–stable and does not have the f.c.p. By the subspace theorem of Schmidt [3] every algebraic set intersects U in a finite union of translates of subgroups definable in the group structure of U alone. Whence Uind is nothing more than a (divisible) abelian group, which is ω–stable.

This paper looks at the concept of neighborhood canonicity introduced by Brian Chellas [2]. We follow the lead of the author's paper [9] where it was shown that every non-iterative logic is neighborhood canonical and here we will show that all logics whose axioms have a simple syntactic form—no intensional operator is in boolean combination with a propositional letter—and which have the finite model property are neighborhood canonical. One consequence of this is that KMcK, the McKinsey logic, is neighborhood canonical, an interesting counterpoint to the results of Robert Goldblatt and Xiaoping Wang who showed, respectively, that KMcK is not relational canonical [5] and that KMcK is not relationally strongly complete [11].

In examples like the total recursive functions or the computable real numbers the canonical indexings are only partial maps. It is even impossible in these cases to find an equivalent total numbering. We consider effectively given topological T0-spaces and study the problem in which cases the canonical numberings of such spaces can be totalized, i.e., have an equivalent total indexing. Moreover, we show under very natural assumptions that such spaces can effectively and effectively homeomorphically be embedded into a totally indexed algebraic partial order that is closed under the operation of taking least upper bounds of enumerable directed subsets.

Unfoldable cardinals are preserved by fast function forcing and the Laver-like preparations that fast functions support. These iterations show, by set-forcing over any model of ZFC, that any given unfoldable cardinal κ can be made indestructible by the forcing to add any number of Cohen subsets to κ.

We prove that there are uncountably many sets that are low for the class of Schnorr random reals. We give a purely recursion theoretic characterization of these sets and show that they all have Turing degree incomparable to 0′. This contrasts with a result of Kučera and Terwijn [5] on sets that are low for the class of Martin-Löf random reals.

The field K((G)) of generalized power series with coefficients in the field K of characteristic 0 and exponents in the ordered additive abelian group G plays an important role in the study of real closed fields. Conway and Gonshor (see [2, 4]) considered the problem of existence of non-standard irreducible (respectively prime) elements in the huge “ring” of omnific integers, which is indeed equivalent to the existence of irreducible (respectively prime) elements in the ring K((G≤0)) of series with non-positive exponents. Berarducci (see [1]) proved that K((G≤0)) does have irreducible elements, but it remained open whether the irreducibles are prime i.e., generate a prime ideal. In this paper we prove that K((G≤0)) does have prime elements if G = (ℝ, +) is the additive group of the reals, or more generally if G contains a maximal proper convex subgroup.

We prove that the set of properties describable by a uniform sequence of first-order sentences using at most k + 1 distinct variables is exactly equal to the set of properties checkable by a Turing machine in DSPACE[nk] (where n is the size of the universe). This set is also equal to the set of properties describable using an iterative definition for a finite set of relations of arity k. This is a refinement of the theorem PSPACE = VAR[O[1]] [8]. We suggest some directions for exploiting this result to derive trade-offs between the number of variables and the quantifier depth in descriptive complexity.

Introduction. In his monograph On Numbers and Games [7], J. H. Conway introduced a real-closed field containing the reals and the ordinals as well as a great many other numbers including ω, ω, /2, 1/ω, and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered “number” fields—be individually definable in terms of sets of von Neumann-Bernays-Gödel set theory with Global Choice, henceforth NBG [cf. 21, Ch. 4], it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system of real numbers bears to Archimedean ordered fields. This can be made precise by saying that whereas the ordered field of reals is (up to isomorphism) the unique homogeneous universal Archimedean ordered field, No is (up to isomorphism) the unique homogeneous universal orderedfield [14]; also see [10], [12], [13].

However, in addition to its distinguished structure as an ordered field, No has a rich hierarchical structure that (implicitly) emerges from the recursive clauses in terms of which it is defined. This algebraico-tree-theoretic structure, or simplicity hierarchy, as we have called it [15], depends upon No's (implicit) structure as a lexicographically ordered binary tree and arises from the fact that the sums and products of any two members of the tree are the simplest possible elements of the tree consistent with No's structure as an ordered group and an ordered field, respectively, it being understood that x is simpler than y just in case x is a predecessor of y in the tree.

In this paper we show that it is consistent with ZFC that the cardinality of every maximal cofinitary group of Sym(ω) is strictly greater than the cardinal numbers and .

We determine the exact bounds for the length of an arbitrary reduction sequence of a term in the typed λ-calculus with β-, ξ- and η-conversion. There will be two essentially different classifications, one depending on the height and the degree of the term and the other depending on the length and the degree of the term.

We prove a main gap theorem for locally saturated submodels of a homogeneous structure. We also study the number of locally saturated models, which are not elementarily embeddable into each other.

We define a class of productiveσ-ideals of subsets of the Cantor space 2ω and observe that both σ-ideals of meagre sets and of null sets are in this class. From every productive σ-ideal we produce a σ-ideal of subsets of the generalized Cantor space 2κ. In particular, starting from meagre sets and null sets in 2ω we obtain meagre sets and null sets in 2ω, respectively. Then we investigate additivity, covering number, uniformity and cofinality of . For example, we show that

Our results generalizes those from [5].

We present an axiomatic framework for nonstandard analysis—the Nonstandard Class Theory (NCT) which extends von Neumann–Gödel–Bernays Set Theory (NBG) by adding a unary predicate symbol St to the language of NBG (St(X) means that the class X is standard) and axioms—related to it—analogs of Nelson's idealization, standardization and transfer principles. Those principles are formulated as axioms, rather than axiom schemes, so that NCT is finitely axiomatizable. NCT can be considered as a theory of definable classes of Bounded Set Theory by V. Kanovei and M. Reeken. In many aspects NCT resembles the Alternative Set Theory by P. Vopenka. For example there exist semisets (proper subclasses of sets) in NCT and it can be proved that a set has a standard finite cardinality iff it does not contain any proper subsemiset. Semisets can be considered as external classes in NCT. Thus the saturation principle can be formalized in NCT.