Let < and ≼ be two distinguished binary relation symbols. A structure 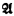is κ-like iff 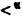is a linear ordering of A, card(A) = κ, and every proper initial segment of A has cardinality < κ. A structure 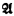is α-ordered iff 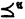is a (reflexive) linear ordering of type α with field a subset of A. We define when a cardinal κ is α-inaccessible. (In this paper, inaccessible always means weakly inaccessible.) The 0-inaccessible cardinals are just the inaccessible cardinals; if α > 0, then κ is α-inaccessible iff for each β < α, each closed, cofinal subset of κ contains a β-inaccessible. (The (1 + α)-inaccessibles are just the ρα cardinals of Mahlo.) This paper is concerned with the proof of the following theorem.

Main Theorem. There is an elementary sentence σ with the property that whenever α is an ordinal and κ an infinite cardinal, then σ has an α-ordered κ-like model iff κ is not α-inaccessible.

This theorem gives some additional answers to a question of Mostowski about languages with generalized quantifiers. Fuhrken [1] showed that this question is equivalent to the following one: For which cardinals κ and λ is it true that if an elementary sentence has a κ-like model, then it has a λ-like model? It is actually this question to which the theorem refers. The theorem limits the possible pairs κ, λ of cardinals which answer the question. In fact, if the question is generalized so as to permit sentences from some more extensive language, then the theorem still limits the possible answers. For a more thorough introduction to this problem, the reader is referred to the aforementioned article of Fuhrken as well as Keisler [2] and Vaught [6].