No CrossRef data available.
Article contents
Theories without countable models
Published online by Cambridge University Press: 12 March 2014
Extract
Consider the Löwenheim-Skolem theorem in the form: If a theory in a countable first-order language has a model, then it has a countable model. As is well known, this theorem becomes false if one omits the hypothesis that the language be countable, for one then has the following trivial counterexample.
Example 1. Let the language have uncountably many constants, and let the theory say that they are unequal.
To motivate some of our future definitions and to introduce some notation, we present another, less trivial, counterexample.
Example 2. Let L0 be the language whose n-place predicate (resp. function) symbols are all the n-place predicates (resp. functions) on the set ω of natural numbers. Let 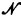 be the standard model for L0; we use the usual notation Th(
be the standard model for L0; we use the usual notation Th(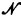 ) for its complete theory. Add to L0 a new constant e, and add to Th(
) for its complete theory. Add to L0 a new constant e, and add to Th(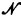 ) an axiom schema saying that e is infinite. By the compactness theorem, the resulting theory T has models. However, none of its models are countable. Although this fact is well known, we sketch a proof in order to refer to it later.
) an axiom schema saying that e is infinite. By the compactness theorem, the resulting theory T has models. However, none of its models are countable. Although this fact is well known, we sketch a proof in order to refer to it later.
By [5, p. 81], there is a family {Aα ∣ < α < c} of 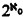 infinite subsets of ω, the intersection of any two of which is finite.
infinite subsets of ω, the intersection of any two of which is finite.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972


