In [2] “recursive frames” were introduced as a means of extending relations R on the nonnegative integers to relations RΛ on the isols. In [1], this extension procedure was generalized by the introduction of “partial recursive frames”; the resulting extended relation on the isols was called RΛ. It was shown in [1] that the two extension procedures agree for recursive relations R, while RΛ ⊇ RΛ if R is 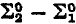. The case when R is 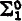, nonrecursive was left open. We show in this note that the extension procedures in fact agree for all 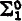relations R.

In the following, the notation and terminology is that of [1] and [2].

Theorem. If R ⊆ XκQ is a recursively enumerable (r.e.) relation, then RΛ = RΛ.

Proof. Clearly RΛ ⊆ RΛ, since every recursive frame is partial recursive. To prove RΛ ⊆ RΛ, we give a uniform effective method for expanding any partial recursiveR-frame F to a recursiveR-frame G such that F ⊆ G, so that 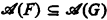So let F be a (nonempty) partial recursive R-frame, with CF(α) generated by 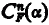. Let Rn denote the result of performing n steps in a fixed recursive enumeration of R. If g(α) is a partial recursive function, “g(α) is defined in n steps” means that in whichever coding of recursive computations is being used, a terminating computation for g with argument α has length ≤ n.