The structures of some laminar boundary layers in high-density, shock heated, 1 eV argon plasma flows have been investigated theoretically. The analysis is based upon a three-fluid continuum formulation. Boundary-layer equations have been solved numerically on a digital computer by a finite difference technique for the case of thermochemical equilibrium and no radiation and applied electromagnetic fields. The induced electric field has been considered and shown to be important. It strongly couples the diffusive motions of the electron and ion fluids, thus forming ambipolar motion except in a sheath region adjacent to the wall. Argon transport properties, calculated from simple kinetic theory, have been used in the analysis. Important parameters, such as the Prandtl number and the density-viscosity product have been found to vary one or two orders of magnitude in the argon plasma boundary layer, a finding in sharp contrast with results for classical, non-ionized boundary layers. Solutions have been developed for the simple Rayleigh's boundary layer (forming over an infinite flat plate with an impulsively started motion in its own plane) and for the shock-tube side-wall boundary layer (forming behind a plane, ionizing shock wave moving over an infinite, plane wall). Even in terms of appropriate similarity parameters, solutions (for e.g. velocity and temperature profiles) exhibit strong dependence upon free- stream conditions. Assumptions of chemical and temperature equilibria have been checked from the equilibrium solution. Results indicate equilibrium ionization would not be present in typical argon boundary layers, e.g. at temperatures below 9000 °K, at a pressure of 1 atm. Similarly, due to ineffective energy transfer rates between the electron and the heavy-particle fluids and the difference in electron and ion–atom thermal conductivities, the electron temperature would deviate from the heavy-particle temperature in the same temperature region. The electron temperature has been calculated in a linearized model and found to be larger than the ion–atom temperature.

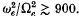 The structure of the dispersion curves for these large values of plasma parameter differs from that for smaller values
The structure of the dispersion curves for these large values of plasma parameter differs from that for smaller values 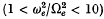 investigated by others, in that broad bands in wave-number space have very small group speeds in narrow frequency bands close to many of the gyrofrequency harmonics. All of the Bernstein modes examined have group speeds less than 37 % of the ion thermal speed, and can be classified as very slow waves. Furthermore, the spectrum of propagating Bernstein modes is broadened as
investigated by others, in that broad bands in wave-number space have very small group speeds in narrow frequency bands close to many of the gyrofrequency harmonics. All of the Bernstein modes examined have group speeds less than 37 % of the ion thermal speed, and can be classified as very slow waves. Furthermore, the spectrum of propagating Bernstein modes is broadened as 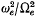 becomes large, with an effective total transmission region from the gyrofrequency up to several harmonics of gyrofrequency
becomes large, with an effective total transmission region from the gyrofrequency up to several harmonics of gyrofrequency