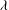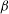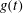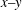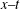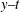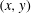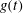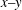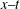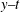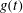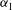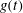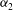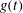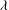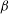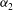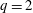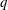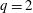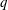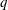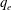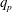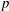A forced and damped Zakharov–Kuznetsov equation for a magnetized electron–positron–ion plasma affected by an external force is studied in this paper. Via the Hirota method, the soliton-like solutions are given. The soliton’s amplitude gets enhanced with the phase velocity 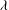 ${\it\lambda}$ decreasing or ion-to-electron density ratio
${\it\lambda}$ decreasing or ion-to-electron density ratio 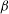 ${\it\beta}$ increasing. With the damped coefficient increasing, when the external force
${\it\beta}$ increasing. With the damped coefficient increasing, when the external force 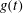 $g(t)$ is periodic, the two solitons are always parallel during the propagation and background of the two solitons drops on the
$g(t)$ is periodic, the two solitons are always parallel during the propagation and background of the two solitons drops on the 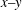 $x{-}y$ plane, and amplitudes of the two solitons increase on the
$x{-}y$ plane, and amplitudes of the two solitons increase on the 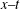 $x{-}t$ and
$x{-}t$ and 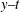 $y{-}t$ planes, with
$y{-}t$ planes, with 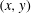 $(x,y)$ as the coordinates of the propagation plane and
$(x,y)$ as the coordinates of the propagation plane and  $t$ as the time. When
$t$ as the time. When 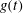 $g(t)$ is exponentially decreasing, the two solitons merge into a single one and the background rises on the
$g(t)$ is exponentially decreasing, the two solitons merge into a single one and the background rises on the 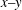 $x{-}y$ plane, and amplitudes of the two solitons decrease on the
$x{-}y$ plane, and amplitudes of the two solitons decrease on the 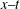 $x{-}t$ and
$x{-}t$ and 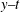 $y{-}t$ planes. Further, associated chaotic motions are obtained when
$y{-}t$ planes. Further, associated chaotic motions are obtained when 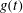 $g(t)$ is periodic. Using the phase projections and Poincaré sections, we find that the chaotic motions can be weakened with
$g(t)$ is periodic. Using the phase projections and Poincaré sections, we find that the chaotic motions can be weakened with 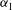 ${\it\alpha}_{1}$ , the amplitude of
${\it\alpha}_{1}$ , the amplitude of 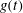 $g(t)$ , decreasing. With
$g(t)$ , decreasing. With 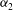 ${\it\alpha}_{2}$ , the frequency of
${\it\alpha}_{2}$ , the frequency of 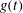 $g(t)$ , decreasing, a three-dimensional attractor with stretching-and-folding structure is found, indicating that the weak chaos is transformed into the developed chaos. Chaotic motions can also be weakened with
$g(t)$ , decreasing, a three-dimensional attractor with stretching-and-folding structure is found, indicating that the weak chaos is transformed into the developed chaos. Chaotic motions can also be weakened with 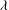 ${\it\lambda}$ , the phase velocity, decreasing, but strengthened with
${\it\lambda}$ , the phase velocity, decreasing, but strengthened with 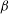 ${\it\beta}$ , the ion-to-electron density ratio, and
${\it\beta}$ , the ion-to-electron density ratio, and 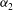 ${\it\alpha}_{2}$ decreasing.
${\it\alpha}_{2}$ decreasing.
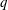 $q$ -nonextensive electrons and positrons
$q$ -nonextensive electrons and positrons