Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T11:09:58.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of parallel sound wave damping and drift kinetic damping on the resistive wall mode stability with various plasma rotation profiles

Published online by Cambridge University Press:  18 August 2015

Chao Liu  and
Yue Liu
Chao Liu
Affiliation:
Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams (Ministry of Education), School of Physics and Optoelectronic Technology, Dalian University of Technology, Dalian 116024, China
Yue Liu*
Affiliation:
Key Laboratory of Materials Modification by Laser, Ion, and Electron Beams (Ministry of Education), School of Physics and Optoelectronic Technology, Dalian University of Technology, Dalian 116024, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of a parallel viscous force induced damping and the magnetic precessional drift resonance induced damping on the stability of the resistive wall mode (RWM) is numerically investigated for one of the advanced steady-state scenarios in international thermonuclear experimental reactor (ITER). The key element of the investigation is to study how different plasma rotation profiles affect the stability prediction. The single-fluid, toroidal magnetohydrodynamic (MHD) code MARS-F (Liu et al., Phys. Plasmas, vol. 7, 2000, p. 3681) and the MHD–kinetic hybrid code MARS-K (Liu et al., Phys. Plasmas, vol. 15, 2008, 112503) are used for this purpose. Three extreme rotation profiles are considered: (a) a uniform profile with no shear, (b) a profile with negative flow shear at the 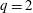$q=2$ rational surface ( 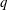$q$ is the equilibrium safety factor), and (c) a profile with positive shear at 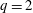$q=2$ . The parallel viscous force is found to be effective for the mode stabilization at high plasma flow speed (about a few percent of the Alfven speed) for the no shear flow profile and the negative shear flow profile, but the stable domain does not appear with the positive shear flow profile. The predicted eigenmode structure is different with different rotation profiles. With a self-consistent inclusion of the magnetic precession drift resonance of thermal particles in MARS-K computations, a lower critical flow speed, i.e. the minimum speed needed for full suppression of the mode, is obtained. Likewise the eigenmode structure is also modified by different rotation profiles in the kinetic results.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 905810516
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aymar, R., Barabaschi, P. & Shimomura, Y. 2002 The ITER design. Plasma Phys. Control. Fusion 44, 519–565.Google Scholar
Berkery, J. W., Liu, Y. Q., Wang, Z. R., Sabbagh, S. A., Logan, N. C., Park, J.-K., Manickam, J. & Betti, R. 2014 Benchmarking kinetic calculations of resistive wall mode stability. Phys. Plasmas 21, 052505.Google Scholar
Bierwage, A., Yu, Q. Q. & Günter, S. 2007 Large-mode-number magnetohydrodynamic instability driven by sheared flows in a tokamak plasma with reversed central shear. Phys. Plasmas 14, 010704.Google Scholar
Bondeson, A., Liu, Y. Q., Fransson, C. M., Lennartson, B., Breitholtz, C. & Taylor, T. S. 2001 Active feedback stabilization of high beta modes in advanced tokamaks. Nucl. Fusion 41, 455–463.Google Scholar
Bondeson, A. & Xie, H. X. 1997 Stability of ideal and resistive modes in cylindrical plasmas with resistive walls and plasma rotation. Phys. Plasmas 4, 2081–2089.Google Scholar
Chapman, I. T., Brown, S., Kemp, R. & Walkden, N. R. 2012 Toroidal velocity shear Kelvin–Helmholtz instabilities in strongly rotation tokamak plasmas. Nucl. Fusion 52, 042005.Google Scholar
Chapman, I. T., Gimblett, C. G., Gryaznevich, M. P., Hender, T. C., Howell, D. F., Liu, Y. Q., Pinches, S. D.& JET EFDA Contributors 2009 Stability of the resistive wall mode in JET. Plasma Phys. Control. Fusion 51, 055015.Google Scholar
Chapman, I. T., Liu, Y. Q., Asunta, O., Graves, J. P., Johnson, T. & Jucker, M. 2012 Kinetic damping of resistive wall modes in ITER. Phys. Plasmas 19, 052502.Google Scholar
Chapman, I. T., Walkden, N. R., Graves, J. P. & Wahlberg, C. 2011 The effects of shered toroidal rotation on stability limits in tokamak plasmas. Plasma Phys. Control. Fusion 53, 125002.Google Scholar
Chu, M. S. 1998 Shear flow destabilization of a slowly rotating tokamak. Phys. Plasmas 5, 183–191.Google Scholar
Chu, M. S., Greene, J. M., Jensen, T. H., Miller, R. L., Bondeson, A., Johnson, R. W. & Mauel, M. E. 1995 Effect of toroidal plasma flow and flow shear on global magnetohydrodynamic MHD modes. Phys. Plasmas 2, 2236–2241.Google Scholar
Chu, M. S. & Okabayashi, M. 2010 Stabilization of the external kink and the resistive wall mode. Plasma Phys. Control. Fusion 52, 123001.CrossRefGoogle Scholar
Drake, J. R., Brunsell, P. R., Yadikin, D., Cecconello, M., Malmberg, J. A., Gregoratto, D., Paccagnella, R., Bolzonella, T., Manduchi, G., Marrelli, L., Ortolani, S., Spizzo, G., Zanca, P., Bondeson, A. & Liu, Y. Q. 2005 Experimental and theoretical studies of active control of resistive wall mode growth in the EXTRAP T2R reversed-field pinch. Nucl. Fusion 45, 557–564.Google Scholar
Fransson, C. M., Lennartson, B., Breitholtz, C., Bondeson, A. & Liu, Y. Q. 2000 Feedback stabilization of nonaxisymmetric resistive wall modes in tokamaks. II. Control analysis. Phys. Plasmas 7, 4143–4151.Google Scholar
Gregoratto, D., Drake, J. R., Yadikin, D., Liu, Y. Q., Paccagnella, R., Brunsell, P. R., Bolzonella, T., Marchiori, G. & Cecconello, M. 2005 Studies on the response of resisitve-wall modes to applied magnetic perturbations in the EXTRAP T2R reversed field pinch. Phys. Plasmas 12, 092510.Google Scholar
Hao, G. Z., Liu, Y. Q., Wang, A. K. & Qiu, X. M. 2012 Kinetic effects of trapped energetic particles on stability of external kink modes with a resistive wall. Phys. Plasmas 19, 032507.Google Scholar
Hao, G. Z., Wang, A. K., Liu, Y. Q. & Qiu, X. M. 2011 Effect of trapped energetic particles on the resistive wall mode. Phys. Rev. Lett. 107, 015001.Google Scholar
He, Y. L., Liu, Y. Q., Liu, Y., Hao, G. Z. & Wang, A. 2014 Plasma-resistivity-induced strong damping of the kinetic resistive wall mode. Phys. Rev. Lett. 113, 175001.Google Scholar
Hu, B. & Betti, R. 2004 Resistive wall mode in collision-less quasistationary plasmas. Phys. Rev. Lett. 93, 105002.CrossRefGoogle Scholar
Kessel, C., Manickam, J., Rewoldt, G. & Tang, W. M. 1994 Improved plasma performance in tokamaks with negative magnetic shear. Phys. Rev. Lett. 72, 1212–1215.Google Scholar
Liu, Y. Q. 2010 Effect of ${\it\alpha}$ particles on the resistive wall mode stability in ITER. Nucl. Fusion 50, 095008.Google Scholar
Liu, Y. Q. & Bondeson, A. 2000 Active feedback stabilization of toroidal external modes in tokamaks. Phys. Rev. Lett. 84, 907–910.CrossRefGoogle ScholarPubMed
Liu, Y. Q., Bondeson, A., Chu, M. S., Favez, J.-Y., Gribov, Y., Gryaznevich, M., Hender, T. C., Howell, D. F., LaHaye, R. J., Lister, J. B., de Vries, P.& EFDA JET Contributors 2005a Feedback and rotational stabilization of resistive wall modes in ITER. Nucl. Fusion 45, 1131–1139.Google Scholar
Liu, Y. Q., Bondeson, A., Fransson, C. M., Lennartson, B. & Breitholtz, C. 2000 Feedback stabilization of nonaxisymmetric resistive wall modes in tokamaks. I. Electromagnetic model. Phys. Plasmas 7, 3681–3690.CrossRefGoogle Scholar
Liu, Y. Q., Bondeson, A., Gribov, Y. & Polevoi, A. 2004 Stabilization of resisitive wall modes in ITER by active feedback and toroidal rotation. Nucl. Fusion 44, 232–242.Google Scholar
Liu, Y. Q., Chapman, I. T., Chu, M. S., Reimerdes, H., Villone, F., Albanese, R., Ambrosino, G., Garofalo, A. M., Gimblett, C. G., Hastie, R. J., Hender, T. C., Jackson, G. L., La Haye, R. J., Okabayashi, M., Pironti, A., Portone, A., Rubinacci, G. & Strait, E. J. 2009 Progress in physics and control of the resistive wall mode in advanced tokamaks. Phys. Plasmas 16, 056113.Google Scholar
Liu, Y. Q., Chu, M. S., Chapman, I. T. & Hender, T. C. 2008 Toroidal self-consistent modeling of drift kinetic effects on the resistive wall mode. Phys. Plasmas 15, 112503.Google Scholar
Liu, Y. Q., Chu, M. S., Chapman, I. T. & Hender, T. C. 2009 Modelling resistive wall modes in ITER with self-consistent inclusion of drift kinetic resonances. Nucl. Fusion 49, 035004.CrossRefGoogle Scholar
Liu, Y. Q., Chu, M. S., Garofalo, A. M., LaHaye, R. J., Gribov, Y., Gryaznevich, M., Hender, T. C., Howell, D. F., de Vries, P., Okabayashi, M., Pinches, S. D., Reimerdes, H.& EFDA JET Contributors 2005b Modeling of resistive wall mode and its control in experiments and ITER. Phys. Plasmas 13, 056120.Google Scholar
Liu, Y. Q., Chu, M. S., Gimblett, C. G. & Hastie, R. J. 2008 Magnetic drift kinetic damping of the resisitve wall mode in large aspect ratio tokamaks. Phys. Plasmas 15, 092505.Google Scholar
Liu, Y. Q., Chu, M. S., Guo, W. F., Villone, F., Albanese, R., Ambrosino, G., Baruzzo, M., Bolzonella, T., Chapman, I. T., Garofalo, A. M., Gimblett, C. G., Hastie, R. J., Hender, T. C., Jackson, G. L., La Haye, R. J., Lanctot, M. J., In, Y., Marchiori, G., Okabayashi, M., Paccagnella, R., Furno Palumbo, M., Pironti, A., Reimerdes, H., Rubinacci, G., Soppelsa, A., Strait, E. J., Ventre, S. & Yadykin, D. 2010 Resistive wall mode control code maturity: progress and specific examples. Plasma Phys. Control. Fusion 52, 104002.Google Scholar
Martin, P., Apolloni, L., Puiatti, M. E., Adamek, J., Agostini, M., Alfier, A., Annibaldi, S. V., Antoni, V., Auriemma, F., Barana, O., Baruzzo, M., Bettini, P., Bolzonella, T., Bonfiglio, D., Bonomo, F., Brombin, M., Brotankova, J., Buffa, A., Buratti, P., Canton, A., Cappello, S., Carraro, L., Cavazzana, R., Cavinato, M., Chapman, B. E., Chitarin, G., Dal Bello, S., De Lorenzi, A., De Masi, G., Escande, D. F., Fassina, A., Ferro, A., Franz, P., Galo, E., Gazza, E., Giudicotti, L., Gnesotto, F., Gobbin, M., Grando, L., Guazzotto, L., Guo, S. C., Igochine, V., Innocente, P., Liu, Y. Q., Lorenzini, R., Luchetta, A., Manduch, G., Marchiori, G., Marcuzzi, D., Marrelli, L., Martini, S., Martines, E., McCollam, K., Menmuir, S., Milani, F., Moresco, M., Novello, L., Ortolani, S., Paccagnella, R., Pasqualotto, R., Peruzzo, S., Piovan, R., Piovesan, P., Piron, L., Pizzimenti, A., Pomaro, N., Predebon, I., Reusch, J. A., Rostagni, G., Rubinacci, G., Sarft, J. S., Sattin, F., Scarin, P., Serianni, G., Sonato, P., Spada, E., Soppelsa, A., Spagnolo, S., Spolaore, M., Spizzo, G., Taliercio, C., Terranova, D., Toigo, V., Valisa, M., Vianello, N., Villone, F., White, R. B., Yadikin, D., Zaccaria, P., Zamengo, A., Zanca, P., Zaniol, B., Zanotto, L., Zilli, E., Zohm, H. & Zuin, M. 2009 Overview of RFX-mod results. Nucl. Fusion 49, 104019.Google Scholar
Reimerdes, H., Garofalo, A. M., Jackson, G. L., Okabayashi, M., Strait, E. J., Chu, M. S., In, Y., La Haye, R. J., Lanctot, M. J., Liu, Y. Q., Navratil, G. A., Solomon, W. M., Takahashi, H. & Groebner, R. J. 2007 Reduced critical rotation for resistive-wall mode stabilization in a near-axisymmetric configuration. Phys. Rev. Lett. 98, 055001.Google Scholar
Reimerdes, H., Hender, T. C., Sabbagh, S. A., Bialek, J. M., Chu, M. S., Garofalo, A. M., Gryaznevich, M. P., Howell, D. F., Jackson, G. L., La Haye, R. J., Liu, Y. Q., Menard, J. R., Navratil, G. A., Okabayashi, M., Pinches, S. D., Sontag, A. C., Strait, E. J., Zhu, W., Bigi, M., de Baar, M., de Vries, P., Gates, D. A., Gohil, P., Groebner, R. J., Mueller, D., Raman, R., Scoville, J. T., Solomon, W. M.& the DIII-D Team, JET-EFDA Contributors and the NSTX Team 2006 Cross-machine comparison of resonant field amplification and resistive wall mode stabilization by plasma rotation. Phys. Plasmas 13, 056107.CrossRefGoogle Scholar
Takechi, M., Matsunaga, G., Aiba, N., Fujita, T., Ozeki, T., Koide, Y., Sakamoto, Y., Kurita, G., Isayama, A., Kamada, Y.& the JT-60 team 2007 Identification of a low plasma-rotation threshold for stabilization of the resistive-wall mode. Phys. Rev. Lett. 98, 055002.Google Scholar
Troyon, F., Gruber, R., Saurenmann, H., Semenzato, S. & Succi, S. 1984 MHD-limits to plasma confinement. Plasma Phys. Control. Fusion 26, 209.Google Scholar
Villone, F., Liu, Y. Q., Rubinacci, G. & Ventre, S. 2010 Effects of thick blanket modules on the resistive wall modes stability in ITER. Nucl. Fusion 50, 125001.Google Scholar
Wahlberg, C., Graves, J. P. & Chapman, I. T. 2013 Analysis of global hydromagnetic instabilities driven by strongly sheared toroidal flows in tokamak plasmas. Plasma Phys. Control. Fusion 55, 105004.Google Scholar
Wang, Z. R., Guo, S. C. & Liu, Y. Q. 2012 Drift kinetic effects on the resistive wall mode stability-comparison between reversed field pinches and tokamaks. Phys. Plasmas 19, 072518.Google Scholar
Wang, Z. R., Lanctot, M. J., Liu, Y. Q., Park, J.-K. & Menard, J. E. 2015 Three-dimensional drift kinetic response of high- ${\it\beta}$ plasma in the DIII-D tokamak. Phys. Rev. Lett. 114, 145005.Google Scholar
Ward, D. J. & Bondeson, A. 1995 Stabilization of ideal modes by resistive walls in tokamaks with plasma rotation and its effect on the beta limit. Phys. Plasmas 2, 1570–1580.Google Scholar
Zheng, L. J., Kotschenreuther, M. T. & Van Dam, J. W. 2009 Kinetic analysis of the resistive wall modes in the ITER advanced tokamak scenario. Nucl. Fusion 49, 075021.Google Scholar