No CrossRef data available.
Published online by Cambridge University Press: 12 February 2024
Radio frequency quadrupole coolers (RFQCs) are very suitable to cool ion beams with moderate energy spread, typically ions of exotic nuclear species (like $^{132}$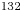 Sn$^{1+}$
Sn$^{1+}$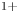 ) as in the Selective Production of Exotic Species project at the Laboratori Nazionali di Legnaro, whose ion source supplies 40 keV ions. Beam dynamics includes ion–gas collisions (with a balance of cooling and diffusion effects), acceleration and deceleration and radiofrequency confinement, which can be supplemented by static magnetic field effects. Insertion of a prototype RFQC in the solenoid of the Eltrap machine is also discussed here, with innovations in beam extraction and in modelling, now also based on stochastic equations. Practical consideration on gas pumping and voltage distribution are also included. Typical limits of RFQC are discussed, with special attention to the extracted beam root mean square emittance, which is shown to strongly depend not only on cooler parameters, but also on extraction optics.
) as in the Selective Production of Exotic Species project at the Laboratori Nazionali di Legnaro, whose ion source supplies 40 keV ions. Beam dynamics includes ion–gas collisions (with a balance of cooling and diffusion effects), acceleration and deceleration and radiofrequency confinement, which can be supplemented by static magnetic field effects. Insertion of a prototype RFQC in the solenoid of the Eltrap machine is also discussed here, with innovations in beam extraction and in modelling, now also based on stochastic equations. Practical consideration on gas pumping and voltage distribution are also included. Typical limits of RFQC are discussed, with special attention to the extracted beam root mean square emittance, which is shown to strongly depend not only on cooler parameters, but also on extraction optics.