The stability of axisymmetric vortices to inertial perturbations is investigated by means of linear stability analysis, taking into account stratification, vertical eddy viscosity, as well as finite depth of the flow. We consider different types of circular barotropic vortices in a linearly stratified shallow layer confined with rigid lids. For the simplest case of the Rankine vortex we develop an asymptotic analytic dispersion relation and a marginal stability criterion, which compares well with numerical results. This is a further generalization to the well-known generalized Rayleigh criterion, which is only valid for non-dissipative and non-stratified eddies. Unlike the Rayleigh criterion, it predicts that intense anticyclones may be stable even with a core region of negative absolute vorticity, and that the dissipation and stratification work together to stabilize the flow. Numerical analysis reveals that the stability diagrams for various types of vortices are almost identical in the Rossby, Burger and Ekman parameter space. This allows extension of our analytical solutions for the Rankine vortex to a wide variety of vortices. Furthermore, we show that a more suitable parameter for the intensity of the vortex is the vortex Rossby number, while for the inviscid case it is the local normalized vorticity. These predictions are in agreement with laboratory experiments presented in part 2 (J. Fluid Mech., vol. 732, 2013, pp. 485–509).

Large-scale laboratory experiments were performed on the Coriolis rotating platform to study the stability of intense vortices in a thin stratified layer. A linear salt stratification was set in the upper layer on top of a thick barotropic layer, and a cylinder was towed in the upper layer to produce shallow cyclones and anticyclones of similar size and intensity. We focus our investigations on submesoscale eddies, where the radius is smaller than the baroclinic deformation radius. Towing speed, cylinder size and stratification were changed in order to cover a large range of the parameter space, staying in a relatively high horizontal Reynolds number ($Re= 2000{{\unicode{x2013}}}7000$). The Rayleigh criterion states that inertial instabilities should strongly destabilize intense anticyclonic eddies if the vorticity in the vortex core is negative enough ${\zeta }_{0} / f\lt - 1$, where ${\zeta }_{0} $ is the relative vorticity in the core of the vortex, and $f$ is the Coriolis parameter. However, we found that some anticyclones remain stable even for very intense negative vorticity values, up to ${\zeta }_{0} / f= - 3. 5$, when the Burger number is large enough. This is in agreement with the linear stability analysis performed in part 1 (J. Fluid Mech., vol. 732, 2013, pp. 457–484), which shows that the combined effect of a strong stratification and a moderate vertical dissipation may stabilize even very intense anticyclones, and the unstable eddies we found were located close to the marginal stability limit. Hence, these experimental results agree well with the simple stability diagram proposed in the Rossby, Burger and Ekman parameter space for inertial destabilization of viscous anticyclones within a shallow and stratified layer.

It is generally accepted that the effective velocity of a viscous flow over a porous bed satisfies the Beavers–Joseph slip law. To the contrary, the interface law for the effective stress has been a subject of controversy. Recently, a pressure jump interface law has been rigourously derived by Marciniak-Czochra and Mikelić. In this paper, we provide a confirmation of the analytical result using direct numerical simulation of the flow at the microscopic level. To the best of the authors’ knowledge, this is the first numerical confirmation of the pressure interface law in the literature.

We consider the propagation of a high-Reynolds-number gravity current in a horizontal channel along the horizontal coordinate $x$. The bottom and top of the channel are at 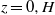$z= 0, H$, and the cross-section is given by the quite general 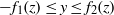$- {f}_{1} (z)\leq y\leq {f}_{2} (z)$ for 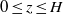$0\leq z\leq H$. We develop a two-layer shallow-water (SW) formulation, and we implement it for the solution of the dam-break problem. The dependent variables are the position of the interface, 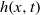$h(x, t)$, and the velocity (averaged over the area of the current), 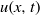$u(x, t)$. The non-rectangular cross-section geometry enters the formulation via 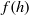$f(h)$ and integrals of 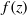$f(z)$ and 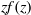$zf(z)$, where 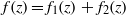$f(z)= {f}_{1} (z)+ {f}_{2} (z)$ is the width of the channel. For a given geometry 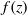$f(z)$, the free input parameters of the lock-release problem are: (i) the height ratio 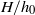$H/ {h}_{0} $ of ambient to lock; and (ii) the density ratio of ‘light’ to ‘heavy’ fluids, 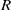$R$. We show that the dam-break problem is amenable to solution by the method of characteristics, but various complications (internal jumps, critical restrictions) appear when the return flow in the ambient is significant; these features are not captured by a one-layer shallow-water model. The role of the non-standard geometry in the detection and calculation of the internal and reflected jumps, and on the dam-break flow field, is elucidated. The methodology is illustrated for Boussinesq flow in typical geometries: power-law (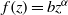$f(z)= b{z}^{\alpha } $, where 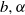$b, \alpha $ are positive constants), trapezoidal and circle (full or sector); we solved for full-depth (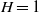$H= 1$) and part-depth (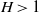$H\gt 1$) lock-release configurations. The approach seems to work well: in all the tested cases, the solution was obtained with simple mathematical and numerical tools (a Runge–Kutta integrator and a secant-method solver); the insights are compatible with our previous understanding of the problem; and the standard (rectangular) case is recovered in the appropriate limit (i.e. when the side-boundaries of the trapezium cross-section are vertical or far apart). A comparison of the speed of propagation with available experiments is also presented, and the agreement is satisfactory. The present solution is a significant generalization of the classical two-layer gravity–current dam-break problem. The classical formulation for a rectangular (or laterally unbounded) channel is now just a particular case, 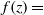$f(z)= $ const., in the wide domain of cross-sections covered by the new model.

Weakly nonlinear interactions involving amplitude-modulated Tollmien–Schlichting waves in an incompressible, two-dimensional aerofoil boundary layer are investigated experimentally. Selected resonant regimes are examined with emphasis on the regimes where more than one fundamental Tollmien–Schlichting (TS) wave is present in the flow. The experiments were performed on an NLF-type aerofoil section for glider applications. Disturbances with controlled frequency-spanwise-wavenumber spectra were excited in the boundary layer and studied by phase-locked hot-wire measurements. The results show that nonlinear mechanisms connected with the steepening of the primary TS wave modulation do not play any significant role in the transition scenarios studied. It is also shown that modulations of the two-dimensional fundamental waves tend to generate additional modes at modulation frequency. These low-frequency disturbances are found to be produced by a non-resonant quadratic combination of spectral components of the primary, modulated TS wave. The investigations show that the efficiency of the process is higher for three-dimensional low-frequency modes in comparison with two-dimensional modes. Thus, the emergence of three-dimensionality for the low-frequency waves does not require any resonant interactions. In a subsequent nonlinear stage, the self-generated detuned subharmonics are found to be strongly amplified due to resonant interactions with the primary TS waves. The sequence of weakly nonlinear mechanisms found and investigated here seems to be the most likely route to the laminar–turbulent transition, at least for two-dimensional boundary layers of aerofoils with a long extent of laminar flow and in a ‘natural’ disturbance environment.

Small-amplitude perturbations are governed by the linearized Navier–Stokes equations, which are, for a parallel or nearly parallel shear flow, customarily reduced to the Orr–Sommerfeld (O-S) and Squire equations. In this paper, we consider continuous spectra (CS) of the O-S and Squire operators for the Blasius and asymptotic suction boundary layers, and address the issue of whether and when continuous modes can represent free-stream vortical disturbances and their entrainment into the shear layer. For the Blasius boundary layer, we highlight two particular properties of the CS: (i) the eigenfunction of a continuous mode simultaneously consists of two components with wall-normal wavenumbers $\pm {k}_{2} $, a phenomenon which we refer to as ‘entanglement of Fourier components’; and (ii) for low-frequency disturbances the presence of the boundary layer forces the streamwise velocity in the free stream to take a much larger amplitude than those of the transverse velocities. Both features appear to be non-physical, and cast some doubt about the appropriateness of using CS to characterize free-stream vortical disturbances and their entrainment into the boundary layer, a practice that has been adopted in some recent studies of bypass transition. A high-Reynolds-number asymptotic description of continuous modes and entrainment is present, and it shows that the entanglement is a result of neglecting non-parallelism, which has a leading-order effect on the entrainment. When this effect is included, entanglement disappears, and moreover the streamwise velocity is significantly amplified in the edge layer when ${R}^{- 1} \ll \omega \ll 1$, where $R$ is the Reynolds number based on the local boundary-layer thickness. For the asymptotic suction boundary layer, which is an exactly parallel flow, both temporal and spatial CS may be defined mathematically. However, at a finite $R$ neither of them represents the physical process of free-stream vortical disturbances penetrating into the boundary layer. The latter must instead be characterized by a peculiar type of continuous modes whose eigenfunctions increase exponentially with the distance from the wall. In the limit $R\gg 1$, all three types of CS are identical at leading order, and hence can be used to represent free-stream vortical disturbances and their entrainment. Low-frequency disturbances are found to generate a large-amplitude streamwise velocity in the boundary layer, which is reminiscent of longitudinal streaks.

In the low-Froude-number limit, free-surface gravity waves caused by flow past a submerged obstacle have amplitude that is exponentially small. Consequently, these cannot be represented using an asymptotic series expansion. Steady linearized flow past a submerged source is considered, and exponential asymptotic methods are applied to determine the behaviour of the free-surface gravity waves. The free surface is found to contain longitudinal and transverse waves that switch on rapidly across curves known as Stokes lines on the free surface. The longitudinal waves are present everywhere downstream of the singularity, while the transverse waves are restricted to two downstream wedges. As the depth of the source approaches the surface, the familiar Kelvin-wedge wave behaviour is recovered.

We consider convection–diffusion transport of a passive scalar within porous media having a piecewise-smooth and reflecting pore–grain interface. The corresponding short-time expansion of molecular displacement time-correlation functions is determined for the generalized steady convection field. By interpreting the generalized short-time expansion of dispersion dynamics in the context of low-Reynolds-number flow through macroscopically homogeneous porous media, we demonstrate the connection between hydrodynamic permeability and short-time dynamics. The analytical short-time expansion is compared with numerical simulation data for steady low-Reynolds-number flow through a random close-pack array of mono-disperse spheres. The quadratic short-time expansion term of the dispersion coefficient closely predicts the numerical data for a mean displacement of at least 10 % of the sphere diameter for a Péclet number of 54.49.

Turbophoresis occurs in wall-bounded turbulent flows where it induces a preferential accumulation of inertial particles towards the wall and is related to the spatial gradients of the turbulent velocity fluctuations. In this work, we address the effects of drag-reducing polymer additives on turbophoresis in a channel flow. The analysis is based on data from a direct numerical simulation of the turbulent flow of a viscoelastic fluid modelled with the FENE-P closure and laden with particles of different inertia. We show that polymer additives decrease the particle preferential wall accumulation and demonstrate with an analytical model that the turbophoretic drift is reduced because the wall-normal variation of the wall-normal fluid velocity fluctuations decreases. As this is a typical feature of drag reduction in turbulent flows, an attenuation of turbophoresis and a corresponding increase in the particle streamwise flux are expected to be observed in all of these flows, e.g. fibre or bubble suspensions and magnetohydrodynamics.

The non-stationary transition from Mach to regular reflection followed by a reverse transition from regular to Mach reflection is investigated experimentally. A new experimental setup in which an incident shock wave reflects from a cylindrical concave surface followed by a cylindrical convex surface of the same radius is introduced. Unlike other studies that indicate problems in identifying the triple point, an in-house image processing program, which enables automatic detection of the triple point, is developed and presented. The experiments are performed in air having a specific heats ratio 1.4 at three different incident-shock-wave Mach numbers: 1.2, 1.3 and 1.4. The data are extracted from high-resolution schlieren images obtained by means of a fully automatically operated shock-tube system. Each experiment produces a single image. However, the high accuracy and repeatability of the control system together with the fast opening valve enables us to monitor the dynamic evolution of the shock reflections. Consequently, high-resolution results both in space and time are obtained. The credibility of the present analysis is demonstrated by comparing the first transition from Mach to regular reflection ($\mathrm{MR} \rightarrow \mathrm{RR} $) with previous single cylindrical concave surface experiments. It is found that the second transition, back to Mach reflection ($\mathrm{RR} \rightarrow \mathrm{MR} $), occurs earlier than one would expect when the shock reflects from a single cylindrical convex surface. Furthermore, the hysteresis is observed at incident-shock-wave Mach numbers smaller than those at which the dual-solution domain starts, which is the minimal value for obtaining hysteresis in steady and pseudo-steady flows. The existence of a non-stationary hysteresis phenomenon, which is different from the steady-state hysteresis phenomenon, is discovered.

Ordinary two-dimensional turbulence corresponds to a Hamiltonian dynamics that conserves energy and the vorticity on fluid particles. This paper considers coupled systems of two-dimensional turbulence with three distinct governing dynamics. One is a Hamiltonian dynamics that conserves the vorticity on fluid particles and a quantity analogous to the energy that causes the system members to develop a strong correlation in velocity. The other two dynamics considered are non-Hamiltonian. One conserves the vorticity on particles but has no conservation law analogous to energy conservation; the other conserves energy and enstrophy but it does not conserve the vorticity on fluid particles. The coupled Hamiltonian system behaves like two-dimensional turbulence, even to the extent of forming isolated coherent vortices. The other two dynamics behave very differently, but the behaviours of all four dynamics are accurately predicted by the methods of equilibrium statistical mechanics.

A recently proposed stabilization mechanism for the Rayleigh–Taylor instability, using magnetic fluids and azimuthally rotating magnetic fields, is experimentally investigated in a cylindrical geometry and compared with the theoretical model. This approach allows the imperfection of the experimental setup to be exploited for measuring the critical field strength of the instability without ever reaching the supercritical state. Furthermore, we use a fast increase in the magnetic field strength to prevent an already occurring instability and force the system back to its initial state. In this way we measure the growth dynamics repeatedly and acquire the characteristic time scale ${\tau }_{0} $ of the instability.