Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T05:11:50.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Unravelling the Rayleigh–Taylor instability by stabilization

Published online by Cambridge University Press:  12 September 2013

A. Poehlmann ,
R. Richter  and
I. Rehberg
A. Poehlmann
Affiliation:
Experimentalphysik V, Universität Bayreuth, D-95440 Bayreuth, Germany
R. Richter*
Affiliation:
Experimentalphysik V, Universität Bayreuth, D-95440 Bayreuth, Germany
I. Rehberg
Affiliation:
Experimentalphysik V, Universität Bayreuth, D-95440 Bayreuth, Germany
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A recently proposed stabilization mechanism for the Rayleigh–Taylor instability, using magnetic fluids and azimuthally rotating magnetic fields, is experimentally investigated in a cylindrical geometry and compared with the theoretical model. This approach allows the imperfection of the experimental setup to be exploited for measuring the critical field strength of the instability without ever reaching the supercritical state. Furthermore, we use a fast increase in the magnetic field strength to prevent an already occurring instability and force the system back to its initial state. In this way we measure the growth dynamics repeatedly and acquire the characteristic time scale 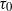${\tau }_{0} $ of the instability.

JFM classification

Complex Fluids: Colloids Flow Control: Flow Control Flow Control: Instability control
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , R3
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
©2013 Cambridge University Press.

References

Evans, R., Bennett, A. & Pert, G. 1982 Rayleigh–Taylor instabilities in laser-accelerated targets. Phys. Rev. Lett. 49 (22), 1639–1642.Google Scholar
Friedrich, T., Lang, T., Rehberg, I. & Richter, R. 2012 Spherical sample holders to improve the susceptibility measurement of superparamagnetic materials. Rev. Sci. Instrum. 83 (4), 045106–045106.CrossRefGoogle ScholarPubMed
Gollwitzer, Ch., Matthis, G., Richter, R., Rehberg, I. & Tobiska, L. 2007 The surface topography of the Rosensweig instability – a quantitative comparison between experiment and numerical simulation. J. Fluid Mech. 571, 455–474.Google Scholar
Ivanov, A. O. & Kuznetsova, O. B. 2001 Magnetic properties of dense ferrofluids: an influence of interparticle correlations. Phys. Rev. E 64 (4), 041405.CrossRefGoogle ScholarPubMed
Lewis, D. J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A 202, 81–96.Google Scholar
Rannacher, D. & Engel, A. 2007 Suppressing the Rayleigh–Taylor instability with a rotating magnetic field. Phys. Rev. E 75 (1), 016311.Google Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Richter, R. & Bläsing, J. 2001 Measuring surface deformations in magnetic fluid by radioscopy. Rev. Sci. Instrum. 72, 1729–1733.Google Scholar
Rosensweig, R. E. 1985 Ferrohydrodynamics. Cambridge University Press.Google Scholar
Smarr, L., Wilson, J., Barton, R. & Bowers, R. 1981 Rayleigh–Taylor overturn in super-nova core collapse. Astrophys. J. 246 (2), 515–525.Google Scholar
Taylor, Sir G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Völtz, C., Pesch, W. & Rehberg, I. 2001 Rayleigh–Taylor instability in a sedimenting suspension. Phys. Rev. E 65, 011404.Google Scholar
Wolf, G. 1969 Dynamic stabilization of Rayleigh–Taylor instability and corresponding dynamic equilibrium. Z. Phys. 227 (3), 291–300.CrossRefGoogle Scholar
Zuidema, H. & Waters, G. 1941 Ring method for determination of interfacial tension. Ind. Engng Chem. Anal. Edn 13 (5), 312–313.Google Scholar