Published online by Cambridge University Press: 02 September 2013
The non-stationary transition from Mach to regular reflection followed by a reverse transition from regular to Mach reflection is investigated experimentally. A new experimental setup in which an incident shock wave reflects from a cylindrical concave surface followed by a cylindrical convex surface of the same radius is introduced. Unlike other studies that indicate problems in identifying the triple point, an in-house image processing program, which enables automatic detection of the triple point, is developed and presented. The experiments are performed in air having a specific heats ratio 1.4 at three different incident-shock-wave Mach numbers: 1.2, 1.3 and 1.4. The data are extracted from high-resolution schlieren images obtained by means of a fully automatically operated shock-tube system. Each experiment produces a single image. However, the high accuracy and repeatability of the control system together with the fast opening valve enables us to monitor the dynamic evolution of the shock reflections. Consequently, high-resolution results both in space and time are obtained. The credibility of the present analysis is demonstrated by comparing the first transition from Mach to regular reflection (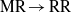 $\mathrm{MR} \rightarrow \mathrm{RR} $) with previous single cylindrical concave surface experiments. It is found that the second transition, back to Mach reflection (
$\mathrm{MR} \rightarrow \mathrm{RR} $) with previous single cylindrical concave surface experiments. It is found that the second transition, back to Mach reflection (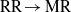 $\mathrm{RR} \rightarrow \mathrm{MR} $), occurs earlier than one would expect when the shock reflects from a single cylindrical convex surface. Furthermore, the hysteresis is observed at incident-shock-wave Mach numbers smaller than those at which the dual-solution domain starts, which is the minimal value for obtaining hysteresis in steady and pseudo-steady flows. The existence of a non-stationary hysteresis phenomenon, which is different from the steady-state hysteresis phenomenon, is discovered.
$\mathrm{RR} \rightarrow \mathrm{MR} $), occurs earlier than one would expect when the shock reflects from a single cylindrical convex surface. Furthermore, the hysteresis is observed at incident-shock-wave Mach numbers smaller than those at which the dual-solution domain starts, which is the minimal value for obtaining hysteresis in steady and pseudo-steady flows. The existence of a non-stationary hysteresis phenomenon, which is different from the steady-state hysteresis phenomenon, is discovered.