Published online by Cambridge University Press: 12 September 2013
Small-amplitude perturbations are governed by the linearized Navier–Stokes equations, which are, for a parallel or nearly parallel shear flow, customarily reduced to the Orr–Sommerfeld (O-S) and Squire equations. In this paper, we consider continuous spectra (CS) of the O-S and Squire operators for the Blasius and asymptotic suction boundary layers, and address the issue of whether and when continuous modes can represent free-stream vortical disturbances and their entrainment into the shear layer. For the Blasius boundary layer, we highlight two particular properties of the CS: (i) the eigenfunction of a continuous mode simultaneously consists of two components with wall-normal wavenumbers 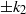 $\pm {k}_{2} $, a phenomenon which we refer to as ‘entanglement of Fourier components’; and (ii) for low-frequency disturbances the presence of the boundary layer forces the streamwise velocity in the free stream to take a much larger amplitude than those of the transverse velocities. Both features appear to be non-physical, and cast some doubt about the appropriateness of using CS to characterize free-stream vortical disturbances and their entrainment into the boundary layer, a practice that has been adopted in some recent studies of bypass transition. A high-Reynolds-number asymptotic description of continuous modes and entrainment is present, and it shows that the entanglement is a result of neglecting non-parallelism, which has a leading-order effect on the entrainment. When this effect is included, entanglement disappears, and moreover the streamwise velocity is significantly amplified in the edge layer when
$\pm {k}_{2} $, a phenomenon which we refer to as ‘entanglement of Fourier components’; and (ii) for low-frequency disturbances the presence of the boundary layer forces the streamwise velocity in the free stream to take a much larger amplitude than those of the transverse velocities. Both features appear to be non-physical, and cast some doubt about the appropriateness of using CS to characterize free-stream vortical disturbances and their entrainment into the boundary layer, a practice that has been adopted in some recent studies of bypass transition. A high-Reynolds-number asymptotic description of continuous modes and entrainment is present, and it shows that the entanglement is a result of neglecting non-parallelism, which has a leading-order effect on the entrainment. When this effect is included, entanglement disappears, and moreover the streamwise velocity is significantly amplified in the edge layer when 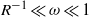 ${R}^{- 1} \ll \omega \ll 1$, where
${R}^{- 1} \ll \omega \ll 1$, where 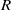 $R$ is the Reynolds number based on the local boundary-layer thickness. For the asymptotic suction boundary layer, which is an exactly parallel flow, both temporal and spatial CS may be defined mathematically. However, at a finite
$R$ is the Reynolds number based on the local boundary-layer thickness. For the asymptotic suction boundary layer, which is an exactly parallel flow, both temporal and spatial CS may be defined mathematically. However, at a finite 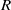 $R$ neither of them represents the physical process of free-stream vortical disturbances penetrating into the boundary layer. The latter must instead be characterized by a peculiar type of continuous modes whose eigenfunctions increase exponentially with the distance from the wall. In the limit
$R$ neither of them represents the physical process of free-stream vortical disturbances penetrating into the boundary layer. The latter must instead be characterized by a peculiar type of continuous modes whose eigenfunctions increase exponentially with the distance from the wall. In the limit 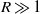 $R\gg 1$, all three types of CS are identical at leading order, and hence can be used to represent free-stream vortical disturbances and their entrainment. Low-frequency disturbances are found to generate a large-amplitude streamwise velocity in the boundary layer, which is reminiscent of longitudinal streaks.
$R\gg 1$, all three types of CS are identical at leading order, and hence can be used to represent free-stream vortical disturbances and their entrainment. Low-frequency disturbances are found to generate a large-amplitude streamwise velocity in the boundary layer, which is reminiscent of longitudinal streaks.