Motivated by drag-based propulsion of crinoids, the shape reconfiguration of a feather-like elastic structure under both steady and unsteady translational motions is investigated. The simplified elastic structure consists of a centre rod to which numerous side flaps are attached by elastic hinges. These side flaps fold in only one direction to realize a dramatic reduction in the area of the structure during the recovery stroke. Compared with experimental measurements, analytical methods developed to couple the dynamics of the centre rod and the side flaps successfully predict the drag force and three-dimensional reconfiguration of the elastic structure during both power and recovery strokes. A dimensionless speed given by the ratio of inertial fluid force to elastic bending force is proposed for the coupled deflections of the centre rod and side flaps, and is found to determine primarily the reconfiguration of the elastic structure. A reconfiguration number defined specifically for our model provides an appropriate characterization of the effect of side-flap folding on drag force reduction. Moreover, the ratio of drag forces between the power and recovery strokes is evaluated to find model conditions for the optimal force ratio.

The preference for particles to accumulate at specific regions in the near-wall part is a widely observed phenomenon in wall-bounded turbulence. Unlike small particles more frequently found in low-speed streaks, finite-size particles can accumulate in either low-speed or high-speed streaks. However, mechanisms and influencing factors leading to the different preferential concentration locations still need to be clarified. The present study conducts particle-resolved direct numerical simulations of particle-laden turbulent channel flows to provide a better understanding of this seemingly puzzling behaviour of preferential accumulation. These simulations cover different particle-to-fluid density ratios, particle volume fractions, particle sizes and degrees of sedimentation intensity. We find that the large particle size is the crucial factor that results in particles accumulating in high-speed streaks. Large particles not only are difficult to be conveyed by the quasi-streamwise vortices to low-speed streaks but also can escape from the near-wall region before moving spanwisely out from high-speed streaks. The sedimentation effect allows particles to gather closer to the channel wall and stay longer in the near-wall regions, reinforcing the sweeping mechanism of quasi-streamwise vortices that transport particles from high- to low-speed streaks. As a result, sedimenting particles tend to accumulate in the low-speed streaks.

This work presents the first experimental characterization of the flow field in the vicinity of periodically spaced discrete roughness elements (DRE) in a swept wing boundary layer. The time-averaged velocity fields are acquired in a volumetric domain by high-resolution dual-pulse tomographic particle tracking velocimetry. Investigation of the stationary flow topology indicates that the near-element flow region is dominated by high- and low-speed streaks. The boundary layer spectral content is inferred by spatial fast Fourier transform (FFT) analysis of the spanwise velocity signal, characterizing the chordwise behaviour of individual disturbance modes. The two signature features of transient growth, namely algebraic growth and exponential decay, are identified in the chordwise evolution of the disturbance energy associated with higher harmonics of the primary stationary mode. A transient decay process is instead identified in the near-wake region just aft of each DRE, similar to the wake relaxation effect previously observed in two-dimensional boundary layer flows. The transient decay regime is found to condition the onset and initial amplitude of modal crossflow instabilities. Within the critical DRE amplitude range (i.e. affecting boundary layer transition without causing flow tripping) the transient disturbances are strongly receptive to the spanwise spacing and diameter of the elements, which drive the modal energy distribution within the spatial spectra. In the super-critical amplitude forcing (i.e. causing flow tripping) the near-element stationary flow topology is dominated by the development of a high-speed and strongly fluctuating region closely aligned with the DRE wake. Therefore, elevated shears and unsteady disturbances affect the near-element flow development. Combined with the harmonic modes transient growth these instabilities initiate a laminar streak structure breakdown and a bypass transition process.

The Reynolds number dependent flow resistance of heterogeneous rough surfaces is largely unknown at present. The present work provides novel reference data for spanwise-alternating sandpaper strips as one idealised case of a heterogeneous rough surface. Experimental data are presented and analysed in direct comparison with drag measurements of homogeneous sandpaper surfaces and numerical simulations. Based on the homogeneous roughness data, the related challenges and sensitivities for the evaluation of roughness functions from experiments and simulations are discussed. A hydraulic channel height is suggested as an alternative measure for the drag impact of rough surfaces in internal flows. For the investigated heterogeneous roughness, it is found that turbulent flow does not exhibit a fully rough flow behaviour, indicating that the assignment of an equivalent sand grain height as commonly applied for homogeneous roughness is not possible. A prediction of the drag behaviour of rough strips based on an average between rough and smooth drag curves appears promising, but requires further refinement to capture the impact of turbulent secondary flows and spatial transients linking smooth and rough surface parts. While turbulent secondary flow induced by the roughness strips yield significant spanwise variation of the mean velocity profile for the investigated rough strips, we show that the spanwise averaged velocity profiles collapse reasonably well with a smooth or homogeneous rough wall flow. This allows to extract a global roughness function from the spanwise averaged flow field in good agreement with the one deduced from global pressure drop measurements.

We numerically investigate turbulent Rayleigh–Bénard convection with gas bubbles attached to the hot plate, mimicking a core feature in electrolysis, catalysis or boiling. The existence of bubbles on the plate reduces the global heat transfer due to the much lower thermal conductivity of gases as compared with liquids and changes the structure of the boundary layers. The numerical simulations are performed in three dimensions at Prandtl number 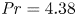$\mbox{Pr}=4.38$ (water) and Rayleigh number 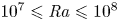$10^7\leqslant \mbox{Ra}\leqslant 10^8$. For simplicity, we assume the bubbles to be equally sized and having pinned contact lines. We vary the total gas-covered area fraction 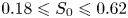$0.18 \leqslant S_0 \leqslant 0.62$, the relative bubble height 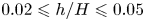$0.02\leqslant h/H \leqslant 0.05$ (where 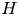$H$ is the height of the Rayleigh–Bénard cell), the bubble number 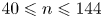$40 \leqslant n \leqslant 144$ and their spatial distribution. In all cases, asymmetric temperature profiles are observed, which we quantitatively explain based on the heat flux conservation at each horizontal section. We further propose the idea of using an equivalent single-phase set-up to mimic the system with attached bubbles. Based on this equivalence, we can calculate the heat transfer. Without introducing any free parameter, the predictions for the Nusselt number, the upper and lower thermal boundary layer thicknesses and the mean centre temperature agree well with the numerical results. Finally, our predictions also work for the cases with much larger 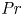$\mbox{Pr}$ (e.g. 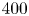$400$), which indicates that our results can also be applied to predict the mass transfer in water electrolysis with bubbles attached to the electrode surface or in catalysis.

Multigrain/polydispersity has a significant impact on turbidity current (TC). Despite the fact that several researches have looked into this effect, the impact of the fluid–particle interactions is not fully understood. Motivated by this, we employ the Eulerian–Lagrangian computational fluid dynamics–discrete element method model to investigate the dynamics of the bidisperse lock-exchange TC. Results show that, because the coarse particles will settle faster and stop moving forward, the two phases of bidisperse transport and fine component transport can be distinguished in the evolution of the bidisperse TC. During the bidisperse transport stage, the upper interface of each component is primarily determined by their own settling and transport characteristics and does not strongly depend on the relative fine particle volume fraction $\phi _F$. Fine particles are primarily responsible for the vortical structures near the upper interface of the TC head, and the increase of $\phi _F$ promotes their streamwise development. In comparison, fragmented vortical coherent structures are closely related to the presence of coarse particles, which can be seen in the lower layers. Bidisperse segregation alters the collision process between dispersed phases, which differs from monodisperse TC. The collisions and segregation-induced flow establish interconnections between the two dispersed phases. In the latter stage, the transport of fine particles is inhibited by both the lift force and the contact force produced by the collision with the deposited materials. As $\phi _F$ rises, the negative contact force weakens, and its change is essentially balanced by the rise in negative lift force.

Extensive studies have focused on the self-propulsion of a droplet in a viscous environment driven by the Marangoni effect in the absence of inertial effects. In order to capture the influence of inertia on the self-propulsion of a droplet, we use the singular perturbation solution for small but finite Reynolds number ($Re$) flow past a spherical droplet with inhomogeneous surface tension. We calculate the swimming speed and the corresponding flow fields generated by the droplet in an axisymmetric unbounded medium at $O(Re^2)$. The present results reveal how the choice of the stress parameter $\sigma$, which is the ratio of the first two modes of the induced stress field, distinguishes between the different swimming styles, and determines the role of inertia on the swimming speed, energy expenditure and swimming efficiency of the droplet. Inertia enhances the swimming speed and the associated swimming efficiency of the droplet by abating the energy expenditure. It is striking to observe how a droplet swimmer with $\sigma <0$ has a competitive advantage over a rigid squirmer with an equivalent surface activity due to the existence of an internal flow. We independently treat the potential influence of the viscosity ratio on the swimming properties of the droplet at finite $Re$. Additionally, using linear stability analysis, we provide insights into the stability of the estimated migration velocity at $O(Re)$. We argue that the droplet achieves a distinct stable equilibrium velocity, which occurs due to the inertial effect of the surrounding medium.

Theoretical analysis and numerical results have shown that frequency lock-in in vortex-induced vibration (VIV) is caused by the instability of the structural mode rather than a resonant response to external excitations. However, there is a lack of experimental evidence supporting relevant theoretical research findings. This study investigates VIV suppression with a passive modal controller (PMC) for a circular cylinder at Reynolds numbers $Re = 60$ and $Re = 40$, using experiments to distinguish the effects of stable and unstable wake modes. Comparative analysis before and after the implementation of the PMC reveals significant reduction in the vibration amplitude and the disappearance of the lock-in phenomenon at $Re = 60$. The vibration frequency closely follows the vortex shedding frequency after control, while dynamic mode decomposition of the flow field indicates that the wake mode is dominant. For $Re = 40$, the vibration is eliminated and the flow becomes steady. Additionally, the root loci of the coupled system are investigated before and after the PMC implementation via linear stability analysis. The results indicate that the PMC can alter the dynamic characteristics of the original system, causing the structural mode and PMC mode to couple when approaching the PMC frequency. Then, the interaction typically improves the stability of the structural mode. Finally, a parametric study is conducted in the experiment, as well as a linear stability analysis. The study provides experimental evidence that stability control of the structural mode is the key to suppressing VIV and eliminating the lock-in phenomenon.

Seafloor roughness profoundly influences the pattern and dynamics of large-scale oceanic flows. However, these kilometre-scale topographic patterns are unresolved by global numerical Earth system models and will remain subgrid for the foreseeable future. To properly represent the effects of small-scale bathymetry in analytical and coarse-resolution numerical models, we develop the stratified ‘sandpaper’ theory of flow–topography interaction. This model, which is based on the multilayer shallow-water framework, extends its barotropic antecedent to stratified flows. The proposed theory is successfully tested on the configuration representing the interaction of a zonal current with a corrugated cross-flow ridge.

This study introduces an analytical solution for the laminar entrance flow in circular pipes, aiming to confirm the occurrence of velocity overshoot. Velocity overshoot is characterised by the maximum axial velocity appearing near the pipe wall instead of the central axis. Similar to the previous studies, the analytical solution is derived from the parabolised Navier–Stokes equation; however, the specific approach used in linearising the momentum equation has not been attempted before. The accuracy of this analytical solution has been verified through a comprehensive comparison with various published experimental data. The existence of velocity overshoot at a short distance from the inlet, which is evident in numerous numerical calculations based on the full Navier–Stokes equations and corroborated by recent magnetic resonance (MR) velocimetry experiments, is identified analytically for the first time. The parabolised Navier–Stokes equation has inherent self-similarity with respect to the Reynolds number, implying that $Re$ is incorporated into the dimensionless variables rather than serving as an independent flow parameter. According to both MR velocimetry measurements and the present analytical solution, the self-similarity is not valid immediately following the pipe inlet, and this becomes more evident as $Re$ decreases; hence, the analytical solution derived from the parabolised Navier–Stokes equation cannot accurately predict the evolution of the velocity profile within this region near the pipe inlet.

A form of skin-friction drag decomposition is given based on the velocity–vorticity correlations, $\langle v\omega _z\rangle$ and $\langle -w\omega _y\rangle$, which represent the advective vorticity transport and vortex stretching, respectively. This identity provides a perspective to understand the mechanism of skin-friction drag generation from vortical motions and it has better physical interpretability compared with some previous studies. The skin-friction coefficients in incompressible turbulent channel flows at friction Reynolds numbers from 186 to 2003 are divided with this velocity–vorticity correlation-based identity. We mainly focus on the Reynolds number effects on the contributing terms, their scale-dependence and quadrant characteristics. Results show that the contributing terms and their proportions exhibit similarities and the same peak locations across the wall layer. For the first time, we find that the positive and negative regions in the spanwise pre-multiplied spectra of the turbulent inertia ($\langle v'\omega _z'\rangle +\langle -w'\omega _y'\rangle$) can be separated with a universal linear relationship of $\lambda _z^+=3.75y^+$. The linear relationship is adopted as the criterion to investigate the scale dependence of the velocity–vorticity coupling structures. It reveals that the negative and positive structures dominate the generation of friction drag associated with the advective vorticity transport and vortex stretching, respectively. Moreover, quadrant analyses of the velocity–vorticity correlations are performed to further examine the friction drag generation related to different quadrant motions.

We explore the transition to chaos in a prototypical hydrodynamic oscillator, namely a globally unstable low-density jet subjected to external time-periodic forcing. As the forcing strengthens at an off-resonant frequency, we find that the jet exhibits a sequence of nonlinear states: period-1 limit cycle $\rightarrow $ quasiperiodicity $\rightarrow$ intermittency $\rightarrow$ low-dimensional chaos. We show that the intermittency obeys type-II Pomeau–Manneville dynamics by analysing the first return map and the scaling properties of the quasiperiodic lifetimes between successive chaotic epochs. By providing experimental evidence of the type-II intermittency route to chaos in a globally unstable jet, this study reinforces the idea that strange attractors emerge via universal mechanisms in open self-excited flows, facilitating the development of instability control strategies based on chaos theory.

We develop and analyse a continuum model of two-phase slurry dynamics for planetary cores. Mixed solid–liquid slurry regions may be ubiquitous in the upper cores of small terrestrial bodies and have also been invoked to explain anomalous seismic structure in the F-layer at the base of Earth's liquid iron core. These layers are expected to influence the dynamics and evolution of planetary cores, including their capacity to generate global magnetic fields; however, to date, models of two-phase regions in planetary cores have largely ignored the complex fluid dynamics that arises from interactions between phases. As an initial application of our model, and to focus on fundamental fluid dynamical processes, we consider a non-rotating and non-magnetic slurry comprised of a single chemical component with a temperature that is tied to the liquidus. We study one-dimensional solutions in a configuration set up to mimic Earth's F-layer, varying gravitational strength $R$, the solid/liquid viscosity ratio $\lambda _{\mu }$ and the interaction parameter $K$, which measures friction between the phases. We develop scalings describing behaviour in the limit $R \gg 1$ and $\lambda _{\mu } \gg 1$, which are in excellent agreement with our numerical results. Application to Earth's core, where $R \sim 10^{28}$ and $\lambda _{\mu } \sim 10^{22}$, suggests that a pure iron slurry F-layer would contain a mean solid fraction of at most 5 %.

We derive reduced models for extrusion problems where it is necessary to account for fluid compressibility. We consider the two-dimensional extensional flow of a compressible viscous fluid and discuss two specific applications: weakly compressible fluids and bubbly liquid–gas mixtures that behave as a single compressible fluid. The mathematical model we present consists of equations for conservation of mass, conservation of momentum and a closure relationship between the pressure and density. The most substantial differences between compressible extrusion problems is in the closure relationship. By integrating the conservation equations across the fluid cross-section and exploiting a slender aspect ratio, we derive reduced equations for conservation of mass and conservation of momentum in the direction of flow. The reduced system of equations relating cross-sectionally averaged quantities is closed by a relationship between the averaged pressure and density, which will differ substantially depending on the application. We demonstrate the utility of a reduced model for both the weakly compressible fluid and bubbly mixture applications; namely, in providing valuable quantitative insights without needing to solve a complicated free-boundary problem.

The theory of transient growth describes how linear mechanisms can cause temporary amplification of disturbances even when the linearized system is asymptotically stable as defined by its eigenvalues. This growth is traditionally quantified by finding the initial disturbance that generates the maximum response at the peak time of its evolution. However, this can vastly overstate the growth of a real disturbance. In this paper, we introduce a statistical perspective on transient growth that models statistics of the energy amplification of the disturbances. We derive a formula for the mean energy amplification and spatial correlation of the growing disturbance in terms of the spatial correlation of the initial disturbance. The eigendecomposition of the correlation provides the most prevalent structures, which are the statistical analogue of the standard left singular vectors of the evolution operator. We also derive accurate confidence bounds on the growth by approximating the probability density function of the energy. Applying our analysis to Poiseuille flow yields a number of observations. First, the mean energy amplification is often drastically smaller than the maximum. In these cases, it is exceedingly unlikely to achieve near-optimal growth due to the exponential behaviour observed in the probability density function. Second, the characteristic length scale of the initial disturbances has a significant impact on the expected growth, with large-scale initial disturbances growing orders of magnitude more than small-scale ones. Finally, while the optimal growth scales quadratically with Reynolds number, the mean energy amplification scales only linearly for certain reasonable choices of the initial correlation.

Analysis of the classic problem of shallow film flow on an inclined plane is revisited for a Brownian suspension. The particle phase, considered in a two-fluid model, is predicted to cause pronounced changes to the instability characteristics of the flow. These are due to an indirect effect of the non-Newtonian rheology, with the normal stresses causing migration and a viscosity stratification which strongly alters the base state from its Newtonian counterpart. Both the short- and long-wavelength inertial stability boundaries are altered, and, more strikingly, an instability at zero Reynolds number is found.

We investigate with a two-fluid model the convections developing in a gas–liquid two-phase flow, which consists of a horizontal liquid layer subject to the injection of monodisperse gas bubbles at the bottom. The convections develop in either whole- or multi-layered modes, once the gas injection flux exceeds a critical value (Nakamura et al., Phys. Rev. E, vol. 102, 2020, 053102). We determine the nonlinear evolution of these modes of flows with varying injection flux and find that the whole- and multi-layered modes develop through subcritical and supercritical bifurcations, respectively. The formation of gas plumes is observed in both cases when the nonlinearity is significant. Examining energy transfer from base to perturbation flows, we show that the lift forces on bubbles play a key role in the bifurcations. While they impede the convections in both subcritical and supercritical bifurcations at weak nonlinearity, the lift forces turn to driving the convections in the subcritical bifurcation as nonlinearity increases.