Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T14:27:10.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation analysis of bubble-induced convection in a horizontal liquid layer: role of forces on bubbles

Published online by Cambridge University Press:  27 July 2021

Kotaro Nakamura Open the ORCID record for Kotaro Nakamura [Opens in a new window] ,
Harunori N. Yoshikawa Open the ORCID record for Harunori N. Yoshikawa [Opens in a new window] ,
Yuji Tasaka Open the ORCID record for Yuji Tasaka [Opens in a new window]  and
Yuichi Murai Open the ORCID record for Yuichi Murai [Opens in a new window]
Kotaro Nakamura*
Affiliation:
Laboratory for Flow Control, Hokkaido University, Sapporo 060-8628, Japan
Harunori N. Yoshikawa
Affiliation:
Université Côte d'Azur, CNRS, Institut de Physique de Nice, 06100 Nice, France
Yuji Tasaka
Affiliation:
Laboratory for Flow Control, Hokkaido University, Sapporo 060-8628, Japan
Yuichi Murai
Affiliation:
Laboratory for Flow Control, Hokkaido University, Sapporo 060-8628, Japan
*
Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

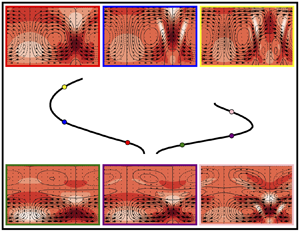
We investigate with a two-fluid model the convections developing in a gas–liquid two-phase flow, which consists of a horizontal liquid layer subject to the injection of monodisperse gas bubbles at the bottom. The convections develop in either whole- or multi-layered modes, once the gas injection flux exceeds a critical value (Nakamura et al., Phys. Rev. E, vol. 102, 2020, 053102). We determine the nonlinear evolution of these modes of flows with varying injection flux and find that the whole- and multi-layered modes develop through subcritical and supercritical bifurcations, respectively. The formation of gas plumes is observed in both cases when the nonlinearity is significant. Examining energy transfer from base to perturbation flows, we show that the lift forces on bubbles play a key role in the bifurcations. While they impede the convections in both subcritical and supercritical bifurcations at weak nonlinearity, the lift forces turn to driving the convections in the subcritical bifurcation as nonlinearity increases.

JFM classification

Convection: Buoyancy-driven instability Multiphase and Particle-laden Flows: Gas/liquid flow Nonlinear Dynamical Systems: Bifurcation
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , R4
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Department of Mechanical Engineering, National Institute of Technology, Ube College, Ube 755-8555, Japan.

References

REFERENCES

Agrawal, N., Choueiri, G.H. & Hof, B. 2019 Transition to turbulence in particle laden flows. Phys. Rev. Lett. 122 (11), 114502.CrossRefGoogle ScholarPubMed
Albaalbaki, B. & Khayat, R.E. 2011 Pattern selection in the thermal convection of non-Newtonian fluids. J. Fluid Mech. 668, 500–550.CrossRefGoogle Scholar
Benouared, O., Mamou, M. & Messaoudene, N.A. 2014 Numerical nonlinear analysis of subcritical Rayleigh–Bénard convection in a horizontal confined enclosure filled with non-Newtonian fluids. Phys. Fluids 26, 073101.CrossRefGoogle Scholar
Bouteraa, M., Nouar, C., Plaut, E., Metivier, C. & Klack, A. 2015 Weakly nonlinear analysis of Rayleigh–Bénard convection in shear-thinning fluids: nature of the bifurcation and pattern selection. J. Fluid Mech. 767, 696–734.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Climent, E. & Magnaudet, J. 1999 Large-scale simulations of bubble-induced convection in a liquid layer. Phys. Rev. Lett. 82 (24), 4827.CrossRefGoogle Scholar
Curbelo, J. & Mancho, A.M. 2014 Spectral numerical schemes for time-dependent convection with viscosity dependent on temperature. Commun. Nonlinear Sci. Numer. Simul. 19, 538–553.CrossRefGoogle Scholar
Deguchi, K. & Nagata, M. 2011 Bifurcations and instabilities in sliding Couette flow. J. Fluid Mech. 678, 156–178.CrossRefGoogle Scholar
Dijkstra, H., et al. 2014 Numerical bifurcation methods and their application to fluid dynamics: analysis beyond simulation. Commun. Comput. Phys. 15 (1), 1–45.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 2010 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Druzhinin, O.A. & Elghobashi, S. 1998 Direct numerical simulation of bubble-laden turbulent flows using the two fluid formulation. Phys. Fluids 10 (3), 685–697.CrossRefGoogle Scholar
Hadamard, J. 1911 Mouvement permanent lent d'une sphere liquid et visqueuse dans un liquide visqueux. C. R. Acad. Sci. 152, 1735–1738.Google Scholar
Hogendoorn, W. & Poelma, C. 2018 Particle-laden pipe flows at high volume fractions show transition without puffs. Phys. Rev. Lett. 121 (19), 194501.CrossRefGoogle ScholarPubMed
Iga, K. & Kimura, R. 2007 Convection driven by collective buoyancy of microbubbles. Fluid Dyn. Res. 39 (1–3), 68–97.CrossRefGoogle Scholar
Kang, C., Yoshikawa, H.N. & Mirbod, P. 2021 Onset of thermal convection in non-colloidal suspensions. J. Fluid Mech. 915, A128.CrossRefGoogle Scholar
Levich, V.G. 1962 Physicochemical Hydrodynamics. Prentice-Hall.Google Scholar
Lohse, D. 2018 Bubble puzzles: from fundamentals to applications. Phys. Rev. Fluids 3 (11), 110504.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.CrossRefGoogle Scholar
Mudde, R.F. 2005 Gravity-driven bubbly flows. Annu. Rev. Fluid Mech. 37, 393–423.CrossRefGoogle Scholar
Nakamura, K., Yoshikawa, H.N., Tasaka, Y. & Murai, Y. 2020 Linear stability analysis of bubble-induced convection in a horizontal liquid layer. Phys. Rev. E 102, 053102.CrossRefGoogle Scholar
Nield, D.A. 1975 The onset of transient convective instability. J. Fluid Mech. 71 (3), 441–454.CrossRefGoogle Scholar
Ogura, Y. & Kondo, H. 1970 A linear stability of convective motion in a thermally unstable layer below a stable region. J. Met. Soc. Japan 48 (3), 204–216.CrossRefGoogle Scholar
Parmentier, E.M. 1978 A study of thermal convection in non-Newtonian fluids. J. Fluid Mech. 84 (1), 1–11.CrossRefGoogle Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50, 25–48.CrossRefGoogle Scholar
Ruzicka, M.C. 2013 On stability of a bubble column. Chem. Engng Res. Des. 91 (2), 191–203.CrossRefGoogle Scholar
Ruzicka, M.C. & Thomas, N.H. 2003 Buoyancy-driven instability of bubbly layers: analogy with thermal convection. Intl J. Multiphase Flow 29 (2), 249–270.CrossRefGoogle Scholar
Rybczynski, W. 1911 Uber die fortschreitende Bewegung einer flussigen Kugel in einem zahen Medium. Bull. Acad. Sci. 1, 40–46.Google Scholar
Solomatov, V.S. 2012 Localized subcritical convective cells in temperature-dependent viscosity fluids. Phys. Earth Planet. Inter. 200–201, 63–71.CrossRefGoogle Scholar
Sommerfeld, M. 2004 Bubbly Flows: Analysis, Modelling and Calculation. Springer.CrossRefGoogle Scholar
Stokes, G.G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. IX, 8.Google Scholar