1. Introduction
Open-jet flows are integral to a wide range of technological and natural processes. As such, their spatiotemporal stability and nonlinear dynamics have been widely studied (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Schmid & Henningson Reference Schmid and Henningson2001). In the absence of counterflow, a jet whose density is similar to that of its surroundings is dominated by local convective instability, behaving as a spatial amplifier of extrinsic disturbances (Huerre & Monkewitz Reference Huerre and Monkewitz1990). By contrast, a jet whose density is below a critical value can develop a large enough region of local absolute instability to become globally unstable, behaving as a self-excited oscillator with an intrinsic hydrodynamic mode (Chomaz, Huerre & Redekopp Reference Chomaz, Huerre and Redekopp1988; Monkewitz et al. Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Hallberg & Strykowski Reference Hallberg and Strykowski2006; Lesshafft & Marquet Reference Lesshafft and Marquet2010; Coenen et al. Reference Coenen, Lesshafft, Garnaud and Sevilla2017; Chakravarthy, Lesshafft & Huerre Reference Chakravarthy, Lesshafft and Huerre2018; Nair, Deohans & Vinoth Reference Nair, Deohans and Vinoth2022). In nonlinear dynamics, this can be viewed as a transition from a fixed point to a limit cycle, which can occur via a supercritical or subcritical Hopf bifurcation (Zhu, Gupta & Li Reference Zhu, Gupta and Li2017; Lee et al. Reference Lee, Zhu, Li and Gupta2019; Zhu, Gupta & Li Reference Zhu, Gupta and Li2019). The self-excited flow oscillations arising from global instability can be destructive – especially when they interact constructively with acoustic, structural or other hydrodynamic modes – necessitating control action.
Previous studies have shown that time-periodic acoustic forcing is effective in controlling both the frequency and amplitude of the self-excited oscillations of a globally unstable jet (Sreenivasan, Raghu & Kyle Reference Sreenivasan, Raghu and Kyle1989; Kyle & Sreenivasan Reference Kyle and Sreenivasan1993). Such control action can produce a range of synchronisation phenomena, including quasiperiodicity, phase trapping and locking, asynchronous and synchronous quenching, as well as saddle-node and inverse Neimark–Sacker bifurcations (Li & Juniper Reference Li and Juniper2013a,Reference Li and Juniperb; Kushwaha et al. Reference Kushwaha, Worth, Dawson, Gupta and Li2022). Surprisingly, however, the emergence of deterministic chaos – a fundamental concept in nonlinear dynamics – has yet to be established in a globally unstable jet, irrespective of the type of forcing.
Identifying the routes to chaos is key to gaining a better understanding of the universal mechanisms and symmetry-breaking processes that govern the transition from ordered to complex states, such as turbulence (Manneville Reference Manneville2010). It can also facilitate theoretical efforts to model, predict and control the behaviour of open self-excited flows (Huerre & Monkewitz Reference Huerre and Monkewitz1990). In general, a nonlinear dynamical system can become chaotic via multiple universal routes (Ott Reference Ott2002). Since the 1980s, three routes have received broad attention.
(i) Along the period-doubling route, varying a control parameter causes an existing periodic orbit to lose stability and be replaced by a new attracting periodic orbit of half the original frequency. This process repeats indefinitely, resulting in a period-doubling cascade that forms a self-similar structure in the bifurcation map (Feigenbaum Reference Feigenbaum1978).
(ii) Along the Ruelle–Takens–Newhouse route, three Hopf bifurcations occur successively, yielding a quasiperiodic (torus,
 $\mathbb {T}^3$) attractor with three incommensurable frequencies. Such an attractor is unstable to even the smallest perturbations, transforming into a chaotic attractor by stretching and folding (Newhouse, Ruelle & Takens Reference Newhouse, Ruelle and Takens1978).
$\mathbb {T}^3$) attractor with three incommensurable frequencies. Such an attractor is unstable to even the smallest perturbations, transforming into a chaotic attractor by stretching and folding (Newhouse, Ruelle & Takens Reference Newhouse, Ruelle and Takens1978).(iii) Along the intermittency route, chaotic epochs emerge intermittently against a background of regular dynamics, even when the system parameters are fixed and free of substantial noise. Varying a control parameter causes the lifetime and frequency of the chaotic epochs to increase, eventually leading to a state of sustained chaos. In early studies of dissipative dynamical systems, Pomeau & Manneville (Reference Pomeau and Manneville1980) discovered three possible types of intermittency leading to chaos: type I corresponding to a saddle-node bifurcation, type II corresponding to a subcritical Hopf bifurcation, and type III corresponding to an inverse period-doubling bifurcation. Many additional types, such as crisis-induced intermittency and on–off intermittency, have since been discovered (Ott Reference Ott2002).
In fluid mechanics, all three of these classic routes to chaos have been observed, albeit mostly in closed flows (e.g. Rayleigh–Bénard convection; Gollub & Benson Reference Gollub and Benson1980) and in open-wake flows (Olinger & Sreenivasan Reference Olinger and Sreenivasan1988; Pasche, Avellan & Gallaire Reference Pasche, Avellan and Gallaire2018). To date, only a few studies have reported definitive evidence of chaos in open-jet flows. Crucially, that evidence is largely limited to globally stable jets dominated by local convective instability. Such jets are exceptionally sensitive to extrinsic disturbances, making it challenging to distinguish between spatially amplified stochastic noise and low-dimensional deterministic chaos due to the flow itself (Huerre & Monkewitz Reference Huerre and Monkewitz1990). Nevertheless, experimental and numerical evidence of chaos has been identified in globally stable equidensity jets subjected to external periodic forcing (Bonetti & Boon Reference Bonetti and Boon1989) and to Reynolds number variations (Danaila, Dušek & Anselmet Reference Danaila, Dušek and Anselmet1998). In both instances, the chaos was attributed to the collapse of helical flow structures in the near field of the jet. Moreover, Broze & Hussain (Reference Broze and Hussain1996) observed a transition to low-dimensional chaos via type-II intermittency in a globally stable equidensity jet subjected to external periodic forcing. By contrast, the existence of chaos in a globally unstable jet, which hosts a natural hydrodynamically self-excited mode (Monkewitz et al. Reference Monkewitz, Bechert, Barsikow and Lehmann1990; Hallberg & Strykowski Reference Hallberg and Strykowski2006), has yet to be rigourously established. The sole evidence to date, from the seminal experiments of Sreenivasan et al. (Reference Sreenivasan, Raghu and Kyle1989), is merely suggestive, as it only hints at the possibility of chaos based on analogies between self-excited wakes and jets. Importantly, the routes to chaos in a globally unstable jet have yet to be identified.
In this experimental study, we report the first conclusive evidence of chaos in a globally unstable jet, and show that the chaos arises via type-II intermittency belonging to the class of Pomeau & Manneville (Reference Pomeau and Manneville1980). By providing new insight into how strange attractors emerge in open self-excited flows, this study creates new opportunities for the development of instability control strategies based on chaos theory (Boccaletti et al. Reference Boccaletti, Grebogi, Lai, Mancini and Maza2000). Below, we introduce our experimental set-up (§ 2), present evidence of the type-II intermittency route to chaos (§ 3), and conclude with the implications of this discovery (§ 4).
2. Experimental set-up
We generate a globally unstable jet by discharging gaseous helium into ambient air (![]() $296$ K,
$296$ K, ![]() $1$ bar) using the same experimental facility that was used in our previous studies on the nonlinear dynamics of low-density jets (Zhu et al. Reference Zhu, Gupta and Li2017; Lee et al. Reference Lee, Zhu, Li and Gupta2019; Zhu et al. Reference Zhu, Gupta and Li2019). Shown in figure 1(a), the facility consists of a nozzle assembly, a helium supply system, and electronics for data acquisition and external forcing. The nozzle assembly contains a convergent section (area ratio of 100:1) with a round outlet of diameter
$1$ bar) using the same experimental facility that was used in our previous studies on the nonlinear dynamics of low-density jets (Zhu et al. Reference Zhu, Gupta and Li2017; Lee et al. Reference Lee, Zhu, Li and Gupta2019; Zhu et al. Reference Zhu, Gupta and Li2019). Shown in figure 1(a), the facility consists of a nozzle assembly, a helium supply system, and electronics for data acquisition and external forcing. The nozzle assembly contains a convergent section (area ratio of 100:1) with a round outlet of diameter ![]() $D=6$ mm and extension length
$D=6$ mm and extension length ![]() $L=D$. For an axisymmetric jet in the incompressible inertial regime, the onset of global instability is known to be determined by three primary parameters (Hallberg & Strykowski Reference Hallberg and Strykowski2006; Coenen et al. Reference Coenen, Lesshafft, Garnaud and Sevilla2017; Chakravarthy et al. Reference Chakravarthy, Lesshafft and Huerre2018; Nair et al. Reference Nair, Deohans and Vinoth2022): (i) the jet Reynolds number,
$L=D$. For an axisymmetric jet in the incompressible inertial regime, the onset of global instability is known to be determined by three primary parameters (Hallberg & Strykowski Reference Hallberg and Strykowski2006; Coenen et al. Reference Coenen, Lesshafft, Garnaud and Sevilla2017; Chakravarthy et al. Reference Chakravarthy, Lesshafft and Huerre2018; Nair et al. Reference Nair, Deohans and Vinoth2022): (i) the jet Reynolds number, ![]() $Re \equiv \rho _j U_j D/ \mu _j$, where
$Re \equiv \rho _j U_j D/ \mu _j$, where ![]() $\rho _j$ and
$\rho _j$ and ![]() $\mu _j$ are the density and dynamic viscosity of the jet fluid, while
$\mu _j$ are the density and dynamic viscosity of the jet fluid, while ![]() $U_j$ is the jet centreline velocity; (ii) the jet-to-ambient density ratio,
$U_j$ is the jet centreline velocity; (ii) the jet-to-ambient density ratio, ![]() $S \equiv \rho _j/\rho _\infty$, where
$S \equiv \rho _j/\rho _\infty$, where ![]() $\rho_\infty$ is the density of the ambient fluid; and (iii) the transverse curvature,
$\rho_\infty$ is the density of the ambient fluid; and (iii) the transverse curvature, ![]() $D/\theta _0$, where
$D/\theta _0$, where ![]() $\theta _0$ is the initial momentum thickness. In this study, we focus on a parameter combination (
$\theta _0$ is the initial momentum thickness. In this study, we focus on a parameter combination (![]() $Re = 648$,
$Re = 648$, ![]() $S = 0.14$,
$S = 0.14$, ![]() $D/\theta _0 = 31.1$) just beyond the Hopf point, where an axisymmetric global mode exists at a natural frequency of
$D/\theta _0 = 31.1$) just beyond the Hopf point, where an axisymmetric global mode exists at a natural frequency of ![]() $f_n = 497 \pm 5$ Hz. This frequency, which corresponds to a Strouhal number of
$f_n = 497 \pm 5$ Hz. This frequency, which corresponds to a Strouhal number of ![]() $St = 0.23$ based on
$St = 0.23$ based on ![]() $D$ and
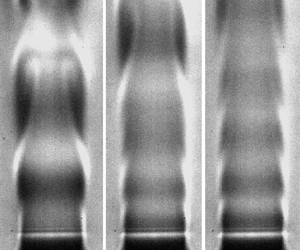
$D$ and ![]() $U_j$, is within 15 % of the universal scaling proposed by Hallberg & Strykowski (Reference Hallberg and Strykowski2006) through considerations of a viscous time scale and the centripetal acceleration generated by the streamwise curvature of the oscillating jet column. Figure 1(b) shows a schlieren snapshot of this global mode, alongside an equivalent low-density jet without a global mode (figure 1c). In the former case, large-amplitude self-excited axisymmetric oscillations can be seen dominating the jet potential core.
$U_j$, is within 15 % of the universal scaling proposed by Hallberg & Strykowski (Reference Hallberg and Strykowski2006) through considerations of a viscous time scale and the centripetal acceleration generated by the streamwise curvature of the oscillating jet column. Figure 1(b) shows a schlieren snapshot of this global mode, alongside an equivalent low-density jet without a global mode (figure 1c). In the former case, large-amplitude self-excited axisymmetric oscillations can be seen dominating the jet potential core.

Figure 1. (a) Diagram of the experimental facility used to produce an axisymmetric jet of helium gas; MFC: mass flow controller. Also shown are schlieren snapshots of (b) a globally unstable jet at ![]() $Re = 648$ and (c) a globally stable jet at
$Re = 648$ and (c) a globally stable jet at ![]() $Re = 385$, both for
$Re = 385$, both for ![]() $S = 0.14$ and without external forcing. In the globally unstable jet (b), large-amplitude self-excited axisymmetric oscillations can be seen dominating the potential core.
$S = 0.14$ and without external forcing. In the globally unstable jet (b), large-amplitude self-excited axisymmetric oscillations can be seen dominating the potential core.
To induce chaotisation, we subject the globally unstable jet to axisymmetric acoustic forcing generated by a loudspeaker mounted at the base of a cylindrical settling chamber containing a honeycomb flow straightener (see figure 1a). The loudspeaker is driven by a time-periodic signal with a normalised frequency of ![]() $f_f/f_n \in [1.75, 1.81]$ and a normalised amplitude of
$f_f/f_n \in [1.75, 1.81]$ and a normalised amplitude of ![]() $\alpha \equiv A/A_c \in [0, 2.2]$, where
$\alpha \equiv A/A_c \in [0, 2.2]$, where ![]() $f_f$ is the forcing frequency,
$f_f$ is the forcing frequency, ![]() $A$ is the loudspeaker voltage and
$A$ is the loudspeaker voltage and ![]() $A_c = 299$ mV
$A_c = 299$ mV![]() $_\textrm {rms}$ is the critical voltage at the onset of intermittency. The significance of this specific range of forcing frequencies will be discussed later. At these forcing conditions, the root-mean-square velocity perturbations generated at the nozzle outlet are directly proportional to the loudspeaker voltage:
$_\textrm {rms}$ is the critical voltage at the onset of intermittency. The significance of this specific range of forcing frequencies will be discussed later. At these forcing conditions, the root-mean-square velocity perturbations generated at the nozzle outlet are directly proportional to the loudspeaker voltage: ![]() $u^\prime _{0,rms} = (2.8 \times 10^{-4}\ \textrm {m}\ \textrm {s}^{-1}\ \textrm {mV}_{rms}^{-1})A$. We monitor the jet response with a constant-temperature single-wire anemometer (Dantec 55P16) located inside the jet potential core, specifically at
$u^\prime _{0,rms} = (2.8 \times 10^{-4}\ \textrm {m}\ \textrm {s}^{-1}\ \textrm {mV}_{rms}^{-1})A$. We monitor the jet response with a constant-temperature single-wire anemometer (Dantec 55P16) located inside the jet potential core, specifically at ![]() $(x/D, r/D) = (1.5D, 0)$, where
$(x/D, r/D) = (1.5D, 0)$, where ![]() $x$ and
$x$ and ![]() $r$ are the streamwise and radial coordinates, respectively. At this sampling location, the jet dynamics is dictated by the wavemaker of the global mode, and the jet fluid (helium) concentration does not vary, enabling time traces of the local velocity
$r$ are the streamwise and radial coordinates, respectively. At this sampling location, the jet dynamics is dictated by the wavemaker of the global mode, and the jet fluid (helium) concentration does not vary, enabling time traces of the local velocity ![]() $u(t)$ to be extracted from a precalibration. We use a 16-bit data acquisition system (NI USB-6212) to digitise the anemometer voltage at
$u(t)$ to be extracted from a precalibration. We use a 16-bit data acquisition system (NI USB-6212) to digitise the anemometer voltage at ![]() $65\,536$ Hz, which exceeds
$65\,536$ Hz, which exceeds ![]() $100f_n$. We use a sampling duration of
$100f_n$. We use a sampling duration of ![]() $8$ s for most cases, but raise this to
$8$ s for most cases, but raise this to ![]() $60$ s for cases showing any signs of intermittency in order to obtain converged statistics. For more information on the experimental set-up, please see our previous studies (Zhu et al. Reference Zhu, Gupta and Li2017; Lee et al. Reference Lee, Zhu, Li and Gupta2019; Zhu et al. Reference Zhu, Gupta and Li2019).
$60$ s for cases showing any signs of intermittency in order to obtain converged statistics. For more information on the experimental set-up, please see our previous studies (Zhu et al. Reference Zhu, Gupta and Li2017; Lee et al. Reference Lee, Zhu, Li and Gupta2019; Zhu et al. Reference Zhu, Gupta and Li2019).
3. Results and discussion
3.1. Intermittency route to chaos
Li & Juniper (Reference Li and Juniper2013a,Reference Li and Juniperb) have shown that when a globally unstable jet is forced axially at an incommensurable frequency around ![]() $f_f/f_n = 1$, forced synchronisation can occur via two sequential transitions: (i) from a period-1 limit cycle to a
$f_f/f_n = 1$, forced synchronisation can occur via two sequential transitions: (i) from a period-1 limit cycle to a ![]() $\mathbb {T}^2$ quasiperiodic attractor through a Neimark–Sacker bifurcation; and then (ii) from the
$\mathbb {T}^2$ quasiperiodic attractor through a Neimark–Sacker bifurcation; and then (ii) from the ![]() $\mathbb {T}^2$ quasiperiodic attractor to a 1:1 synchronous orbit either through a saddle-node bifurcation, leading to phase locking, or through an inverse Neimark–Sacker bifurcation, leading to suppression.
$\mathbb {T}^2$ quasiperiodic attractor to a 1:1 synchronous orbit either through a saddle-node bifurcation, leading to phase locking, or through an inverse Neimark–Sacker bifurcation, leading to suppression.
In this study, we show that an alternative transition scenario can occur when ![]() $f_f$ is within a specific range between the natural mode and its second harmonic,
$f_f$ is within a specific range between the natural mode and its second harmonic, ![]() $f_f/f_n \in [1.75, 1.81]$. Figure 2 summarises this scenario for a representative case where
$f_f/f_n \in [1.75, 1.81]$. Figure 2 summarises this scenario for a representative case where ![]() $f_f/f_n=1.78$. As the forcing amplitude
$f_f/f_n=1.78$. As the forcing amplitude ![]() $\alpha$ increases, the jet transitions through four dynamical states: limit cycle
$\alpha$ increases, the jet transitions through four dynamical states: limit cycle ![]() $\rightarrow$ quasiperiodicity
$\rightarrow$ quasiperiodicity ![]() $\rightarrow$ intermittency
$\rightarrow$ intermittency ![]() $\rightarrow$ chaos. Next, we give an overview of these four states, before delving into a detailed analysis of the intermittent state in § 3.2.
$\rightarrow$ chaos. Next, we give an overview of these four states, before delving into a detailed analysis of the intermittent state in § 3.2.

Figure 2. Overview of the type-II intermittency route to chaos in a forced globally unstable jet: (a) bifurcation map, (b) time traces of the velocity fluctuation ![]() $u^{\prime }$ with the window
$u^{\prime }$ with the window ![]() $t = 0\unicode{x2013}0.05$ s zoomed in, (c) PSD of
$t = 0\unicode{x2013}0.05$ s zoomed in, (c) PSD of ![]() $u^{\prime }$, (d) phase portraits, and (e) two-sided Poincaré maps. The forcing frequency is fixed at a representative value of
$u^{\prime }$, (d) phase portraits, and (e) two-sided Poincaré maps. The forcing frequency is fixed at a representative value of ![]() $f_f/f_n = 1.78$, while the normalised forcing amplitude
$f_f/f_n = 1.78$, while the normalised forcing amplitude ![]() $\alpha$ is varied (see labels on the far right of (e)). Four dynamical states are highlighted: (
$\alpha$ is varied (see labels on the far right of (e)). Four dynamical states are highlighted: (![]() $\alpha = 0$, green) period-1 limit cycle, (
$\alpha = 0$, green) period-1 limit cycle, (![]() $\alpha = 0.9$, blue)
$\alpha = 0.9$, blue) ![]() $\mathbb {T}^2$ quasiperiodicity, (
$\mathbb {T}^2$ quasiperiodicity, (![]() $\alpha = 1.1$ and
$\alpha = 1.1$ and ![]() $1.3$, red) type-II intermittency and (
$1.3$, red) type-II intermittency and (![]() $\alpha = 1.8$, orange) low-dimensional chaos. In panels (d,e), phase space reconstruction is performed via the embedding theorem of Takens (Reference Takens1981) with a delay time of
$\alpha = 1.8$, orange) low-dimensional chaos. In panels (d,e), phase space reconstruction is performed via the embedding theorem of Takens (Reference Takens1981) with a delay time of ![]() $\tau = 0.52$ ms
$\tau = 0.52$ ms ![]() ${\approx }1/(4f_n)$.
${\approx }1/(4f_n)$.
(i) Limit cycle. When unforced (![]() $\alpha =0$), the jet oscillates in a period-1 limit cycle at the natural frequency of its global mode,
$\alpha =0$), the jet oscillates in a period-1 limit cycle at the natural frequency of its global mode, ![]() $f_n$. This is evidenced by the tight concentration of data points in the bifurcation map (figure 2a), the regularity of the
$f_n$. This is evidenced by the tight concentration of data points in the bifurcation map (figure 2a), the regularity of the ![]() $u^{\prime }$ waveform (figure 2b), the sharp peak at
$u^{\prime }$ waveform (figure 2b), the sharp peak at ![]() $f_n$ in the power spectral density (PSD; figure 2c), the closed orbit in the phase portrait (figure 2d), and the two clusters of intercepts in the two-sided Poincaré map (figure 2e). In figure 2(d,e), phase space reconstruction is performed via the embedding theorem of Takens (Reference Takens1981), with the optimal delay time (
$f_n$ in the power spectral density (PSD; figure 2c), the closed orbit in the phase portrait (figure 2d), and the two clusters of intercepts in the two-sided Poincaré map (figure 2e). In figure 2(d,e), phase space reconstruction is performed via the embedding theorem of Takens (Reference Takens1981), with the optimal delay time (![]() $\tau = 0.52$ ms) found via the first local minimum of the average mutual information function (Fraser & Swinney Reference Fraser and Swinney1986). This delay time maximises the degree of attractor unfolding and corresponds to approximately one-quarter of the oscillation period of the natural global mode,
$\tau = 0.52$ ms) found via the first local minimum of the average mutual information function (Fraser & Swinney Reference Fraser and Swinney1986). This delay time maximises the degree of attractor unfolding and corresponds to approximately one-quarter of the oscillation period of the natural global mode, ![]() $\tau \approx 1/(4f_n)$.
$\tau \approx 1/(4f_n)$.
(ii) Quasiperiodicity. When forced at a low amplitude (![]() $0 < \alpha < 1$), the jet continues to be globally unstable at
$0 < \alpha < 1$), the jet continues to be globally unstable at ![]() $f_n^*$, where the superscript
$f_n^*$, where the superscript ![]() $*$ denotes the presence of forcing. However, the jet also responds at
$*$ denotes the presence of forcing. However, the jet also responds at ![]() $f_f$, which is incommensurable with
$f_f$, which is incommensurable with ![]() $f_n^*$, resulting in a transition to a two-frequency quasiperiodic state characterised by ergodic evolution on a two-dimensional torus attractor
$f_n^*$, resulting in a transition to a two-frequency quasiperiodic state characterised by ergodic evolution on a two-dimensional torus attractor ![]() $\mathbb {T}^2$. This is indicated by the emergence of a toroidal structure in the phase portrait (figure 2d), giving rise to a pair of closed loops in the Poincaré map (figure 2e). It is also indicated by the amplitude modulations in the
$\mathbb {T}^2$. This is indicated by the emergence of a toroidal structure in the phase portrait (figure 2d), giving rise to a pair of closed loops in the Poincaré map (figure 2e). It is also indicated by the amplitude modulations in the ![]() $u^{\prime }$ waveform (figure 2b) and by the coexistence of sharp peaks at both
$u^{\prime }$ waveform (figure 2b) and by the coexistence of sharp peaks at both ![]() $f_n^*$ and
$f_n^*$ and ![]() $f_f$ in the PSD (figure 2c), along with a spectral component at the binaural modulation frequency,
$f_f$ in the PSD (figure 2c), along with a spectral component at the binaural modulation frequency, ![]() $f_1 = f_f - f_n^*$. These observations show that the jet has undergone a Neimark–Sacker bifurcation, transitioning from a period-1 limit cycle to a
$f_1 = f_f - f_n^*$. These observations show that the jet has undergone a Neimark–Sacker bifurcation, transitioning from a period-1 limit cycle to a ![]() $\mathbb {T}^2$ quasiperiodic attractor when forcing is introduced.
$\mathbb {T}^2$ quasiperiodic attractor when forcing is introduced.
(iii) Intermittency. When forced at a higher amplitude (![]() $1 \leq \alpha < 1.74$), the jet remains quasiperiodic for some of the time, but becomes chaotic at other times. This intermittent switching is directly visible in the bifurcation map and the
$1 \leq \alpha < 1.74$), the jet remains quasiperiodic for some of the time, but becomes chaotic at other times. This intermittent switching is directly visible in the bifurcation map and the ![]() $u^{\prime }$ waveform (figure 2a,b), where low-amplitude chaotic epochs appear intermittently amidst a background of mid-amplitude quasiperiodic dynamics. As
$u^{\prime }$ waveform (figure 2a,b), where low-amplitude chaotic epochs appear intermittently amidst a background of mid-amplitude quasiperiodic dynamics. As ![]() $\alpha$ increases, both the lifetime and frequency of the chaotic epochs increase, ultimately yielding sustained chaos. Meanwhile, the PSD shows that the natural mode (
$\alpha$ increases, both the lifetime and frequency of the chaotic epochs increase, ultimately yielding sustained chaos. Meanwhile, the PSD shows that the natural mode ( ![]() $f_n^*$) is gradually pushed away from the forced mode (
$f_n^*$) is gradually pushed away from the forced mode ( ![]() $f_f$), while its tonal nature becomes more broadband; this weakens the binaural effect that initially led to the apparent component at
$f_f$), while its tonal nature becomes more broadband; this weakens the binaural effect that initially led to the apparent component at ![]() $f_1$ (figure 2c). The phase space contains a chaotic saddle at the core and a
$f_1$ (figure 2c). The phase space contains a chaotic saddle at the core and a ![]() $\mathbb {T}^2$ orbit around its periphery (figure 2d,e). In § 3.2, we will examine the reinjection processes that govern how the jet switches between the two saddles.
$\mathbb {T}^2$ orbit around its periphery (figure 2d,e). In § 3.2, we will examine the reinjection processes that govern how the jet switches between the two saddles.
(iv) Chaos. When forced at an even higher amplitude (![]() $1.74 \leq \alpha \leq 2.2$), the jet ceases switching intermittently. Instead, it remains continuously on the chaotic attractor, taking on a low-amplitude state of sustained chaos. This is evidenced by the near-random scattering of data points in the bifurcation map (figure 2a), the irregularity of the
$1.74 \leq \alpha \leq 2.2$), the jet ceases switching intermittently. Instead, it remains continuously on the chaotic attractor, taking on a low-amplitude state of sustained chaos. This is evidenced by the near-random scattering of data points in the bifurcation map (figure 2a), the irregularity of the ![]() $u^{\prime }$ waveform (figure 2b), the broadband spectral features of the PSD (figure 2c), and the intricate structures and trajectory intercepts in the phase space (figure 2d,e).
$u^{\prime }$ waveform (figure 2b), the broadband spectral features of the PSD (figure 2c), and the intricate structures and trajectory intercepts in the phase space (figure 2d,e).
We use schlieren imaging to examine the spatial structure of the global mode, with a view to identifying the origin of the aperiodic dynamics. As figure 3 shows, the jet remains dominated by axisymmetric structures (zero azimuthal wavenumber) for all four dynamical states encountered in this study: limit cycle, quasiperiodicity, intermittency and chaos. The robustness of this axisymmetry suggests that the observed aperiodicity is not due to the excitation of helical modes.

Figure 3. Schlieren snapshots of a globally unstable jet forced at the conditions of figure 2: (a) limit cycle at ![]() $\alpha = 0$, (b) quasiperiodicity at
$\alpha = 0$, (b) quasiperiodicity at ![]() $\alpha = 0.9$, (c,d) intermittency at
$\alpha = 0.9$, (c,d) intermittency at ![]() $\alpha = 1.1$ and
$\alpha = 1.1$ and ![]() $1.3$ and (e) chaos at
$1.3$ and (e) chaos at ![]() $\alpha = 1.8$.
$\alpha = 1.8$.
Next, we apply three more tools from dynamical systems theory to verify the existence of chaos and characterise its fractal properties. For completeness, we also apply the same tools to the limit-cycle attractor (![]() $\alpha =0$) and the
$\alpha =0$) and the ![]() $\mathbb {T}^2$ quasiperiodic attractor (
$\mathbb {T}^2$ quasiperiodic attractor (![]() $\alpha =0.9$).
$\alpha =0.9$).
First, we analyse the topological self-similarity of the attractors by estimating their active degrees of freedom. We do this through the correlation dimension (![]() $\bar {D_c}$), as computed from the
$\bar {D_c}$), as computed from the ![]() $u^{\prime }$ signal via the method of Grassberger & Procaccia (Reference Grassberger and Procaccia1983). We use
$u^{\prime }$ signal via the method of Grassberger & Procaccia (Reference Grassberger and Procaccia1983). We use ![]() $2^{16}$ data points in each computation and round the estimated
$2^{16}$ data points in each computation and round the estimated ![]() $\bar {D_c}$ value to two significant figures, providing sufficient precision to distinguish between fractal and non-fractal behaviour. Figure 4(
$\bar {D_c}$ value to two significant figures, providing sufficient precision to distinguish between fractal and non-fractal behaviour. Figure 4(![]() $a$i,
$a$i,![]() $b$i,
$b$i,![]() $c$i) shows the local gradient of the correlation sum (
$c$i) shows the local gradient of the correlation sum (![]() ${D_c} \equiv \partial \log C_N /\partial \log R$) vs the normalised hypersphere radius (
${D_c} \equiv \partial \log C_N /\partial \log R$) vs the normalised hypersphere radius (![]() $R/R_{max}$) for a delay time of
$R/R_{max}$) for a delay time of ![]() $\tau = 0.52$ ms
$\tau = 0.52$ ms ![]() $\approx 1/(4f_n)$ and an embedding dimension of
$\approx 1/(4f_n)$ and an embedding dimension of ![]() $m = 6,\ 8$ and
$m = 6,\ 8$ and ![]() $10$. Here
$10$. Here ![]() $C_N$ is the correlation sum,
$C_N$ is the correlation sum, ![]() $R$ is the hypersphere radius, and
$R$ is the hypersphere radius, and ![]() $R_{max}$ is its maximum value. For the limit-cycle state (figure 4
$R_{max}$ is its maximum value. For the limit-cycle state (figure 4![]() $a$i),
$a$i), ![]() $D_c$ takes on a mean value of
$D_c$ takes on a mean value of ![]() $\bar {{D_c}} \approx 1.0$ across the self-similar range of Euclidean scales (
$\bar {{D_c}} \approx 1.0$ across the self-similar range of Euclidean scales (![]() $0.06 \leq R/R_{max} \leq 0.5$), confirming that the jet evolves on a closed periodic orbit. For the quasiperiodic state (figure 4
$0.06 \leq R/R_{max} \leq 0.5$), confirming that the jet evolves on a closed periodic orbit. For the quasiperiodic state (figure 4![]() $b$i),
$b$i), ![]() $\bar {{D_c}} \approx 2.0$ across the primary self-similar range (
$\bar {{D_c}} \approx 2.0$ across the primary self-similar range (![]() $0.045 \leq R/R_{max} \leq 0.15$), which is consistent with a
$0.045 \leq R/R_{max} \leq 0.15$), which is consistent with a ![]() $\mathbb {T}^2$ torus attractor with two incommensurable modes. For the chaotic state (figure 4
$\mathbb {T}^2$ torus attractor with two incommensurable modes. For the chaotic state (figure 4![]() $c$i),
$c$i), ![]() $\bar {{D_c}}$ converges to a non-integer value of
$\bar {{D_c}}$ converges to a non-integer value of ![]() $4.5$ across the self-similar range (
$4.5$ across the self-similar range (![]() $0.035 \leq R/R_{max} \leq 0.1$), indicating that this chaotic attractor is both strange and low-dimensional (Ott Reference Ott2002).
$0.035 \leq R/R_{max} \leq 0.1$), indicating that this chaotic attractor is both strange and low-dimensional (Ott Reference Ott2002).

Figure 4. Evidence of low-dimensional chaos on a strange attractor: (![]() $a$i–
$a$i–![]() $c$i) the correlation-sum gradient vs the normalised hypersphere radius, (
$c$i) the correlation-sum gradient vs the normalised hypersphere radius, (![]() $a$ii–
$a$ii–![]() $c$ii) the translation components, mean squared displacement and asymptotic growth rate K from the 0–1 test, and (
$c$ii) the translation components, mean squared displacement and asymptotic growth rate K from the 0–1 test, and (![]() $a$iii–
$a$iii–![]() $c$iii) the mean degree of the filtered horizontal visibility graph vs the amplitude of the noise filter. The mean degree at a noise-filter amplitude of
$c$iii) the mean degree of the filtered horizontal visibility graph vs the amplitude of the noise filter. The mean degree at a noise-filter amplitude of ![]() $\beta = 0.08$ is denoted as
$\beta = 0.08$ is denoted as ![]() $\bar {k}_{0.08}$. Three dynamical states from figure 2 are shown: (
$\bar {k}_{0.08}$. Three dynamical states from figure 2 are shown: (![]() $a$: green) period-1 limit cycle at
$a$: green) period-1 limit cycle at ![]() $\alpha = 0$, (
$\alpha = 0$, (![]() $b$: blue)
$b$: blue) ![]() $\mathbb {T}^2$ quasiperiodicity at
$\mathbb {T}^2$ quasiperiodicity at ![]() $\alpha = 0.9$, and (
$\alpha = 0.9$, and (![]() $c$: orange) low-dimensional chaos at
$c$: orange) low-dimensional chaos at ![]() $\alpha = 1.8$.
$\alpha = 1.8$.
Second, we confirm the presence of deterministic chaos by applying the 0–1 test of Gottwald & Melbourne (Reference Gottwald and Melbourne2004). For both the limit-cycle state (figure 4![]() $a$ii) and the quasiperiodic state (figure 4
$a$ii) and the quasiperiodic state (figure 4![]() $b$ii), the translation components [
$b$ii), the translation components [![]() $p(n)$,
$p(n)$, ![]() $q(n)$ with
$q(n)$ with ![]() $n=1,2,\ldots,N$] form a circular pattern, with the mean squared displacement
$n=1,2,\ldots,N$] form a circular pattern, with the mean squared displacement ![]() $M(n)$ remaining bounded in time, resulting in a median growth rate of
$M(n)$ remaining bounded in time, resulting in a median growth rate of ![]() $K_m \approx 0$. These translation features indicate non-chaotic dynamics (Gottwald & Melbourne Reference Gottwald and Melbourne2004). For the chaotic state (figure 4
$K_m \approx 0$. These translation features indicate non-chaotic dynamics (Gottwald & Melbourne Reference Gottwald and Melbourne2004). For the chaotic state (figure 4![]() $c$ii), the translation components form a Brownian-like pattern, with
$c$ii), the translation components form a Brownian-like pattern, with ![]() $M(n)$ increasing linearly in time at a median rate of
$M(n)$ increasing linearly in time at a median rate of ![]() $K_m \approx 1$. These translation features indicate chaotic dynamics, which is consistent with the non-integer value of
$K_m \approx 1$. These translation features indicate chaotic dynamics, which is consistent with the non-integer value of ![]() $\bar {D_c}$ found above and with our initial assessment of figure 2.
$\bar {D_c}$ found above and with our initial assessment of figure 2.
Third, we further confirm the presence of deterministic chaos by transforming the ![]() $u^{\prime }$ signal into complex networks using the filtered horizontal visibility graph of Nuñez et al. (Reference Nuñez, Lacasa, Valero, Gómez and Luque2012). This tool can identify periodic structures concealed within noise-corrupted signals, allowing for the differentiation of chaotic, stochastic and noisy periodic dynamics. For both the limit-cycle state (figure 4
$u^{\prime }$ signal into complex networks using the filtered horizontal visibility graph of Nuñez et al. (Reference Nuñez, Lacasa, Valero, Gómez and Luque2012). This tool can identify periodic structures concealed within noise-corrupted signals, allowing for the differentiation of chaotic, stochastic and noisy periodic dynamics. For both the limit-cycle state (figure 4![]() $a$iii) and the quasiperiodic state (figure 4
$a$iii) and the quasiperiodic state (figure 4![]() $b$iii), the mean degree
$b$iii), the mean degree ![]() $\bar {k}$ falls to exactly 2 as the amplitude of the graph–theoretical noise filter increases to a high value (
$\bar {k}$ falls to exactly 2 as the amplitude of the graph–theoretical noise filter increases to a high value (![]() $\beta = 0.08$). This indicates that both states are dominated by regular dynamics of temporal period
$\beta = 0.08$). This indicates that both states are dominated by regular dynamics of temporal period ![]() $\mathcal {T}=1$, which is consistent with the prevailing strength of the
$\mathcal {T}=1$, which is consistent with the prevailing strength of the ![]() $f_n$ mode in the limit-cycle case and that of the
$f_n$ mode in the limit-cycle case and that of the ![]() $f_n^*$ mode in the quasiperiodic case (see the PSD in figure 2
$f_n^*$ mode in the quasiperiodic case (see the PSD in figure 2![]() $c$). In the quasiperiodic case, there are also spectral components at
$c$). In the quasiperiodic case, there are also spectral components at ![]() $f_f$ and
$f_f$ and ![]() $f_1$, but these are significantly weaker than the natural hydrodynamic mode at
$f_1$, but these are significantly weaker than the natural hydrodynamic mode at ![]() $f_n^*$, leaving the system to be dominated by the latter. For the chaotic state (figure 4
$f_n^*$, leaving the system to be dominated by the latter. For the chaotic state (figure 4![]() $c$iii),
$c$iii), ![]() $\bar {k}$ fails to converge even at a high value of
$\bar {k}$ fails to converge even at a high value of ![]() $\beta$, indicating the absence of any periodic structure in the signal. When combined with the limited degrees of freedom (
$\beta$, indicating the absence of any periodic structure in the signal. When combined with the limited degrees of freedom (![]() $\bar {D_c} \approx 4.5$), this confirms that this state is governed by chaotic processes, rather than by stochastic processes embedded in a periodic signal.
$\bar {D_c} \approx 4.5$), this confirms that this state is governed by chaotic processes, rather than by stochastic processes embedded in a periodic signal.
In summary, by applying the correlation dimension, the 0–1 test and the filtered horizontal visibility graph, we have found definitive evidence that a forced globally unstable jet can exhibit low-dimensional deterministic chaos on a strange attractor.
3.2. Identification of the intermittency type
We conduct a detailed analysis of the intermittent state (![]() $1 \leq \alpha < 1.74$) to identify the route to chaos. Figure 5(
$1 \leq \alpha < 1.74$) to identify the route to chaos. Figure 5(![]() $a$i) shows a partial segment of the full 60 s time series of the normalised velocity fluctuation,
$a$i) shows a partial segment of the full 60 s time series of the normalised velocity fluctuation, ![]() $\tilde {u}^\prime (t) \equiv u^\prime (t)/u^\prime _{max}$, where
$\tilde {u}^\prime (t) \equiv u^\prime (t)/u^\prime _{max}$, where ![]() $u'_{max}$ is the maximum velocity fluctuation. We observe intermittent switching between mid-amplitude quasiperiodic epochs (figure 5
$u'_{max}$ is the maximum velocity fluctuation. We observe intermittent switching between mid-amplitude quasiperiodic epochs (figure 5![]() $a$ii) and low-amplitude chaotic epochs (figure 5
$a$ii) and low-amplitude chaotic epochs (figure 5![]() $a$iv) via a transition regime (figure 5
$a$iv) via a transition regime (figure 5![]() $a$iii). We use two methods to identify the intermittency type.
$a$iii). We use two methods to identify the intermittency type.

Figure 5. Evidence of type-II intermittency: (a) time traces of ![]() $\tilde {u}^\prime$ showing irregular switching between quasiperiodicity and chaos, (b) the average inter-chaos time
$\tilde {u}^\prime$ showing irregular switching between quasiperiodicity and chaos, (b) the average inter-chaos time ![]() $\bar {T}$ vs the control parameter
$\bar {T}$ vs the control parameter ![]() $\epsilon \equiv \alpha - 1$, and (c) the first return map of successive local maxima. In panels (a) and (c), the forcing amplitude is
$\epsilon \equiv \alpha - 1$, and (c) the first return map of successive local maxima. In panels (a) and (c), the forcing amplitude is ![]() $\alpha =1.1$ (
$\alpha =1.1$ (![]() $\epsilon = 0.1$).
$\epsilon = 0.1$).
First, we compile statistics on the lifetime (![]() $T$) of every quasiperiodic epoch (i.e. the regular phase) using a velocity amplitude threshold of
$T$) of every quasiperiodic epoch (i.e. the regular phase) using a velocity amplitude threshold of ![]() $\tilde {u}^\prime = 0.43$, as indicated by the horizontal dashed line in figure 5(
$\tilde {u}^\prime = 0.43$, as indicated by the horizontal dashed line in figure 5(![]() $a$i);
$a$i); ![]() $T$ is also known as the inter-chaos time. We use this threshold value as it provides a robust balance between rejecting the chaotic epochs and capturing the quasiperiodic epochs. A sensitivity analysis of the scaling properties of
$T$ is also known as the inter-chaos time. We use this threshold value as it provides a robust balance between rejecting the chaotic epochs and capturing the quasiperiodic epochs. A sensitivity analysis of the scaling properties of ![]() $T$ reveals no significant variation within a threshold range of
$T$ reveals no significant variation within a threshold range of ![]() $\tilde {u}^\prime \in [0.40, 0.45]$. Figure 5(b) shows on double-logarithmic axes the average value of
$\tilde {u}^\prime \in [0.40, 0.45]$. Figure 5(b) shows on double-logarithmic axes the average value of ![]() $T$, or
$T$, or ![]() $\bar {T}$, as a function of the proximity to the critical forcing amplitude at the onset of intermittency,
$\bar {T}$, as a function of the proximity to the critical forcing amplitude at the onset of intermittency, ![]() $\epsilon \equiv \alpha - 1$. We find that
$\epsilon \equiv \alpha - 1$. We find that ![]() $\bar {T}$ decreases as
$\bar {T}$ decreases as ![]() $\epsilon$ increases, indicating that the quasiperiodic dynamics is gradually replaced by chaotic dynamics as the forcing strengthens. The gradual nature of this replacement process is characteristic of the intermittency route to chaos (Ott Reference Ott2002; Schuster & Just Reference Schuster and Just2005). Crucially, we find an inverse power-law relationship of the form
$\epsilon$ increases, indicating that the quasiperiodic dynamics is gradually replaced by chaotic dynamics as the forcing strengthens. The gradual nature of this replacement process is characteristic of the intermittency route to chaos (Ott Reference Ott2002; Schuster & Just Reference Schuster and Just2005). Crucially, we find an inverse power-law relationship of the form ![]() $\bar {T} \sim \epsilon ^{-1.01}$, where the exponent has a 95 % confidence limit of
$\bar {T} \sim \epsilon ^{-1.01}$, where the exponent has a 95 % confidence limit of ![]() $\pm 0.15$. According to the reinjection theory of Pomeau & Manneville (Reference Pomeau and Manneville1980), the power-law exponent is expected to be
$\pm 0.15$. According to the reinjection theory of Pomeau & Manneville (Reference Pomeau and Manneville1980), the power-law exponent is expected to be ![]() $-1$ for type-II or type-III intermittency, but
$-1$ for type-II or type-III intermittency, but ![]() $-1/2$ for type-I intermittency. Therefore, the power-law exponent of
$-1/2$ for type-I intermittency. Therefore, the power-law exponent of ![]() $-1.01$ observed in figure 5(b) rules out the possibility of type-I intermittency in our system.
$-1.01$ observed in figure 5(b) rules out the possibility of type-I intermittency in our system.
Second, we plot in figure 5(c) an array of successive local maxima ![]() $\tilde {u}^\prime _{max}(i)$ extracted from the regular phase (quasiperiodicity) along with a copy of itself shifted by one sample index
$\tilde {u}^\prime _{max}(i)$ extracted from the regular phase (quasiperiodicity) along with a copy of itself shifted by one sample index ![]() $\tilde {u}^\prime _{max}(i+1)$. This is known as the first return map, whose features can reveal the intermittency type (Ott Reference Ott2002). Previous studies have established that the data points in the first return map pass through a tunnel next to the main diagonal for type-I intermittency (Schuster & Just Reference Schuster and Just2005), they form a spiral pattern for type-II intermittency (Arneodo, Coullet & Tresser Reference Arneodo, Coullet and Tresser1981; Sacher, Elsässer & Göbel Reference Sacher, Elsässer and Göbel1989; Ganapathy & Sood Reference Ganapathy and Sood2006), and they cross the main diagonal along a tangent-function-like path for type-III intermittency (Griffith et al. Reference Griffith, Parthimos, Crombie and Edwards1997). In figure 5(c), the data points form a clear spiral pattern, confirming that the intermittency in our system is of type II.
$\tilde {u}^\prime _{max}(i+1)$. This is known as the first return map, whose features can reveal the intermittency type (Ott Reference Ott2002). Previous studies have established that the data points in the first return map pass through a tunnel next to the main diagonal for type-I intermittency (Schuster & Just Reference Schuster and Just2005), they form a spiral pattern for type-II intermittency (Arneodo, Coullet & Tresser Reference Arneodo, Coullet and Tresser1981; Sacher, Elsässer & Göbel Reference Sacher, Elsässer and Göbel1989; Ganapathy & Sood Reference Ganapathy and Sood2006), and they cross the main diagonal along a tangent-function-like path for type-III intermittency (Griffith et al. Reference Griffith, Parthimos, Crombie and Edwards1997). In figure 5(c), the data points form a clear spiral pattern, confirming that the intermittency in our system is of type II.
In summary, by analysing the scaling behaviour of the average inter-chaos time and the first return map, we have determined that the intermittency observed en route to chaos in our jet conforms to type II of the Pomeau & Manneville (Reference Pomeau and Manneville1980) classification.
4. Conclusions and discussion
Previous reports of chaos in open-jet flows have been limited to globally stable jets dominated by local convective instability. In this experimental study, we have provided the first conclusive evidence of chaos in a globally unstable jet: an axisymmetric inertial low-density jet containing a large enough region of local absolute instability to support a hydrodynamically self-excited global mode. We found that when forced externally with an increasing amplitude at an off-resonant frequency ( ![]() $f_f/f_n \in [1.75, 1.81]$), the jet exhibits a sequence of nonlinear states: period-1 limit cycle
$f_f/f_n \in [1.75, 1.81]$), the jet exhibits a sequence of nonlinear states: period-1 limit cycle ![]() $\rightarrow$ quasiperiodicity on a
$\rightarrow$ quasiperiodicity on a ![]() $\mathbb {T}^2$ torus attractor
$\mathbb {T}^2$ torus attractor ![]() $\rightarrow$ type-II intermittency of the Pomeau & Manneville (Reference Pomeau and Manneville1980) class
$\rightarrow$ type-II intermittency of the Pomeau & Manneville (Reference Pomeau and Manneville1980) class ![]() $\rightarrow$ low-dimensional chaos on a strange attractor. We verified the low-dimensional fractal nature of the chaotic state through (i) the correlation dimension converging to a non-integer value of
$\rightarrow$ low-dimensional chaos on a strange attractor. We verified the low-dimensional fractal nature of the chaotic state through (i) the correlation dimension converging to a non-integer value of ![]() $\bar {{D_c}} \approx 4.5$, (ii) the 0–1 test returning Brownian-like translation patterns and a growth rate of the mean squared displacement of
$\bar {{D_c}} \approx 4.5$, (ii) the 0–1 test returning Brownian-like translation patterns and a growth rate of the mean squared displacement of ![]() $K_m \approx 1$, and (iii) the filtered horizontal visibility graph exhibiting a non-converging mean degree. The intermittent state features switching between mid-amplitude quasiperiodic epochs and low-amplitude chaotic epochs. We verified the type-II nature of this state through (i) the power-law relationship between the average inter-chaos time
$K_m \approx 1$, and (iii) the filtered horizontal visibility graph exhibiting a non-converging mean degree. The intermittent state features switching between mid-amplitude quasiperiodic epochs and low-amplitude chaotic epochs. We verified the type-II nature of this state through (i) the power-law relationship between the average inter-chaos time ![]() $\bar {T}$ and the control parameter
$\bar {T}$ and the control parameter ![]() $\epsilon$, with a scaling exponent approaching the theoretical value of
$\epsilon$, with a scaling exponent approaching the theoretical value of ![]() $-1$, and (ii) the first return map showing a clear spiral pattern. When considered together, these observations offer compelling evidence that the globally unstable jet has transitioned into a state of low-dimensional chaos on a strange attractor via type-II intermittency conforming to the class of Pomeau & Manneville (Reference Pomeau and Manneville1980).
$-1$, and (ii) the first return map showing a clear spiral pattern. When considered together, these observations offer compelling evidence that the globally unstable jet has transitioned into a state of low-dimensional chaos on a strange attractor via type-II intermittency conforming to the class of Pomeau & Manneville (Reference Pomeau and Manneville1980).
The discovery of the type-II intermittency route to chaos in a forced globally unstable jet has several implications. First, it strengthens the argument that strange attractors emerge via universal mechanisms in open self-excited flows (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Manneville Reference Manneville2010). This could accelerate the development of instability control strategies for such flows by leveraging both emerging and established actuation concepts from chaos theory (Boccaletti et al. Reference Boccaletti, Grebogi, Lai, Mancini and Maza2000). Second, the type-II intermittency route to chaos has also been observed in various other dynamical systems in nature and engineering, and can be readily modelled (Ott Reference Ott2002; Schuster & Just Reference Schuster and Just2005). This suggests that it might be possible to build on those existing modelling efforts to better understand and predict the stability and dynamics of open self-excited flows, especially their transition from a regular state to a chaotic state en route to turbulence. Third, the presence of chaos in an open self-excited flow can be detrimental in situations where the flow interacts with a deformable structure or an acoustic field. This is because such chaotic flow oscillations would generate broadband spectral components with the potential to readily excite resonant modes in the structure or acoustic field. Encouragingly, the presence of intermittency preceding chaos in the present flow suggests that it might be possible to detect precursors of chaos using proven tools such as complex networks, multifractal analysis, and recurrence quantification analysis (Sujith & Unni Reference Sujith and Unni2020). Fourth, our findings reveal that even when subjected to strong periodic forcing, a globally unstable jet may not necessarily synchronise with that forcing. Instead, it can exhibit far more complex dynamics, such as intermittency and strange chaotic attractors. In the field of nonlinear dynamics, the breakdown of a ![]() $\mathbb {T}^2$ torus into chaos due to strong external forcing has been analysed by Aronson et al. (Reference Aronson, Chory, Hall and McGehee1982) using a family of maps, with Afraimovich & Shilnikov (Reference Afraimovich and Shilnikov1991) focusing on the specific case of a phase-locked torus. Intermittency can occur in two of the main breakdown scenarios, one involving the birth of a homoclinic orbit and the other involving the formation of a non-smooth manifold homeomorphic to the torus (Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2003). Both scenarios are found only near the outer regions of the Arnold tongue, which may explain why we observe intermittency at a relatively large detuning. It is worth noting that our full experimental campaign covers a wide range of forcing frequencies (
$\mathbb {T}^2$ torus into chaos due to strong external forcing has been analysed by Aronson et al. (Reference Aronson, Chory, Hall and McGehee1982) using a family of maps, with Afraimovich & Shilnikov (Reference Afraimovich and Shilnikov1991) focusing on the specific case of a phase-locked torus. Intermittency can occur in two of the main breakdown scenarios, one involving the birth of a homoclinic orbit and the other involving the formation of a non-smooth manifold homeomorphic to the torus (Pikovsky, Rosenblum & Kurths Reference Pikovsky, Rosenblum and Kurths2003). Both scenarios are found only near the outer regions of the Arnold tongue, which may explain why we observe intermittency at a relatively large detuning. It is worth noting that our full experimental campaign covers a wide range of forcing frequencies ( ![]() $f_f/f_n \in [0.30, 2.10]$), enabling synchronisation to be detected in the 2:1, 1:1 and 1:2 Arnold tongues. Between the 1:1 and 1:2 tongues, we find the classic Ruelle–Takens–Newhouse route to chaos, along which the dressed winding number (
$f_f/f_n \in [0.30, 2.10]$), enabling synchronisation to be detected in the 2:1, 1:1 and 1:2 Arnold tongues. Between the 1:1 and 1:2 tongues, we find the classic Ruelle–Takens–Newhouse route to chaos, along which the dressed winding number ( ![]() $f_n^*/f_f$) approaches the golden mean (
$f_n^*/f_f$) approaches the golden mean (![]() $\sigma _g = (\sqrt {5}-1)/2$) and the distribution of spectral peaks aligns with the Fibonacci sequence. Thus, for certain forcing conditions at the onset of chaos, the jet obeys the universal scaling properties of the sine circle map (Olinger & Sreenivasan Reference Olinger and Sreenivasan1988; Ott Reference Ott2002). We also find the period-doubling route to chaos around the 2:1 tongue, as well as strange non-chaotic attractors and crisis-induced intermittency around the 1:2 tongue. Currently, we are conducting a detailed analysis of these different transition scenarios to better understand the complex jet dynamics. This complexity underscores the importance of exercising caution when selecting the forcing parameters for the open-loop control of globally unstable jets.
$\sigma _g = (\sqrt {5}-1)/2$) and the distribution of spectral peaks aligns with the Fibonacci sequence. Thus, for certain forcing conditions at the onset of chaos, the jet obeys the universal scaling properties of the sine circle map (Olinger & Sreenivasan Reference Olinger and Sreenivasan1988; Ott Reference Ott2002). We also find the period-doubling route to chaos around the 2:1 tongue, as well as strange non-chaotic attractors and crisis-induced intermittency around the 1:2 tongue. Currently, we are conducting a detailed analysis of these different transition scenarios to better understand the complex jet dynamics. This complexity underscores the importance of exercising caution when selecting the forcing parameters for the open-loop control of globally unstable jets.
Acknowledgements
We would like to thank Yuanhang Zhu, Vikrant Gupta and Kelvin Leung for fruitful discussions.
Funding
This work was funded by the Research Grants Council of Hong Kong (project nos. 16210419 and 16200220).
Declaration of interests
The authors report no conflict of interest.