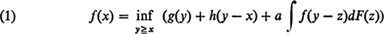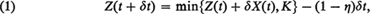Short Communications
Sums of Lifetimes in Age Dependent Branching Processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 195-200
-
- Article
- Export citation
Research Papers
Negative binomial processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 633-647
-
- Article
- Export citation
Integral representations of transition probabilities and serial covariances of certain markov chains
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 648-659
-
- Article
- Export citation
The minimum of a stationary Markov process superimposed on a U-shaped trend
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 399-408
-
- Article
- Export citation
Short Communications
Bounds for Certain Branching Processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 201-204
-
- Article
- Export citation
An Age-Dependent Branching Process with Correlations Among Sister Cells
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 205-210
-
- Article
- Export citation
Research Papers
A characterization of stable processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-418
-
- Article
- Export citation
Random secants of a convex body
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 660-672
-
- Article
- Export citation
Short Communications
Stability Theorems for Solutions to the Optimal Inventory Equation
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 211-217
-
- Article
- Export citation
Research Papers
On the maximum of sums of random variables and the supremum functional for stable processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 419-429
-
- Article
- Export citation
A recursion theorem on solving differential-difference equations and applications to some stochastic processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 673-681
-
- Article
- Export citation
Short Communications
The total progeny in a branching process and a related random walk
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 682-686
-
- Article
- Export citation
Sufficient Conditions for a First Passage Time Process to be that of Brownian Motion
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 218-223
-
- Article
- Export citation
Research Papers
Random paths through convex bodies
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 430-441
-
- Article
- Export citation
Short Communications
The joint asymptotic distribution of the k-smallest sample spacings
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 442-448
-
- Article
- Export citation
A Note on Absorption Probabilities for a Random Walk Between a Reflecting and an Absorbing Barrier
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 224-226
-
- Article
- Export citation
A birth, death and migration process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 687-691
-
- Article
- Export citation
Optimal dispatching of a poisson process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 692-699
-
- Article
- Export citation
A Note on the First Emptiness Problem of a Finite Dam with Poisson Type Inputs
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 227-230
-
- Article
- Export citation
A note on stochastic processes with independent increments taking values in an abelian group
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 449-452
-
- Article
- Export citation