Research Papers
Extended criterion for comparison of empirical distributions
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-20
-
- Article
- Export citation
A generalized unimodality
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 21-34
-
- Article
- Export citation
Sur L'enveloppe convexe des nuages de points aleatoires dans Rn. I
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 35-48
-
- Article
- Export citation
Solutions of ordinary differential equations as limits of pure jump markov processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 49-58
-
- Article
- Export citation
On Wald's equations in continuous time
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 59-68
-
- Article
- Export citation
A stochastic process related to language change
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 69-78
-
- Article
- Export citation
The recovery of the root of a tree
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 79-88
-
- Article
- Export citation
Maximal branching processes and ‘long-range percolation’
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 89-98
-
- Article
- Export citation
Extreme value theory for a class of discrete distributions with applications to some stochastic processes
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 99-113
-
- Article
- Export citation
On the fluctuations of election returns
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-123
-
- Article
- Export citation
On a generalized entropy and a coding theorem
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 124-133
-
- Article
- Export citation
Optimal reinsurance
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 134-156
-
- Article
- Export citation
On some problems in operations research
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 157-164
-
- Article
- Export citation
Mean life of series and parallel systems
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 165-174
-
- Article
- Export citation
Bunching in a semi-Markov process
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 175-182
-
- Article
- Export citation
Random displacements of regularly spaced events
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 183-195
-
- Article
- Export citation
Queueing with alternating priorities, treated as random walk on the lattice in the plane
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 196-218
-
- Article
- Export citation
Two results in the theory of queues
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 219-226
-
- Article
- Export citation
Limit theorems for the single server queue with traffic intensity one
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 227-233
-
- Article
- Export citation
Short Communications
Inflow-Stock-Outflow time series, stochastic lag and disaggregation: a note
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 234-239
-
- Article
- Export citation

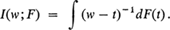
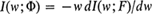 . The equivalence of Khintchine's and Isii's results is made vivid by a proof (due to L. A. Shepp) in the next section.
. The equivalence of Khintchine's and Isii's results is made vivid by a proof (due to L. A. Shepp) in the next section.
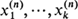 are independent random variables representing their respective numbers of offspring, then the (
are independent random variables representing their respective numbers of offspring, then the (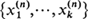 individuals rather than
individuals rather than 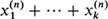 as in the branching case. Equivalently, the transition matrices
as in the branching case. Equivalently, the transition matrices 
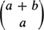 voting records are equally probable. Denote by
voting records are equally probable. Denote by 
 and logarithms will be taken to the base
and logarithms will be taken to the base