Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T05:33:34.386Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fluctuations of election returns

Published online by Cambridge University Press:  14 July 2016

Lajos Takács
Lajos Takács*
Affiliation:
Case Western Reserve University, Cleveland
Get access Rights & Permissions [Opens in a new window]

Extract

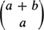Suppose that in a ballot candidate A scores a votes and candidate B scores b votes and all the possible voting records are equally probable. Denote by αr and βr the number of votes registered for A and B respectively among the first r votes counted. For j= 0, 1,···, a + b define Pj(a, b) as the probability that the inequality αr > aβr/b holds for exactly j subscripts r = 1, 2, .., a + b.

Type
Research Papers
Information
Journal of Applied Probability , Volume 7 , Issue 1 , April 1970 , pp. 114 - 123
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Andersen, E. S. (1953) On sums of symmetrically dependent random variables. Skand. Aktuartidskr. 36, 123–138.Google Scholar
[2] Bizley, M. T. L. (1954) Derivation of a new formula for the number of minimal lattice paths from (0,0) to (km, kn) having just t contacts with the line my = nx and having no points above this line; and a proof of Grossman's formula for the number of paths which may touch but do not rise above this line. J. Inst. Actuar. 80, 55–62.CrossRefGoogle Scholar
[3] Bizley, M. T. L. (1967) Problem 5503. Amer. Math. Monthly 74, 728.Google Scholar
[4] Engelberg, O. (1964) Exact and limiting distributions of the number of lead positions in “unconditional” ballot problems. J. Appl. Prob. 1, 168–172.Google Scholar
[5] Feller, W. (1959) On combinatorial methods in fluctuation theory. Probability and Statistics. The Harald Cramer Volume. Ed. Grenander, U.. Almqvist and Wiksell, Stockholm, and J. Wiley and Sons, New York, 75–91.Google Scholar
[6] Grossman, H. D. (1950) Paths in a lattice triangle. Scripta Math. 16, 207–212.Google Scholar
[7] Grossman, H. D. (1954) Paths having a given number of lattice points in a given region. Scripta Math. 20, 203–204.Google Scholar
[8] Hardy, G. H. (1949) Divergent Series. Oxford University Press, Oxford.Google Scholar
[9] Hardy, G. H. and Littlewood, J. E. (1914) Tauberian theorems concerning power series and Dirichlet's series whose coefficients are positive. Proc. Lond. Math. Soc. 13, 174–191.Google Scholar
[10] PóLya, G. and Szegö, G. (1925) Aufgaben und Lehrsätze aus der Analysis. Ed. I. Springer, Berlin.Google Scholar
[11] Takács, L. (1962) Ballot problems. Z. Wahrscheinlichkeitsth. 1, 154–158.Google Scholar
[12] Takács, L. (1964) Fluctuations in the ratio of scores in counting a ballot. J. Appl. Prob. 1, 393–396.Google Scholar
[13] Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. J. Wiley and Sons, New York.Google Scholar
[14] Takács, L. (1969) Solution of Problem 5503. Amer. Math. Monthly (to appear).Google Scholar