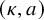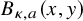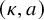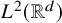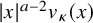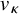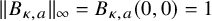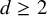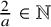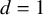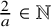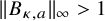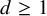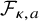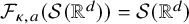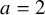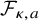1 Introduction
Let as usual
![]() $\Delta $
be the Laplacian operator in
$\Delta $
be the Laplacian operator in
![]() $\mathbb {R}^{d}$
. For the Fourier transform
$\mathbb {R}^{d}$
. For the Fourier transform
Howe [Reference Howe16] obtained the following spectral decomposition of
![]() $\mathcal {F}$
using the harmonic oscillator
$\mathcal {F}$
using the harmonic oscillator
![]() $-({\Delta -|x|^2})/2$
and its eigenfunctions forming the basis in
$-({\Delta -|x|^2})/2$
and its eigenfunctions forming the basis in
![]() $L^{2}(\mathbb {R}^{d})$
:
$L^{2}(\mathbb {R}^{d})$
:
Among other applications, this decomposition is useful to define the fractional power of the Fourier transform (see [Reference Ben Saïd, Kobayashi and Ørsted4, Reference Kobayashi and Mano19]).
During the last 30 years, a lot of attention has been given to various generalizations of the Fourier transform. As an important example, to develop harmonic analysis on weighted spaces, the Dunkl transform was introduced in [Reference Dunkl12]. The Dunkl transform
![]() $\mathcal {F}_\kappa $
is defined with the help of a root system
$\mathcal {F}_\kappa $
is defined with the help of a root system
![]() $\Omega \subset \mathbb {R}^{d}$
, a reflection group
$\Omega \subset \mathbb {R}^{d}$
, a reflection group
![]() $G\subset O(d)$
, and multiplicity function
$G\subset O(d)$
, and multiplicity function
![]() $\kappa \colon \Omega \to \mathbb {R}_+$
, such that
$\kappa \colon \Omega \to \mathbb {R}_+$
, such that
![]() $\kappa $
is G-invariant. Here, G is generated by reflections
$\kappa $
is G-invariant. Here, G is generated by reflections
![]() $\{\sigma _{\alpha }\colon \alpha \in \Omega \}$
, where
$\{\sigma _{\alpha }\colon \alpha \in \Omega \}$
, where
![]() $\sigma _{\alpha }$
is a reflection with respect to hyperplane
$\sigma _{\alpha }$
is a reflection with respect to hyperplane
![]() $(\alpha ,x)=0$
.
$(\alpha ,x)=0$
.
The differential-difference Dunkl Laplacian operator
![]() $\Delta _{\kappa }$
plays the role of the classical Laplacian [Reference Rösler20]. If
$\Delta _{\kappa }$
plays the role of the classical Laplacian [Reference Rösler20]. If
![]() $\kappa \equiv 0$
, we have
$\kappa \equiv 0$
, we have
![]() $\Delta _{\kappa }=\Delta $
. Dunkl Laplacian allows us to define the Dunkl harmonic oscillator
$\Delta _{\kappa }=\Delta $
. Dunkl Laplacian allows us to define the Dunkl harmonic oscillator
![]() $\Delta _{\kappa }-|x|^{2}$
and the Dunkl transform
$\Delta _{\kappa }-|x|^{2}$
and the Dunkl transform
where
 $$\begin{align*}\langle \kappa\rangle=\frac{1}{2}\sum_{\alpha\in \Omega}\kappa(\alpha). \end{align*}$$
$$\begin{align*}\langle \kappa\rangle=\frac{1}{2}\sum_{\alpha\in \Omega}\kappa(\alpha). \end{align*}$$
Further extensions of Fourier and Dunkl transforms were obtained by Ben Saïd, Kobayashi, and Ørsted in [Reference Ben Saïd, Kobayashi and Ørsted4]. They defined the a-deformed Dunkl harmonic oscillator
and the
![]() $(\kappa ,a)$
-generalized Fourier transform
$(\kappa ,a)$
-generalized Fourier transform
which is a two-parameter family of unitary operators in
![]() $L^{2}(\mathbb {R}^{d},d\mu _{\kappa ,a})$
equipped with the norm
$L^{2}(\mathbb {R}^{d},d\mu _{\kappa ,a})$
equipped with the norm
Here
 $$\begin{align*}v_{\kappa}(x)=\prod_{\alpha\in \Omega}|\langle\alpha,x\rangle|^{\kappa(\alpha)},\quad c^{-1}_{\kappa,a}=\int_{\mathbb{R}^{d}}e^{-|x|^{a}/a}v_{\kappa,a}(x)\,dx. \end{align*}$$
$$\begin{align*}v_{\kappa}(x)=\prod_{\alpha\in \Omega}|\langle\alpha,x\rangle|^{\kappa(\alpha)},\quad c^{-1}_{\kappa,a}=\int_{\mathbb{R}^{d}}e^{-|x|^{a}/a}v_{\kappa,a}(x)\,dx. \end{align*}$$
Throughout the paper, we assume that
![]() $ d+2\langle \kappa \rangle +a-2=2\lambda _{\kappa }+a>0$
or, equivalently,
$ d+2\langle \kappa \rangle +a-2=2\lambda _{\kappa }+a>0$
or, equivalently,
![]() $\lambda _{\kappa , a}>-1$
. Note that under this condition, the weight function
$\lambda _{\kappa , a}>-1$
. Note that under this condition, the weight function
![]() $v_{\kappa ,a}$
is locally integrable.
$v_{\kappa ,a}$
is locally integrable.
For
![]() $a=2$
, (1.1) reduces to the Dunkl transform, while if
$a=2$
, (1.1) reduces to the Dunkl transform, while if
![]() $a=2$
and
$a=2$
and
![]() $\kappa \equiv 0$
, then (1.1) is the classical Fourier transform. For
$\kappa \equiv 0$
, then (1.1) is the classical Fourier transform. For
![]() $a\ne 2$
, we arrive at deformed Dunkl and Fourier transforms, which have various applications. In particular, for
$a\ne 2$
, we arrive at deformed Dunkl and Fourier transforms, which have various applications. In particular, for
![]() $a=1$
and
$a=1$
and
![]() $\kappa \equiv 0$
, the deformed Dunkl transform is the unitary inversion operator of the Schrödinger model of minimal representation of the group
$\kappa \equiv 0$
, the deformed Dunkl transform is the unitary inversion operator of the Schrödinger model of minimal representation of the group
![]() $O(N+1,2)$
[Reference Kobayashi and Mano19].
$O(N+1,2)$
[Reference Kobayashi and Mano19].
The unitary operator
![]() $\mathcal {F}_{\kappa ,a}$
on
$\mathcal {F}_{\kappa ,a}$
on
![]() $L^{2}(\mathbb {R}^{d},d\mu _{\kappa ,a})$
can be written as the integral transform [Reference Ben Saïd, Kobayashi and Ørsted4, (5.8)]
$L^{2}(\mathbb {R}^{d},d\mu _{\kappa ,a})$
can be written as the integral transform [Reference Ben Saïd, Kobayashi and Ørsted4, (5.8)]
with the continuous symmetric kernel
![]() $B_{\kappa ,a}(x,y)$
satisfying
$B_{\kappa ,a}(x,y)$
satisfying
![]() $B_{\kappa ,a}(0,y)=1$
. In particular,
$B_{\kappa ,a}(0,y)=1$
. In particular,
![]() $B_{0,2}(x,y)=e^{-i\langle x,y\rangle }$
. One of the fundamental questions in the theory of deformed transforms is to investigate basic properties of the kernel
$B_{0,2}(x,y)=e^{-i\langle x,y\rangle }$
. One of the fundamental questions in the theory of deformed transforms is to investigate basic properties of the kernel
![]() $B_{\kappa ,a}(x,y)$
, in particular, to know when it is uniformly bounded. To illustrate the importance of this property, note that the condition
$B_{\kappa ,a}(x,y)$
, in particular, to know when it is uniformly bounded. To illustrate the importance of this property, note that the condition
![]() $|B_{\kappa ,a}(x,y)|\le M$
implies the Hausdorff-Young inequality
$|B_{\kappa ,a}(x,y)|\le M$
implies the Hausdorff-Young inequality
A more important problem is to describe parameters so that there holds
In this case, the Hausdorff-Young inequality holds with the constant
![]() $1$
and one can define the generalized translation operator
$1$
and one can define the generalized translation operator
![]() $\tau ^yf(x)$
in
$\tau ^yf(x)$
in
![]() $L^{2}(\mathbb {R}^{d},d\mu _{k,a})$
by
$L^{2}(\mathbb {R}^{d},d\mu _{k,a})$
by
(see [Reference Gorbachev, Ivanov and Tikhonov15]), and moreover, its norm equals 1.
Let us list the known cases when (1.2) holds:
-
• for
 $a=2$
[Reference Rösler22] (
$a=2$
[Reference Rösler22] (
 $\mathcal {F}_{\kappa ,2}$
reduces to the Dunkl transform);
$\mathcal {F}_{\kappa ,2}$
reduces to the Dunkl transform); -
• for
 $a=1$
and
$a=1$
and
 $d=1$
,
$d=1$
,
 $\langle \kappa \rangle \ge 1/2$
[Reference Gorbachev, Ivanov and Tikhonov15, Section 6] Footnote
1
;
$\langle \kappa \rangle \ge 1/2$
[Reference Gorbachev, Ivanov and Tikhonov15, Section 6] Footnote
1
; -
• for
 $a=1$
and
$a=1$
and
 $d\ge 2$
,
$d\ge 2$
,
 $\langle \kappa \rangle \ge 0$
[Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.11];
$\langle \kappa \rangle \ge 0$
[Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.11]; -
• for
 $\frac {2}{a}\in \mathbb {N}$
and
$\frac {2}{a}\in \mathbb {N}$
and
 $d\ge 2$
,
$d\ge 2$
,
 $ \langle \kappa \rangle \ge 0$
[Reference De Bie5, Reference Constales, De Bie and Lian10] Footnote
2
.
$ \langle \kappa \rangle \ge 0$
[Reference De Bie5, Reference Constales, De Bie and Lian10] Footnote
2
.
In this paper, we continue to study the case
Its importance was discussed in [Reference Ben Saïd, Kobayashi and Ørsted4], [Reference Boubatra, Negzaoui and Sifi7], and [Reference Constales, De Bie and Lian10]. For example, in this case, one has a simple inversion formula for the
![]() $(\kappa ,a)$
-generalized Fourier transform [Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.3] and an explicit expression for the generalized translation operator
$(\kappa ,a)$
-generalized Fourier transform [Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.3] and an explicit expression for the generalized translation operator
![]() $\tau ^y$
[Reference Boubatra, Negzaoui and Sifi7]. Moreover, the kernel
$\tau ^y$
[Reference Boubatra, Negzaoui and Sifi7]. Moreover, the kernel
![]() $B_{\kappa ,2/n}$
with
$B_{\kappa ,2/n}$
with
![]() $n\in \mathbb {N}$
appears for dihedral groups G [Reference Constales, De Bie and Lian10].
$n\in \mathbb {N}$
appears for dihedral groups G [Reference Constales, De Bie and Lian10].
Our first goal in this paper is, on the one hand, to extend the list of parameters for which (1.2) holds for
![]() $\frac {2}{a}\in \mathbb {N}$
; on the other hand, to point out the cases when (1.2) does not hold. The following theorem describes positive results, where, for completeness, we include all known cases.
$\frac {2}{a}\in \mathbb {N}$
; on the other hand, to point out the cases when (1.2) does not hold. The following theorem describes positive results, where, for completeness, we include all known cases.
Theorem 1.1 (see [Reference Constales, De Bie and Lian10,
 $d\ge 2$
]).
$d\ge 2$
]).
Let
![]() $0<a\le 1$
,
$0<a\le 1$
,
![]() $\frac {2}{a}\in \mathbb {N}$
. If
$\frac {2}{a}\in \mathbb {N}$
. If
![]() $d=1$
,
$d=1$
,
![]() $\langle \kappa \rangle \ge \frac {1}{2}$
or
$\langle \kappa \rangle \ge \frac {1}{2}$
or
![]() $d\ge 2$
,
$d\ge 2$
,
![]() $\langle \kappa \rangle \ge 0$
, then equality (1.2) is true.
$\langle \kappa \rangle \ge 0$
, then equality (1.2) is true.
Our proof of Theorem 1.1 for
![]() $d=1$
is based on an integral representation of
$d=1$
is based on an integral representation of
![]() $B_{\kappa ,a}$
with the special kernel and a study of positiveness of this kernel. This approach is closely related to the theory of positive definite functions.
$B_{\kappa ,a}$
with the special kernel and a study of positiveness of this kernel. This approach is closely related to the theory of positive definite functions.
In the general case
![]() $d\ge 1$
, we give the proof based on the approach developed in the papers [Reference De Bie and Lian6, Reference Constales, De Bie and Lian10, Reference Deleaval and Demni11], see Section 4.1, and the alternative proof based on representation with positive kernels, see Subsection 4.3.
$d\ge 1$
, we give the proof based on the approach developed in the papers [Reference De Bie and Lian6, Reference Constales, De Bie and Lian10, Reference Deleaval and Demni11], see Section 4.1, and the alternative proof based on representation with positive kernels, see Subsection 4.3.
With regard to negative results, we obtain the following theorem, where we specify parameters when Theorem 1.1 does not hold.
Theorem 1.2. In either of the following cases:
-
•
 $d=1$
,
$d=1$
,
 $0<a\le 1$
, and
$0<a\le 1$
, and
 $\langle \kappa \rangle =\frac {1}{2}-\frac {a}{4}$
, or
$\langle \kappa \rangle =\frac {1}{2}-\frac {a}{4}$
, or -
•
 $d\ge 1$
,
$d\ge 1$
,
 $a\in (1,2)\cup (2,\infty )$
and
$a\in (1,2)\cup (2,\infty )$
and
 $\langle \kappa \rangle \ge 0$
,
$\langle \kappa \rangle \ge 0$
,
we have
The rest of the paper is organized as follows. Section 2 is devoted to the proof of Theorem 1.1 in the case
![]() $d=1$
. In Section 3, we study the properties of the one-dimensional kernel
$d=1$
. In Section 3, we study the properties of the one-dimensional kernel
![]() $B_{\kappa ,a}$
for
$B_{\kappa ,a}$
for
![]() $\lambda _{\kappa ,a}<0$
. In particular, in Section 3.1, we investigate positive definiteness of kernels of the integral transforms generated by
$\lambda _{\kappa ,a}<0$
. In particular, in Section 3.1, we investigate positive definiteness of kernels of the integral transforms generated by
![]() ${\mathcal {F}}_{\kappa ,a}$
. In Section 4, we prove Theorem 1.1 in full generality as well as Theorem 1.2 (Section 4.3).
${\mathcal {F}}_{\kappa ,a}$
. In Section 4, we prove Theorem 1.1 in full generality as well as Theorem 1.2 (Section 4.3).
In Section 5, we study the question of how the
![]() $\mathcal {F}_{\kappa ,a}$
transform acts on Schwartz functions. The Schwartz space
$\mathcal {F}_{\kappa ,a}$
transform acts on Schwartz functions. The Schwartz space
![]() $\mathcal {S}(\mathbb {R}^{d})$
is invariant under the classical Fourier transform
$\mathcal {S}(\mathbb {R}^{d})$
is invariant under the classical Fourier transform
![]() $\mathcal {F}_{0,2}$
and the Dunkl
$\mathcal {F}_{0,2}$
and the Dunkl
![]() $\mathcal {F}_{\kappa ,2}$
(see [Reference de Jeu8]), but the case of deformed transforms is more complicated. In fact, we show that
$\mathcal {F}_{\kappa ,2}$
(see [Reference de Jeu8]), but the case of deformed transforms is more complicated. In fact, we show that
![]() $\mathcal {S}(\mathbb {R}^d)$
is not invariant under
$\mathcal {S}(\mathbb {R}^d)$
is not invariant under
![]() $\mathcal {F}_{\kappa ,a}$
for
$\mathcal {F}_{\kappa ,a}$
for
![]() $a\neq 2$
, which contradicts a widely used statement in [Reference Johansen18] (see Remark 5.3). If
$a\neq 2$
, which contradicts a widely used statement in [Reference Johansen18] (see Remark 5.3). If
![]() $\frac {a}{2}\notin \mathbb {N}$
, then the generalized Fourier transform may not be infinitely differentiable, and if
$\frac {a}{2}\notin \mathbb {N}$
, then the generalized Fourier transform may not be infinitely differentiable, and if
![]() $\frac {2}{a}\notin \mathbb {N}$
, then it may not be rapidly decreasing at infinity. For
$\frac {2}{a}\notin \mathbb {N}$
, then it may not be rapidly decreasing at infinity. For
![]() $d=1$
and
$d=1$
and
![]() $\frac {2}{a}\in \mathbb {N}$
, the generalized Fourier transform of
$\frac {2}{a}\in \mathbb {N}$
, the generalized Fourier transform of
![]() $f\in \mathcal {S}(\mathbb {R})$
is rapidly decreasing due to the representation
$f\in \mathcal {S}(\mathbb {R})$
is rapidly decreasing due to the representation
![]() $\mathcal {F}_{\kappa ,a}(f)(y)=F_1\bigl (|y|^{a/2}\bigr )+yF_2\bigl (|y|^{a/2}\bigr )$
, where the even functions
$\mathcal {F}_{\kappa ,a}(f)(y)=F_1\bigl (|y|^{a/2}\bigr )+yF_2\bigl (|y|^{a/2}\bigr )$
, where the even functions
![]() $F_1,F_2\in \mathcal {S}(\mathbb {R})$
(see Proposition 5.4).
$F_1,F_2\in \mathcal {S}(\mathbb {R})$
(see Proposition 5.4).
Finally, in Section 6, we study one-dimensional nondeformed unitary transforms generated by
![]() $\mathcal {F}_{\kappa ,a}$
:
$\mathcal {F}_{\kappa ,a}$
:
 $$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)=\int_{-\infty}^{\infty}e_{2r+1}(uv,\lambda)g(u)\,\frac{|u|^{2\lambda+1} \,du}{2^{\lambda+1}\Gamma(\lambda+1)}, \end{align*} $$
$$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)=\int_{-\infty}^{\infty}e_{2r+1}(uv,\lambda)g(u)\,\frac{|u|^{2\lambda+1} \,du}{2^{\lambda+1}\Gamma(\lambda+1)}, \end{align*} $$
where
![]() $r\in \mathbb {Z}_+$
,
$r\in \mathbb {Z}_+$
,
![]() $\lambda \ge -1/2$
, and the kernel
$\lambda \ge -1/2$
, and the kernel
 $$\begin{align*}e_{2r+1}(uv,\lambda)=j_{\lambda}(uv)+i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(uv) \end{align*}$$
$$\begin{align*}e_{2r+1}(uv,\lambda)=j_{\lambda}(uv)+i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(uv) \end{align*}$$
is an eigenfunction of the differential-difference operator
Here,
![]() $\Delta _{\lambda +1/2}$
is the one-dimensional Dunkl Laplacian for
$\Delta _{\lambda +1/2}$
is the one-dimensional Dunkl Laplacian for
![]() $\langle \kappa \rangle =\lambda +\frac {1}{2}$
and
$\langle \kappa \rangle =\lambda +\frac {1}{2}$
and
is the Pochhammer symbol. Note that such unitary transforms give new examples of an important class of Bessel-Hankel type transforms with the kernel
![]() $k(uv)$
(see, e.g. [Reference Titchmarsh24, Chapter VIII]). In particular, they generalize the one-dimensional Dunkl transform (
$k(uv)$
(see, e.g. [Reference Titchmarsh24, Chapter VIII]). In particular, they generalize the one-dimensional Dunkl transform (
![]() $r=0$
).
$r=0$
).
2 Proof of Theorem 1.1 in the one-dimensional case
In what follows, we assume that
and
![]() $\mathcal {F}_{\kappa ,a}$
is the
$\mathcal {F}_{\kappa ,a}$
is the
![]() $(\kappa ,a)$
-generalized Fourier transform (1.1) on the real line. Firstly, let us investigate when the kernel of
$(\kappa ,a)$
-generalized Fourier transform (1.1) on the real line. Firstly, let us investigate when the kernel of
![]() $\mathcal {F}_{\kappa ,a}$
is uniformly bounded. Using [Reference Ben Saïd, Kobayashi and Ørsted4, Section 5], we can write the kernel as
$\mathcal {F}_{\kappa ,a}$
is uniformly bounded. Using [Reference Ben Saïd, Kobayashi and Ørsted4, Section 5], we can write the kernel as
where
![]() $j_{\lambda }(x)=2^{\lambda }\Gamma (\lambda +1)x^{-\lambda }J_{\lambda }(x)$
is the normalized Bessel function and
$j_{\lambda }(x)=2^{\lambda }\Gamma (\lambda +1)x^{-\lambda }J_{\lambda }(x)$
is the normalized Bessel function and
![]() $J_{\lambda }(x)$
is the classical Bessel function. Then the asymptotic behavior of
$J_{\lambda }(x)$
is the classical Bessel function. Then the asymptotic behavior of
![]() $J_{\lambda }(x)$
(see [Reference Watson25, Chapter VII, 7.1]) immediately allows us to derive the following
$J_{\lambda }(x)$
(see [Reference Watson25, Chapter VII, 7.1]) immediately allows us to derive the following
Proposition 2.1. Let
![]() $d=1$
. The conditions
$d=1$
. The conditions
are necessary and sufficient for boundedness of the kernel
![]() $B_{\kappa ,a}(x,y)$
.
$B_{\kappa ,a}(x,y)$
.
The main goal of this section is to prove Theorem 1.1 for
![]() $d=1$
.
$d=1$
.
Proof. Note that
![]() $B_{\kappa ,a}(x,y)=b_{\kappa ,a}(xy)$
, where
$B_{\kappa ,a}(x,y)=b_{\kappa ,a}(xy)$
, where
Therefore, under the conditions of Theorem 1.1, it suffices to establish the inequality
![]() $|b_{\kappa ,a}(x)|\le 1$
for
$|b_{\kappa ,a}(x)|\le 1$
for
![]() $x\in \mathbb {R}$
.
$x\in \mathbb {R}$
.
Let
![]() $a=\frac {2}{R}$
,
$a=\frac {2}{R}$
,
![]() $R\in \mathbb {N}$
. Equality (2.3) can be written as
$R\in \mathbb {N}$
. Equality (2.3) can be written as
Let
![]() $x\in \mathbb {R}$
. In the case
$x\in \mathbb {R}$
. In the case
![]() $R=2r+1$
,
$R=2r+1$
,
![]() $a=\frac {2}{2r+1}$
,
$a=\frac {2}{2r+1}$
,
![]() $r\in \mathbb {Z}_{+}$
, and Footnote
3
$r\in \mathbb {Z}_{+}$
, and Footnote
3
![]() $v=(2r+1)x^{\frac {1}{2r+1}}$
,
$v=(2r+1)x^{\frac {1}{2r+1}}$
,
![]() $x=\bigl (\frac {v}{2r+1}\bigr )^{2r+1}$
, there holds
$x=\bigl (\frac {v}{2r+1}\bigr )^{2r+1}$
, there holds
 $$ \begin{align} e_{2r+1}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{v}{2r+1}\Bigr)^{2r+1}\Bigr)=j_{\lambda}(v)+ i(-1)^{r+1}\,\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(v). \end{align} $$
$$ \begin{align} e_{2r+1}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{v}{2r+1}\Bigr)^{2r+1}\Bigr)=j_{\lambda}(v)+ i(-1)^{r+1}\,\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(v). \end{align} $$
In the case
![]() $R=2r$
,
$R=2r$
,
![]() $a=\frac {1}{r}$
,
$a=\frac {1}{r}$
,
![]() $r\in \mathbb {N}$
, and
$r\in \mathbb {N}$
, and
![]() $v=2r|x|^{\frac {1}{2r}}{\operatorname{sign}} {}\ x$
,
$v=2r|x|^{\frac {1}{2r}}{\operatorname{sign}} {}\ x$
,
![]() $x=\big (\frac {v}{2r}\big )^{2r}{\operatorname{sign}} {}\ v$
, we have
$x=\big (\frac {v}{2r}\big )^{2r}{\operatorname{sign}} {}\ v$
, we have
 $$ \begin{align} e_{2r}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{v}{2r}\Bigr)^{2r}{\operatorname{sign}}{}\ v\Bigr)=j_{\lambda}(v)+ (-1)^{r}\,\frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)\,{\operatorname{sign}}{}\ v. \end{align} $$
$$ \begin{align} e_{2r}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{v}{2r}\Bigr)^{2r}{\operatorname{sign}}{}\ v\Bigr)=j_{\lambda}(v)+ (-1)^{r}\,\frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)\,{\operatorname{sign}}{}\ v. \end{align} $$
In order to see that
![]() $|e_{2r+1}(v,\lambda )|, |e_{2r}(v,\lambda )|\le 1$
, we will need several auxiliary results. We start with the following identity
$|e_{2r+1}(v,\lambda )|, |e_{2r}(v,\lambda )|\le 1$
, we will need several auxiliary results. We start with the following identity
 $$ \begin{align} \frac{v^2}{4(\lambda+1)(\lambda+2)}\,j_{\lambda+2}(v)=j_{\lambda+1}(v)-j_{\lambda}(v), \end{align} $$
$$ \begin{align} \frac{v^2}{4(\lambda+1)(\lambda+2)}\,j_{\lambda+2}(v)=j_{\lambda+1}(v)-j_{\lambda}(v), \end{align} $$
which follows from the recurrence relation for the Bessel function
![]() $J_{\lambda }(v)$
(see [Reference Watson25, Chapter III, 3.2]). Then, by induction, we establish
$J_{\lambda }(v)$
(see [Reference Watson25, Chapter III, 3.2]). Then, by induction, we establish
Lemma 2.2. If
![]() $r\in \mathbb {N}$
, then
$r\in \mathbb {N}$
, then
 $$ \begin{align} \frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)= (-1)^{r}j_{\lambda}(v)+\sum_{s=1}^{r-1}(-1)^{s+r} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}\,j_{\lambda+s}(v) +\frac{(\lambda+r+1)_{r-1}}{(\lambda+1)_{r-1}}\,j_{\lambda+r}(v). \end{align} $$
$$ \begin{align} \frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)= (-1)^{r}j_{\lambda}(v)+\sum_{s=1}^{r-1}(-1)^{s+r} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}\,j_{\lambda+s}(v) +\frac{(\lambda+r+1)_{r-1}}{(\lambda+1)_{r-1}}\,j_{\lambda+r}(v). \end{align} $$
Proof. For
![]() $r=1$
, the needed formula coincides with (2.6). Assume that (2.7) is valid for every
$r=1$
, the needed formula coincides with (2.6). Assume that (2.7) is valid for every
![]() $k\le r-1$
and
$k\le r-1$
and
![]() $\lambda $
. Denote by
$\lambda $
. Denote by
![]() $a_{s}^r(\lambda )$
,
$a_{s}^r(\lambda )$
,
![]() $s=0,1,\dots ,r$
, the coefficients by
$s=0,1,\dots ,r$
, the coefficients by
![]() $j_{\lambda +s}(v)$
in the decomposition (2.7). Taking into account (2.6) and the inductive assumption, we derive that
$j_{\lambda +s}(v)$
in the decomposition (2.7). Taking into account (2.6) and the inductive assumption, we derive that
 $$ \begin{align*} \frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)&= \frac{v^{2r-2}}{2^{2r-2}(\lambda+1)_{2r-2}}\,\frac{v^2}{4(\lambda+2r-1)(\lambda+2r)}\,j_{(\lambda+2r-2)+2}(v)\\ &=\frac{v^{2r-2}}{2^{2r-2}(\lambda+1)_{2r-2}}\,\{j_{(\lambda+1)+2r-2}(v)-j_{\lambda+2r-2}(v)\}\\ &=\frac{\lambda+2r-1}{\lambda+1}\sum_{s=1}^{r}a_{s-1}^{r-1}(\lambda+1)j_{\lambda+s}(v)- \sum_{s=0}^{r-1}a_{s}^{r-1}(\lambda)j_{\lambda+s}(v). \end{align*} $$
$$ \begin{align*} \frac{v^{2r}}{2^{2r}(\lambda+1)_{2r}}\,j_{\lambda+2r}(v)&= \frac{v^{2r-2}}{2^{2r-2}(\lambda+1)_{2r-2}}\,\frac{v^2}{4(\lambda+2r-1)(\lambda+2r)}\,j_{(\lambda+2r-2)+2}(v)\\ &=\frac{v^{2r-2}}{2^{2r-2}(\lambda+1)_{2r-2}}\,\{j_{(\lambda+1)+2r-2}(v)-j_{\lambda+2r-2}(v)\}\\ &=\frac{\lambda+2r-1}{\lambda+1}\sum_{s=1}^{r}a_{s-1}^{r-1}(\lambda+1)j_{\lambda+s}(v)- \sum_{s=0}^{r-1}a_{s}^{r-1}(\lambda)j_{\lambda+s}(v). \end{align*} $$
It is enough to show that
Indeed, using the induction step, we have that
and, for
![]() $s=1,\dots ,r-1$
,
$s=1,\dots ,r-1$
,
 $$ \begin{align*} a_s^r(\lambda)&=(-1)^{s+r}\Bigl\{\frac{\lambda+2r-1}{\lambda+1} \binom{r-1}{s-1}\frac{(\lambda+r)_{s-1}}{(\lambda+2)_{s-1}}+\binom{r-1}{s}\frac{(\lambda+r-1)_{s}}{(\lambda+1)_{s}}\Bigr\} \\[4pt] &=(-1)^{s+r}\binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}\Bigl\{\frac{\lambda+2r-1}{\lambda+r+s-1}\,\frac{s}{r}+ \frac{\lambda+r-1}{\lambda+r+s-1}\,\frac{r-s}{r}\Bigr\}\\[4pt] &=(-1)^{s+r}\binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}, \end{align*} $$
$$ \begin{align*} a_s^r(\lambda)&=(-1)^{s+r}\Bigl\{\frac{\lambda+2r-1}{\lambda+1} \binom{r-1}{s-1}\frac{(\lambda+r)_{s-1}}{(\lambda+2)_{s-1}}+\binom{r-1}{s}\frac{(\lambda+r-1)_{s}}{(\lambda+1)_{s}}\Bigr\} \\[4pt] &=(-1)^{s+r}\binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}\Bigl\{\frac{\lambda+2r-1}{\lambda+r+s-1}\,\frac{s}{r}+ \frac{\lambda+r-1}{\lambda+r+s-1}\,\frac{r-s}{r}\Bigr\}\\[4pt] &=(-1)^{s+r}\binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1)_{s}}, \end{align*} $$
which completes the proof.
Lemma 2.3. For
![]() $r\in \mathbb {Z}_{+}$
, we have
$r\in \mathbb {Z}_{+}$
, we have
 $$\begin{align*}\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\,j_{\lambda+2r+1}(v)=(-1)^{r+1}\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1)_{s}}\,j_{\lambda+s}'(v). \end{align*}$$
$$\begin{align*}\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\,j_{\lambda+2r+1}(v)=(-1)^{r+1}\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1)_{s}}\,j_{\lambda+s}'(v). \end{align*}$$
Proof. Using Lemma 2.2 and the equality
we derive that
 $$ \begin{align*} &\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\,j_{\lambda+2r+1}(v)=\frac{v}{2(\lambda+1)}\, \frac{v^{2r}}{2^{2r}(\lambda+2)_{2r}}\,j_{(\lambda+1)+2r}(v)\\ &\quad =\frac{v}{2(\lambda+1)}\Bigl\{(-1)^{r}j_{\lambda+1}(v)+\sum_{s=1}^{r-1}(-1)^{s+r} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda +2)_{s}}\,j_{\lambda+1+s}(v)+ \frac{(\lambda+r+2)_{r-1}}{(\lambda+2)_{r-1}}\,j_{\lambda+1+r}(v)\Bigr\}\\ &\qquad\qquad\qquad\qquad = (-1)^{r+1}j_{\lambda}'(v)+\sum_{s=1}^{r-1}(-1)^{s+r+1} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1)_s}\,j_{\lambda+s}'(v)- \frac{(\lambda+r+1)_{r}}{(\lambda+1)_r}\,j_{\lambda+r}'(v). \end{align*} $$
$$ \begin{align*} &\frac{v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\,j_{\lambda+2r+1}(v)=\frac{v}{2(\lambda+1)}\, \frac{v^{2r}}{2^{2r}(\lambda+2)_{2r}}\,j_{(\lambda+1)+2r}(v)\\ &\quad =\frac{v}{2(\lambda+1)}\Bigl\{(-1)^{r}j_{\lambda+1}(v)+\sum_{s=1}^{r-1}(-1)^{s+r} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda +2)_{s}}\,j_{\lambda+1+s}(v)+ \frac{(\lambda+r+2)_{r-1}}{(\lambda+2)_{r-1}}\,j_{\lambda+1+r}(v)\Bigr\}\\ &\qquad\qquad\qquad\qquad = (-1)^{r+1}j_{\lambda}'(v)+\sum_{s=1}^{r-1}(-1)^{s+r+1} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1)_s}\,j_{\lambda+s}'(v)- \frac{(\lambda+r+1)_{r}}{(\lambda+1)_r}\,j_{\lambda+r}'(v). \end{align*} $$
Taking into account (2.4) and (2.5), Lemmas 2.2 and 2.3, and
 $$ \begin{align} j_{\lambda}(v)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}e^{-ivt}\,dt,\quad j_{\lambda}'(v)=-ic_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}te^{-ivt}\,dt \end{align} $$
$$ \begin{align} j_{\lambda}(v)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}e^{-ivt}\,dt,\quad j_{\lambda}'(v)=-ic_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}te^{-ivt}\,dt \end{align} $$
with
![]() $c_{\lambda }=\frac {\Gamma (\lambda +1)}{\sqrt {\pi }\Gamma (\lambda +1/2)}$
,
$c_{\lambda }=\frac {\Gamma (\lambda +1)}{\sqrt {\pi }\Gamma (\lambda +1/2)}$
,
![]() $\lambda>-1/2$
(see [Reference Watson25, Chapter III, 3.3], we arrive at the following integral representations of the functions
$\lambda>-1/2$
(see [Reference Watson25, Chapter III, 3.3], we arrive at the following integral representations of the functions
![]() $e_{2r+1}(v,\lambda )$
, and
$e_{2r+1}(v,\lambda )$
, and
![]() $e_{2r}(v,\lambda )$
.
$e_{2r}(v,\lambda )$
.
Lemma 2.4. If
![]() $r\in \mathbb {Z}_{+}$
,
$r\in \mathbb {Z}_{+}$
,
![]() $\lambda>-1/2$
, then
$\lambda>-1/2$
, then
 $$ \begin{align} e_{2r+1}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}q_{2r+1}(t,\lambda)e^{-ivt}\,dt, \end{align} $$
$$ \begin{align} e_{2r+1}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}q_{2r+1}(t,\lambda)e^{-ivt}\,dt, \end{align} $$
where
![]() $q_{2r+1}(t,\lambda )$
is a polynomial of degree
$q_{2r+1}(t,\lambda )$
is a polynomial of degree
![]() $2r+1$
with respect to t given by
$2r+1$
with respect to t given by
 $$\begin{align*}q_{2r+1}(t,\lambda)=1+t\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s. \end{align*}$$
$$\begin{align*}q_{2r+1}(t,\lambda)=1+t\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s. \end{align*}$$
Lemma 2.5. If
![]() $r\in \mathbb {N}$
,
$r\in \mathbb {N}$
,
![]() $\lambda>-1/2$
, then
$\lambda>-1/2$
, then
 $$ \begin{align*} e_{2r}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}q_{2r}(t,\lambda)e^{-ivt}\,dt, \end{align*} $$
$$ \begin{align*} e_{2r}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}q_{2r}(t,\lambda)e^{-ivt}\,dt, \end{align*} $$
where
![]() $q_{2r}(t,\lambda )$
is a polynomial of degree
$q_{2r}(t,\lambda )$
is a polynomial of degree
![]() $2r$
with respect to t given by
$2r$
with respect to t given by
 $$\begin{align*}q_{2r}(t,\lambda)=q_{2r}(t,v,\lambda) =1+{\operatorname{sign}}{}\ v\,\Bigl\{\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s\Bigr\}. \end{align*}$$
$$\begin{align*}q_{2r}(t,\lambda)=q_{2r}(t,v,\lambda) =1+{\operatorname{sign}}{}\ v\,\Bigl\{\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s\Bigr\}. \end{align*}$$
For our further analysis, it is important to know for which
![]() $\lambda $
the polynomials
$\lambda $
the polynomials
![]() $q_{2r}(t,\lambda )$
,
$q_{2r}(t,\lambda )$
,
![]() $q_{2r+1}(t,\lambda )$
are nonnegative on
$q_{2r+1}(t,\lambda )$
are nonnegative on
![]() $[-1,1]$
. If
$[-1,1]$
. If
![]() $r=0$
,
$r=0$
,
![]() $q_{1}(t,\lambda )=1-t\ge 0$
on
$q_{1}(t,\lambda )=1-t\ge 0$
on
![]() $[-1,1]$
, that is,
$[-1,1]$
, that is,
![]() $q_{1}$
does not depend on
$q_{1}$
does not depend on
![]() $\lambda $
. This special case corresponds to parameters
$\lambda $
. This special case corresponds to parameters
![]() $a=2,\, \kappa \ge 0$
, and hence (2.9) is a well-known integral representation of the kernel of the one-dimensional Dunkl transform. In other cases, positivity conditions for
$a=2,\, \kappa \ge 0$
, and hence (2.9) is a well-known integral representation of the kernel of the one-dimensional Dunkl transform. In other cases, positivity conditions for
![]() $q_{2r}(t,\lambda )$
and
$q_{2r}(t,\lambda )$
and
![]() $q_{2r+1}(t,\lambda )$
depend on
$q_{2r+1}(t,\lambda )$
depend on
![]() $\lambda $
. We will see that there holds
$\lambda $
. We will see that there holds
where
![]() $\{P_n^{(\alpha )}(t)\}_{n=0}^{\infty }$
is the system of Gegenbauer (ultraspherical) polynomials, that is, the family of polynomials orthogonal on
$\{P_n^{(\alpha )}(t)\}_{n=0}^{\infty }$
is the system of Gegenbauer (ultraspherical) polynomials, that is, the family of polynomials orthogonal on
![]() $[-1,1]$
with respect to the weight function
$[-1,1]$
with respect to the weight function
![]() $(1-t^2)^{\alpha }$
,
$(1-t^2)^{\alpha }$
,
![]() $\alpha>-1$
, normalized by
$\alpha>-1$
, normalized by
![]() $P_n^{(\alpha )}(1)=1$
. Note that,
$P_n^{(\alpha )}(1)=1$
. Note that,
![]() $P_n^{(-1/2)}(t)=\cos {}(n\arccos t)$
are the Chebyshev polynomials. For
$P_n^{(-1/2)}(t)=\cos {}(n\arccos t)$
are the Chebyshev polynomials. For
![]() $\lambda>-1/2$
, we have
$\lambda>-1/2$
, we have
where
![]() $C_n^{\lambda }(t)$
are the Gegenbauer polynomials given in [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9].
$C_n^{\lambda }(t)$
are the Gegenbauer polynomials given in [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9].
Lemma 2.6. For
![]() $\lambda>-1/2$
and
$\lambda>-1/2$
and
![]() $r\ge 0$
, there hold
$r\ge 0$
, there hold
 $$ \begin{align*} P_{2r}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s \end{align*} $$
$$ \begin{align*} P_{2r}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s \end{align*} $$
and
 $$ \begin{align*} P_{2r+1}^{(\lambda-1/2)}(t)=t\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s. \end{align*} $$
$$ \begin{align*} P_{2r+1}^{(\lambda-1/2)}(t)=t\sum_{s=0}^{r}(-1)^{s} \binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s. \end{align*} $$
Therefore, (2.10) holds.
Proof. Since
![]() $ \frac {(-r)_s}{s!}=(-1)^{s}\binom {r}{s}, $
taking into account (2.11), [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9(21)], we get
$ \frac {(-r)_s}{s!}=(-1)^{s}\binom {r}{s}, $
taking into account (2.11), [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9(21)], we get
 $$ \begin{align*} \sum_{s=0}^{r}(-1)^{s}\binom{r}{s}&\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s =\sum_{s=0}^{r}\frac{(-r)_s(\lambda+r)_{s}}{s!\,(\lambda+1/2)_{s}}\,(1-t^2)^s\\ &\qquad\quad ={}_{2}F_1(-r,\lambda+r;\lambda+1/2;1-t^2)=\frac{(2r)!\,\Gamma(2\lambda+1)} {2\Gamma(2\lambda+2r)}\,\frac{1}{\lambda}\,C_{2r}^{\lambda}(t)=P_{2r}^{(\lambda-1/2)}(t). \end{align*} $$
$$ \begin{align*} \sum_{s=0}^{r}(-1)^{s}\binom{r}{s}&\frac{(\lambda+r)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s =\sum_{s=0}^{r}\frac{(-r)_s(\lambda+r)_{s}}{s!\,(\lambda+1/2)_{s}}\,(1-t^2)^s\\ &\qquad\quad ={}_{2}F_1(-r,\lambda+r;\lambda+1/2;1-t^2)=\frac{(2r)!\,\Gamma(2\lambda+1)} {2\Gamma(2\lambda+2r)}\,\frac{1}{\lambda}\,C_{2r}^{\lambda}(t)=P_{2r}^{(\lambda-1/2)}(t). \end{align*} $$
Similarly, using (2.11), [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9(22)], we arrive at
 $$ \begin{align*} t\sum_{s=0}^{r}(-1)^{s}&\binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s =t\sum_{s=0}^{r}\frac{(-r)_s(\lambda+r+1)_{s}}{s!\,(\lambda+1/2)_{s}}\,(1-t^2)^s\\ &=t\,{}_{2}F_1(-r,\lambda+r+1;\lambda+1/2;1-t^2)=\frac{(2r+1)!\,\Gamma(2\lambda+1)} {2\Gamma(2\lambda+2r+1)}\,\frac{1}{\lambda}\,C_{2r+1}^{\lambda}(t)=P_{2r+1}^{(\lambda-1/2)}(t). \end{align*} $$
$$ \begin{align*} t\sum_{s=0}^{r}(-1)^{s}&\binom{r}{s}\frac{(\lambda+r+1)_{s}}{(\lambda+1/2)_{s}}\,(1-t^2)^s =t\sum_{s=0}^{r}\frac{(-r)_s(\lambda+r+1)_{s}}{s!\,(\lambda+1/2)_{s}}\,(1-t^2)^s\\ &=t\,{}_{2}F_1(-r,\lambda+r+1;\lambda+1/2;1-t^2)=\frac{(2r+1)!\,\Gamma(2\lambda+1)} {2\Gamma(2\lambda+2r+1)}\,\frac{1}{\lambda}\,C_{2r+1}^{\lambda}(t)=P_{2r+1}^{(\lambda-1/2)}(t). \end{align*} $$
We complete the proof of Theorem 1.1 noting that
![]() $|P_{n}^{(\lambda -1/2)}(t)|\le 1$
for
$|P_{n}^{(\lambda -1/2)}(t)|\le 1$
for
![]() $t\in [-1,1]$
under the condition
$t\in [-1,1]$
under the condition
![]() $\lambda \ge 0$
or, equivalently,
$\lambda \ge 0$
or, equivalently,
![]() $\kappa \ge 1/2$
(see [Reference Szegö23, Chapter VII, 7.32.2]). Then in light of Remark 3.2 below and Lemma 2.6, the polynomials
$\kappa \ge 1/2$
(see [Reference Szegö23, Chapter VII, 7.32.2]). Then in light of Remark 3.2 below and Lemma 2.6, the polynomials
![]() $q_{2r}(t,\lambda )$
and
$q_{2r}(t,\lambda )$
and
![]() $q_{2r+1}(t,\lambda )$
are nonnegative on
$q_{2r+1}(t,\lambda )$
are nonnegative on
![]() $[-1,1]$
and therefore Lemmas 2.4 and 2.5, together with (2.4) and (2.5), yield the statement of Theorem 1.1. To illustrate this, for
$[-1,1]$
and therefore Lemmas 2.4 and 2.5, together with (2.4) and (2.5), yield the statement of Theorem 1.1. To illustrate this, for
![]() $a=\frac {2}{2r+1}$
,
$a=\frac {2}{2r+1}$
,
![]() $v=(2r+1)x^{\frac {1}{2r+1}}$
, we have
$v=(2r+1)x^{\frac {1}{2r+1}}$
, we have
The following integral representations of the kernel
![]() $B_{\kappa ,a}(x,y)$
follow from the lemmas above.
$B_{\kappa ,a}(x,y)$
follow from the lemmas above.
Corollary 2.7. If
![]() $\lambda =(2\kappa -1)/a$
and
$\lambda =(2\kappa -1)/a$
and
![]() $\kappa>\frac {1}{2}-\frac {a}{4}$
, then for
$\kappa>\frac {1}{2}-\frac {a}{4}$
, then for
![]() $x\in \mathbb {R}$
$x\in \mathbb {R}$
 $$\begin{align*}B_{\kappa,a}(x,y)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))e^{-i(2r+1)(xy)^{\frac{1}{2r+1}}{}t}\,dt,\quad a=\frac{2}{2r+1},\quad r\in\mathbb{Z}_+, \end{align*}$$
$$\begin{align*}B_{\kappa,a}(x,y)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))e^{-i(2r+1)(xy)^{\frac{1}{2r+1}}{}t}\,dt,\quad a=\frac{2}{2r+1},\quad r\in\mathbb{Z}_+, \end{align*}$$
and
 $$\begin{align*}B_{\kappa,a}(x,y)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+{\operatorname{sign}}{}\ (xy)\,P_{2r}^{(\lambda-1/2)}(t))e^{-i(2r|xy|^{\frac{1}{2r}}{\operatorname{sign}}{}\ (xy))t}\,dt,\quad a=\frac{1}{r},\quad r\in\mathbb{N}. \end{align*}$$
$$\begin{align*}B_{\kappa,a}(x,y)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+{\operatorname{sign}}{}\ (xy)\,P_{2r}^{(\lambda-1/2)}(t))e^{-i(2r|xy|^{\frac{1}{2r}}{\operatorname{sign}}{}\ (xy))t}\,dt,\quad a=\frac{1}{r},\quad r\in\mathbb{N}. \end{align*}$$
Remark 2.8. The representations of
![]() $B_{\kappa ,a}(x,y)$
given in Corollary 2.7 can be also obtained from
$B_{\kappa ,a}(x,y)$
given in Corollary 2.7 can be also obtained from
(see [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter X, 10.9(38)]) without applying Lemmas 2.2 and 2.3. These lemmas are of independent interest.
Remark 2.9. The positiveness of the polynomials
![]() $q_{2r}(t,\lambda )$
,
$q_{2r}(t,\lambda )$
,
![]() $q_{2r+1}(t,\lambda )$
is sufficient, but not necessary, for the estimate
$q_{2r+1}(t,\lambda )$
is sufficient, but not necessary, for the estimate
![]() $|B_{\kappa ,a}(x,y)|\le 1$
to hold. In [Reference Gorbachev, Ivanov and Tikhonov15], it was mentioned that for
$|B_{\kappa ,a}(x,y)|\le 1$
to hold. In [Reference Gorbachev, Ivanov and Tikhonov15], it was mentioned that for
![]() $a=1$
, this estimate holds also for
$a=1$
, this estimate holds also for
![]() $1/4<\kappa _0\le \kappa <1/2$
,
$1/4<\kappa _0\le \kappa <1/2$
,
![]() $\kappa _{0}\approx 0.44$
.
$\kappa _{0}\approx 0.44$
.
Note that the case
![]() $\kappa <1/2$
corresponds to
$\kappa <1/2$
corresponds to
![]() $\lambda <0$
, which we study in detail in the next section.
$\lambda <0$
, which we study in detail in the next section.
3 The case
 $d=1$
and
$d=1$
and
 $\lambda _{\kappa ,a}<0$
$\lambda _{\kappa ,a}<0$
Let us investigate whether the polynomials
![]() $q_{2r}(t,\lambda )$
and
$q_{2r}(t,\lambda )$
and
![]() $q_{2r+1}(t,\lambda )$
are nonnegative for
$q_{2r+1}(t,\lambda )$
are nonnegative for
![]() $\lambda =\lambda _{\kappa ,a}=(2\kappa -1)/a<0$
. In order to do this, we decompose them by the polynomials
$\lambda =\lambda _{\kappa ,a}=(2\kappa -1)/a<0$
. In order to do this, we decompose them by the polynomials
![]() $q_{2r}(t,0)$
and
$q_{2r}(t,0)$
and
![]() $q_{2r+1}(t,0)$
. First, we decompose the Gegenbauer polynomials in terms of the Chebyshev polynomials
$q_{2r+1}(t,0)$
. First, we decompose the Gegenbauer polynomials in terms of the Chebyshev polynomials
![]() $P_n^{(-1/2)}(\cos t)=\cos nt$
using the well-known result (see [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, 10.9(17)])
$P_n^{(-1/2)}(\cos t)=\cos nt$
using the well-known result (see [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, 10.9(17)])
 $$ \begin{align} C_{n}^{\lambda}(\cos\theta)=\sum_{s=0}^{n}\frac{(\lambda)_s(\lambda)_{n-s}}{s!\,(n-s)!}\cos{}(n-2s)\theta. \end{align} $$
$$ \begin{align} C_{n}^{\lambda}(\cos\theta)=\sum_{s=0}^{n}\frac{(\lambda)_s(\lambda)_{n-s}}{s!\,(n-s)!}\cos{}(n-2s)\theta. \end{align} $$
Let us start with the case
![]() $R=2r+1$
.
$R=2r+1$
.
Lemma 3.1. For any
![]() $r\in \mathbb {Z}_+$
and
$r\in \mathbb {Z}_+$
and
![]() $\lambda>-1/2$
, there holds
$\lambda>-1/2$
, there holds
 $$ \begin{align} P_{2r+1}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}b_s^r(\lambda)P_{2r+1-2s}^{(-1/2)}(t), \end{align} $$
$$ \begin{align} P_{2r+1}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}b_s^r(\lambda)P_{2r+1-2s}^{(-1/2)}(t), \end{align} $$
where
Proof. Taking into account (2.11) and (3.1), we obtain
 $$\begin{align*}\frac{\Gamma(2\lambda+2r+1)}{(2r+1)!\,\Gamma(2\lambda)}\,P_{2r+1}^{(\lambda-1/2)}(t)= C_{2r+1}^{\lambda}(t)=2\sum_{s=0}^{r}\frac{(\lambda)_s(\lambda)_{2r+1-s}}{s!\,(2r+1-s)!}\,P_{2r+1-2s}^{(-1/2)}(t). \end{align*}$$
$$\begin{align*}\frac{\Gamma(2\lambda+2r+1)}{(2r+1)!\,\Gamma(2\lambda)}\,P_{2r+1}^{(\lambda-1/2)}(t)= C_{2r+1}^{\lambda}(t)=2\sum_{s=0}^{r}\frac{(\lambda)_s(\lambda)_{2r+1-s}}{s!\,(2r+1-s)!}\,P_{2r+1-2s}^{(-1/2)}(t). \end{align*}$$
Hence, the duplication formula for the gamma function implies (3.3).
Remark 3.2. We see that in the decomposition (3.2), the zero coefficient is positive, and all other coefficients are also positive for
![]() $\lambda>0$
and negative for
$\lambda>0$
and negative for
![]() $\lambda <0$
. Note that the normalization of the Gegenbauer polynomials
$\lambda <0$
. Note that the normalization of the Gegenbauer polynomials
![]() $P_{n}^{(\alpha )}(1) =1$
implies the equality
$P_{n}^{(\alpha )}(1) =1$
implies the equality
 $$\begin{align*}\sum_{s=0}^{r}b_s^r(\lambda)=1 ,\end{align*}$$
$$\begin{align*}\sum_{s=0}^{r}b_s^r(\lambda)=1 ,\end{align*}$$
and for
![]() $\lambda>0$
, the Gegenbauer polynomials
$\lambda>0$
, the Gegenbauer polynomials
![]() $P_{2r+1}^{(\lambda -1/2)}(t)$
are the convex hull of the Chebyshev polynomials
$P_{2r+1}^{(\lambda -1/2)}(t)$
are the convex hull of the Chebyshev polynomials
![]() $P_{2r+1-2s}^{(-1/2)}(t)$
,
$P_{2r+1-2s}^{(-1/2)}(t)$
,
![]() $s=0,1,\dots ,r$
. In particular, one has
$s=0,1,\dots ,r$
. In particular, one has
![]() $|P_{2r+1}^{(\lambda -1/2)}(t)|\le 1$
,
$|P_{2r+1}^{(\lambda -1/2)}(t)|\le 1$
,
![]() $t\in [-1,1]$
,
$t\in [-1,1]$
,
![]() $\lambda \ge 0$
.
$\lambda \ge 0$
.
Thus, we are in a position to state the required result on the decomposition for the polynomial
![]() $q_{2r+1}(t,\lambda )$
.
$q_{2r+1}(t,\lambda )$
.
Corollary 3.3. For any
![]() $r\in \mathbb {Z}_+$
and
$r\in \mathbb {Z}_+$
and
![]() $\lambda>-1/2$
, there holds
$\lambda>-1/2$
, there holds
 $$\begin{align*}q_{2r+1}(t,\lambda)=\sum_{s=0}^{r}b_s^r(\lambda)q_{2r-2s+1}(t,0). \end{align*}$$
$$\begin{align*}q_{2r+1}(t,\lambda)=\sum_{s=0}^{r}b_s^r(\lambda)q_{2r-2s+1}(t,0). \end{align*}$$
Using (2.10) and the properties of the coefficients
![]() $b_s^r(\lambda )$
,
$b_s^r(\lambda )$
,
![]() $s=0,1,\dots ,r$
, from Remark 3.2, we establish the following result.
$s=0,1,\dots ,r$
, from Remark 3.2, we establish the following result.
Corollary 3.4. For any
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\lambda \in (-1/2,0)$
, the polynomial
$\lambda \in (-1/2,0)$
, the polynomial
![]() $q_{2r+1}(t,\lambda )$
is negative at the points of local minimum of the Chebyshev polynomial
$q_{2r+1}(t,\lambda )$
is negative at the points of local minimum of the Chebyshev polynomial
![]() $P_{2r+1}^{(-1/2)}(t)= \cos {}(({2r+1})\arccos t)$
.
$P_{2r+1}^{(-1/2)}(t)= \cos {}(({2r+1})\arccos t)$
.
In the case
![]() $R=2r$
, similarly, one can obtain the decomposition of the polynomial
$R=2r$
, similarly, one can obtain the decomposition of the polynomial
![]() $q_{2r}(t,\lambda )$
.
$q_{2r}(t,\lambda )$
.
Lemma 3.5. For any
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\lambda>-1/2$
, there holds
$\lambda>-1/2$
, there holds
 $$\begin{align*}P_{2r}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}d_s^r(\lambda)P_{2r-2s}^{(-1/2)}(t), \end{align*}$$
$$\begin{align*}P_{2r}^{(\lambda-1/2)}(t)=\sum_{s=0}^{r}d_s^r(\lambda)P_{2r-2s}^{(-1/2)}(t), \end{align*}$$
where
Proof. In light of (2.11) and (3.1), we have
 $$\begin{align*}\frac{\Gamma(2\lambda+2r)}{(2r)!\,\Gamma(2\lambda)}\,P_{2r}^{(\lambda-1/2)}(t)= C_ {2r}^{\lambda}(t)=2\sum_{s=0}^{{r-1}}\frac{(\lambda)_s(\lambda)_{2r-s}}{s!\,(2r-s)!}\,P_{2r-2s}^{(-1/2)}(t)+\frac{((\lambda)_r)^2}{(r!)^2}\,P_{0}^{(-1/2)}(t). \end{align*}$$
$$\begin{align*}\frac{\Gamma(2\lambda+2r)}{(2r)!\,\Gamma(2\lambda)}\,P_{2r}^{(\lambda-1/2)}(t)= C_ {2r}^{\lambda}(t)=2\sum_{s=0}^{{r-1}}\frac{(\lambda)_s(\lambda)_{2r-s}}{s!\,(2r-s)!}\,P_{2r-2s}^{(-1/2)}(t)+\frac{((\lambda)_r)^2}{(r!)^2}\,P_{0}^{(-1/2)}(t). \end{align*}$$
Then, using the duplication formula for gamma function, we obtain for
![]() $s=0,1,\dots ,r-1$
$s=0,1,\dots ,r-1$
while for
![]() $s=r$
,
$s=r$
,
Corollary 3.6. For any
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\lambda>-1/2$
, the following decomposition holds
$\lambda>-1/2$
, the following decomposition holds
 $$\begin{align*}q_{2r}(t,\lambda)=\sum_{s=0}^{r}d_s^r(\lambda)q_{2r-2s}(t,0). \end{align*}$$
$$\begin{align*}q_{2r}(t,\lambda)=\sum_{s=0}^{r}d_s^r(\lambda)q_{2r-2s}(t,0). \end{align*}$$
Since
![]() $ d_0^r(\lambda )>0$
and
$ d_0^r(\lambda )>0$
and
![]() ${\operatorname{sign}} d_s^r(\lambda )={\operatorname{sign}} \lambda $
,
${\operatorname{sign}} d_s^r(\lambda )={\operatorname{sign}} \lambda $
,
![]() $s=1,\dots ,r$
, for
$s=1,\dots ,r$
, for
![]() $\lambda>-1/2$
, taking into account (2.10), we arrive at the following result.
$\lambda>-1/2$
, taking into account (2.10), we arrive at the following result.
Corollary 3.7. If
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $\lambda \in (-1/2,0)$
, then the polynomial
$\lambda \in (-1/2,0)$
, then the polynomial
![]() $q_{2r}(t,\lambda )$
is negative at the points of local extremum of the Chebyshev polynomial
$q_{2r}(t,\lambda )$
is negative at the points of local extremum of the Chebyshev polynomial
![]() $P_{2r}^{(-1/2)}(t)=\cos {}(2r\arccos t)$
.
$P_{2r}^{(-1/2)}(t)=\cos {}(2r\arccos t)$
.
Corollaries 3.4 and 3.7 show that the polynomials
![]() $q_{2r}(t,\lambda )$
and
$q_{2r}(t,\lambda )$
and
![]() $q_{2r+1}(t,\lambda )$
for
$q_{2r+1}(t,\lambda )$
for
![]() $r\ge 1$
change sign and, therefore, the method of the proof of the estimate
$r\ge 1$
change sign and, therefore, the method of the proof of the estimate
![]() $|B_{\kappa ,a}(x,y)|\le 1$
used in Theorem 1.1 cannot be applied when
$|B_{\kappa ,a}(x,y)|\le 1$
used in Theorem 1.1 cannot be applied when
![]() $\lambda <0$
. In this case, the problem remains open.
$\lambda <0$
. In this case, the problem remains open.
3.1 On positive definiteness
Recall that a continuous function f on
![]() $\mathbb {R}$
is positive definite if for any
$\mathbb {R}$
is positive definite if for any
![]() $\{v_s\}_{s=1}^{n}\subset \mathbb {R}$
and
$\{v_s\}_{s=1}^{n}\subset \mathbb {R}$
and
![]() $\{z_s\}_{s=1}^{n}\subset \mathbb {C}$
there holds
$\{z_s\}_{s=1}^{n}\subset \mathbb {C}$
there holds
 $$\begin{align*}\sum_{s,l=1}^{n}z_s\overline{z_{l}}f(v_s-v_l)\ge 0. \end{align*}$$
$$\begin{align*}\sum_{s,l=1}^{n}z_s\overline{z_{l}}f(v_s-v_l)\ge 0. \end{align*}$$
Bochner’s theorem states that any continuous positive definite function
![]() $f(v)$
,
$f(v)$
,
![]() $f(0)=1$
, is the Fourier transform of a probability measure.
$f(0)=1$
, is the Fourier transform of a probability measure.
Recall that the function
![]() $e_{2r+1}(v,\lambda )$
is given in (2.4). By (2.9) and (2.10),
$e_{2r+1}(v,\lambda )$
is given in (2.4). By (2.9) and (2.10),
 $$\begin{align*}e_{2r+1}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))e^{-ivt}\,dt. \end{align*}$$
$$\begin{align*}e_{2r+1}(v,\lambda)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))e^{-ivt}\,dt. \end{align*}$$
Then, by Remark 3.2 and Corollaries 3.3 and 3.4, we deduce the following
Corollary 3.8. The function
![]() $e_{2r+1}(v,\lambda )$
is positive definite if and only if
$e_{2r+1}(v,\lambda )$
is positive definite if and only if
![]() $\lambda \ge 0$
.
$\lambda \ge 0$
.
4 The kernel of the generalized Fourier transform in the multivariate case
4.1 When the kernel is bounded by one
In this section, for the sake of completeness, we give the proof of Theorem 1.1 in the general case, following ideas from the paper [Reference Constales, De Bie and Lian10]. We stress that the proof below also allows one to deal with the case
![]() $d=1$
.
$d=1$
.
Let
![]() $d\in \mathbb {N}$
,
$d\in \mathbb {N}$
,
![]() $a>0$
,
$a>0$
,
![]() $\langle \kappa \rangle \ge 0$
, and
$\langle \kappa \rangle \ge 0$
, and
![]() $\eta =\lambda _{\kappa }=\langle \kappa \rangle +\frac {d-2}{2}>0$
. For
$\eta =\lambda _{\kappa }=\langle \kappa \rangle +\frac {d-2}{2}>0$
. For
![]() $w\ge 0$
and
$w\ge 0$
and
![]() $\tau \in [-1,1]$
, define
$\tau \in [-1,1]$
, define
 $$ \begin{align} \Psi_{a}^d(w,\tau)=2^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,w^{-2\eta/a}J_{\frac{2(\eta+j)}{a}}(w)C_{j}^{\eta}(\tau). \end{align} $$
$$ \begin{align} \Psi_{a}^d(w,\tau)=2^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,w^{-2\eta/a}J_{\frac{2(\eta+j)}{a}}(w)C_{j}^{\eta}(\tau). \end{align} $$
Putting in (4.1)
we obtain the function
 $$ \begin{align*} K_{a}^d(x,y)=a^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)(|x||y|)^{-\eta}\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,J_{\frac{2(\eta+j)}{a}}\Bigl(\frac{2}{a}(|x||y|)^{a/2}\Bigr)C_{j}^{\eta}(\langle x',\,y'\rangle). \end{align*} $$
$$ \begin{align*} K_{a}^d(x,y)=a^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)(|x||y|)^{-\eta}\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,J_{\frac{2(\eta+j)}{a}}\Bigl(\frac{2}{a}(|x||y|)^{a/2}\Bigr)C_{j}^{\eta}(\langle x',\,y'\rangle). \end{align*} $$
Note that
![]() $K_{a}^d(x,y)=K_{a}^d(y,x)$
and
$K_{a}^d(x,y)=K_{a}^d(y,x)$
and
![]() $\Psi _{a}^d(0,\tau )=K_{a}^d(0,y)=1$
.
$\Psi _{a}^d(0,\tau )=K_{a}^d(0,y)=1$
.
Let
![]() $V_{\kappa }f(x)$
be the intertwining operator in the Dunkl harmonic analysis [Reference Rösler20], which is a positive operator satisfying
$V_{\kappa }f(x)$
be the intertwining operator in the Dunkl harmonic analysis [Reference Rösler20], which is a positive operator satisfying
The representing measures
![]() $\mu _{x}^{\kappa }(\xi )$
are compactly supported probability measures with
$\mu _{x}^{\kappa }(\xi )$
are compactly supported probability measures with
![]() $\text {supp}\,\mu _{x}^{\kappa }(\xi )\subset \text {co}{}\{gx\colon g\in G\}$
[Reference Rösler22].
$\text {supp}\,\mu _{x}^{\kappa }(\xi )\subset \text {co}{}\{gx\colon g\in G\}$
[Reference Rösler22].
The kernel of the generalized Fourier transform
![]() $\mathcal {F}_{\kappa ,a}$
is given by [Reference Ben Saïd, Kobayashi and Ørsted4, Chapters 4, 5]
$\mathcal {F}_{\kappa ,a}$
is given by [Reference Ben Saïd, Kobayashi and Ørsted4, Chapters 4, 5]
 $$ \begin{align} &B_{\kappa,a}(x,y)=V_{\kappa}K_{a}^d(x,|y|\cdot)(y') \notag\\ &\qquad\quad=a^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)(|x||y|)^{-\eta}\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,J_{\frac{2(\eta+j)}{a}}\Bigl(\frac{2}{a}(|x||y|)^{a/2}\Bigr)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y'). \end{align} $$
$$ \begin{align} &B_{\kappa,a}(x,y)=V_{\kappa}K_{a}^d(x,|y|\cdot)(y') \notag\\ &\qquad\quad=a^{2\eta/a}\Gamma\Bigl(\frac{2\eta+a}{a}\Bigr)(|x||y|)^{-\eta}\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,J_{\frac{2(\eta+j)}{a}}\Bigl(\frac{2}{a}(|x||y|)^{a/2}\Bigr)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y'). \end{align} $$
If
![]() $\langle \kappa \rangle =0$
, that is,
$\langle \kappa \rangle =0$
, that is,
![]() $\eta =(d-2)/2$
, then
$\eta =(d-2)/2$
, then
![]() $V_{\kappa }=\text {I}$
is the identity operator and
$V_{\kappa }=\text {I}$
is the identity operator and
![]() $K_{a}^d(x,y)=B_{0,a}(x,y)$
.
$K_{a}^d(x,y)=B_{0,a}(x,y)$
.
Since the operator
![]() $V_{\kappa }$
is positive and
$V_{\kappa }$
is positive and
![]() $V_{\kappa }1=1$
, the proof of equality (1.2) can proceed as follows: If
$V_{\kappa }1=1$
, the proof of equality (1.2) can proceed as follows: If
![]() $|\Psi _{a}^d(w,\tau )|\le 1$
, then
$|\Psi _{a}^d(w,\tau )|\le 1$
, then
![]() $|B_{\kappa ,a}(x,y)|\le 1$
.
$|B_{\kappa ,a}(x,y)|\le 1$
.
Let further
![]() $\frac {2}{a}\in \mathbb {N}$
,
$\frac {2}{a}\in \mathbb {N}$
,
![]() $a=\frac {2}{R}$
. The inequality
$a=\frac {2}{R}$
. The inequality
![]() $|\Psi _{a}^d(w,\tau )|\le 1$
was proved in [Reference Constales, De Bie and Lian10] under the conditions
$|\Psi _{a}^d(w,\tau )|\le 1$
was proved in [Reference Constales, De Bie and Lian10] under the conditions
![]() $\eta>0$
and
$\eta>0$
and
![]() $\eta =(d-2)/2$
. We note that the proof of this estimate in [Reference Constales, De Bie and Lian10] also holds for
$\eta =(d-2)/2$
. We note that the proof of this estimate in [Reference Constales, De Bie and Lian10] also holds for
![]() $\eta =\langle \kappa \rangle +(d-2)/2>0$
. Hence, (1.2) is valid for
$\eta =\langle \kappa \rangle +(d-2)/2>0$
. Hence, (1.2) is valid for
![]() $\langle \kappa \rangle +(d-2)/2>0$
. If
$\langle \kappa \rangle +(d-2)/2>0$
. If
![]() $\eta =0$
, then
$\eta =0$
, then
![]() $d=1$
,
$d=1$
,
![]() $\kappa =1/2$
or
$\kappa =1/2$
or
![]() $d=2$
,
$d=2$
,
![]() $\kappa \equiv 0$
, and in these cases, (1.2) holds as well (see Theorem 1.1 and [Reference De Bie5]). This completes the proof of Theorem 1.1.
$\kappa \equiv 0$
, and in these cases, (1.2) holds as well (see Theorem 1.1 and [Reference De Bie5]). This completes the proof of Theorem 1.1.
4.2 Positive definiteness of
 $\Psi _{a}^d$
. Another proof of Theorem 1.1
$\Psi _{a}^d$
. Another proof of Theorem 1.1
In [Reference Constales, De Bie and Lian10], to evaluate the kernel
![]() $B_{0,a}(x,y)$
, the authors used the Laplace transform of the function
$B_{0,a}(x,y)$
, the authors used the Laplace transform of the function
![]() $\Psi _{a}^d$
given by (4.1). In the general case
$\Psi _{a}^d$
given by (4.1). In the general case
![]() $d\ge 1$
, we give another proof of the estimate
$d\ge 1$
, we give another proof of the estimate
![]() $|\Psi _{a}^d|\le 1$
based on the approach from the papers [Reference De Bie and Lian6, Reference Deleaval and Demni11], which allows one to show positive definiteness of the function
$|\Psi _{a}^d|\le 1$
based on the approach from the papers [Reference De Bie and Lian6, Reference Deleaval and Demni11], which allows one to show positive definiteness of the function
![]() $\Psi _{a}^d(w,\tau )$
with respect to w. Note also that for
$\Psi _{a}^d(w,\tau )$
with respect to w. Note also that for
![]() $a=1,2$
, the functions
$a=1,2$
, the functions
are positive definite (see [Reference Ben Saïd, Kobayashi and Ørsted4, Example 4.18], [Reference Constales, De Bie and Lian10]).
Let
 $$\begin{align*}I_{\eta}(b)=\Bigl(\frac{b}{2}\Bigr)^{\eta}\,\sum_{j=0}^{\infty}\frac{1}{j!\,\Gamma(j+\eta+1)}\Bigl(\frac{b^2}{4}\Bigr)^j \end{align*}$$
$$\begin{align*}I_{\eta}(b)=\Bigl(\frac{b}{2}\Bigr)^{\eta}\,\sum_{j=0}^{\infty}\frac{1}{j!\,\Gamma(j+\eta+1)}\Bigl(\frac{b^2}{4}\Bigr)^j \end{align*}$$
be the modified Bessel function of the first kind (see [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter 7, 7.2.2]) and
 $$\begin{align*}\Phi_2^{(m)}(\beta_1,\dots,\beta_m;\gamma;x_1,\dots,x_m)= \sum_{j_1,\dots,j_m\ge 0}\frac{(\beta_1)_{j_1}\cdots (\beta_m)_{j_m}}{(\gamma)_{j_1+\cdots+j_m}}\,\frac{x_1^{j_1}}{j_{1}!}\cdots\frac{x_m^{j_m}}{j_{m}!} \end{align*}$$
$$\begin{align*}\Phi_2^{(m)}(\beta_1,\dots,\beta_m;\gamma;x_1,\dots,x_m)= \sum_{j_1,\dots,j_m\ge 0}\frac{(\beta_1)_{j_1}\cdots (\beta_m)_{j_m}}{(\gamma)_{j_1+\cdots+j_m}}\,\frac{x_1^{j_1}}{j_{1}!}\cdots\frac{x_m^{j_m}}{j_{m}!} \end{align*}$$
be the second Humbert function of m variables (see [Reference Exton14, Chapter 2, 2.1.1.2]). In the case when
![]() $\gamma -\sum _{j=1}^m\beta _j>0$
and
$\gamma -\sum _{j=1}^m\beta _j>0$
and
![]() $\beta _j>0$
,
$\beta _j>0$
,
![]() $j=1,\dots ,m$
, the hypergeometric function
$j=1,\dots ,m$
, the hypergeometric function
![]() $\Phi _2^{(m)}$
admits the following integral representation
$\Phi _2^{(m)}$
admits the following integral representation
 $$ \begin{align} \Phi_2^{(m)}(\beta_1,\dots,\beta_m;\gamma;x_1,\dots,x_m) =C_{\beta}^{(\gamma)}\int_{T^m}e^{\sum_{j=1}^mx_jt_j}\Bigl(1-\sum_{j=1}^{m}t_j\Bigr)^{\gamma-\sum_{j=1}^m\beta_j-1} \prod_{j=1}^{m}t_j^{\beta_j-1}\,dt_1\cdots dt_m, \end{align} $$
$$ \begin{align} \Phi_2^{(m)}(\beta_1,\dots,\beta_m;\gamma;x_1,\dots,x_m) =C_{\beta}^{(\gamma)}\int_{T^m}e^{\sum_{j=1}^mx_jt_j}\Bigl(1-\sum_{j=1}^{m}t_j\Bigr)^{\gamma-\sum_{j=1}^m\beta_j-1} \prod_{j=1}^{m}t_j^{\beta_j-1}\,dt_1\cdots dt_m, \end{align} $$
where
 $$\begin{align*}C_{\beta}^{(\gamma)}=\frac{\Gamma(\gamma)}{\Gamma(\gamma-\sum_{j=1}^{m}\beta_j)\prod_{j=1}^{m}\Gamma(\beta_j)} \end{align*}$$
$$\begin{align*}C_{\beta}^{(\gamma)}=\frac{\Gamma(\gamma)}{\Gamma(\gamma-\sum_{j=1}^{m}\beta_j)\prod_{j=1}^{m}\Gamma(\beta_j)} \end{align*}$$
and
 $$\begin{align*}T^m=\Bigl\{(t_1,\dots,t_m)\colon t_j\ge 0,\ j=1,\dots,m,\ \sum_{j=1}^{m}t_j\le 1\Bigr\} \end{align*}$$
$$\begin{align*}T^m=\Bigl\{(t_1,\dots,t_m)\colon t_j\ge 0,\ j=1,\dots,m,\ \sum_{j=1}^{m}t_j\le 1\Bigr\} \end{align*}$$
is the unit simplex in
![]() $\mathbb {R}^m$
([Reference Chamayou and Wesolowski9, Reference Humbert17]).
$\mathbb {R}^m$
([Reference Chamayou and Wesolowski9, Reference Humbert17]).
Taking into account the results from [Reference De Bie and Lian6, Reference Deleaval and Demni11], we obtain the following proposition, which gives an alternative proof of Theorem 1.1.
Proposition 4.1. Let
![]() $d\in \mathbb {N}$
,
$d\in \mathbb {N}$
,
![]() $a=\frac {2}{R}$
,
$a=\frac {2}{R}$
,
![]() $R\in \mathbb {N}$
,
$R\in \mathbb {N}$
,
![]() $R\ge 2$
,
$R\ge 2$
,
![]() $\eta =\langle \kappa \rangle +\frac {d-2}{2}>0$
,
$\eta =\langle \kappa \rangle +\frac {d-2}{2}>0$
,
![]() $\tau \in [-1,1]$
, and
$\tau \in [-1,1]$
, and
![]() $q=\arccos \tau $
. The function
$q=\arccos \tau $
. The function
![]() $w \mapsto \Psi _{a}^d(w,\tau )$
is a positive definite entire function of exponential type
$w \mapsto \Psi _{a}^d(w,\tau )$
is a positive definite entire function of exponential type
 $$ \begin{align} \theta(a,\tau)= \begin{cases} \cos\frac{q}{R}, & R=2r\ \text{and}\ 0\le q\le\pi \ \text{or}\ R=2r+1\ \text{and}\ 0\le q\le\pi/2,\\ \cos\frac{\pi-q}{R}, & R=2r+1\ \text{and}\ \pi/2\le q\le\pi. \end{cases} \end{align} $$
$$ \begin{align} \theta(a,\tau)= \begin{cases} \cos\frac{q}{R}, & R=2r\ \text{and}\ 0\le q\le\pi \ \text{or}\ R=2r+1\ \text{and}\ 0\le q\le\pi/2,\\ \cos\frac{\pi-q}{R}, & R=2r+1\ \text{and}\ \pi/2\le q\le\pi. \end{cases} \end{align} $$
Proof. Let us consider the function
 $$\begin{align*}f_{R,\eta}(b,\tau)=\Gamma(R\eta+1)\Bigl(\frac{b}{2}\Bigr)^{\eta}\sum_{j=0}^{\infty} \frac{j+\eta}{\eta}\,I_{R(j+\eta)}(b)C_{j}^{\eta}(\tau), \quad R\in\mathbb{N}. \end{align*}$$
$$\begin{align*}f_{R,\eta}(b,\tau)=\Gamma(R\eta+1)\Bigl(\frac{b}{2}\Bigr)^{\eta}\sum_{j=0}^{\infty} \frac{j+\eta}{\eta}\,I_{R(j+\eta)}(b)C_{j}^{\eta}(\tau), \quad R\in\mathbb{N}. \end{align*}$$
Let
![]() $\tau =\langle x',\,y'\rangle $
,
$\tau =\langle x',\,y'\rangle $
,
![]() $b=-iw$
,
$b=-iw$
,
![]() $R=\frac {2}{a}$
,
$R=\frac {2}{a}$
,
![]() $R\ge 2$
. Since
$R\ge 2$
. Since
![]() $I_{\eta }(-iw)=e^{-i\frac {\pi \eta }{2}}J_{\eta }(w)$
[Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter 7, 7.2.2], then
$I_{\eta }(-iw)=e^{-i\frac {\pi \eta }{2}}J_{\eta }(w)$
[Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter 7, 7.2.2], then
![]() $f_{R,\eta }(b,\tau )=\Psi _{a}^d(w,\tau )$
. It is known (see [Reference De Bie and Lian6, Reference Deleaval and Demni11]) that
$f_{R,\eta }(b,\tau )=\Psi _{a}^d(w,\tau )$
. It is known (see [Reference De Bie and Lian6, Reference Deleaval and Demni11]) that
where
![]() $b_j=b\cos {}(\frac {q-2\pi j}{R})$
,
$b_j=b\cos {}(\frac {q-2\pi j}{R})$
,
![]() $j=0,\dots ,R-1$
. In light of (4.4) and using
$j=0,\dots ,R-1$
. In light of (4.4) and using
![]() $\eta>0$
, we get
$\eta>0$
, we get
 $$ \begin{align} &\Psi_{a}^d(w,\tau)=f_{R,\eta}(-iw,\tau)\notag\\ &\qquad=C_{\eta}\int_{T^{R-1}}e^{-iw\{\cos{}(\frac{q}{R})+\sum_{j=1}^{R-1}(\cos{}(\frac{q-2\pi j}{R})-\cos{}(\frac{q}{R}))t_j\}}\Bigl(1-\sum_{j=1}^{R-1}t_j\Bigr)^{\eta-1}\prod_{j=1}^{R-1}t_j^{\eta-1}\, \,dt_1\cdots dt_{R-1}, \end{align} $$
$$ \begin{align} &\Psi_{a}^d(w,\tau)=f_{R,\eta}(-iw,\tau)\notag\\ &\qquad=C_{\eta}\int_{T^{R-1}}e^{-iw\{\cos{}(\frac{q}{R})+\sum_{j=1}^{R-1}(\cos{}(\frac{q-2\pi j}{R})-\cos{}(\frac{q}{R}))t_j\}}\Bigl(1-\sum_{j=1}^{R-1}t_j\Bigr)^{\eta-1}\prod_{j=1}^{R-1}t_j^{\eta-1}\, \,dt_1\cdots dt_{R-1}, \end{align} $$
where
![]() $C_{\eta }=\Gamma (R\eta )/(\Gamma (\eta ))^R$
. For
$C_{\eta }=\Gamma (R\eta )/(\Gamma (\eta ))^R$
. For
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $\beta \in \mathbb {R}$
, the function
$\beta \in \mathbb {R}$
, the function
![]() $\alpha e^{i\beta w}$
is positive definite, hence the function
$\alpha e^{i\beta w}$
is positive definite, hence the function
![]() $\Psi _{a}^d(w,\tau )$
is also positive definite with respect to w.
$\Psi _{a}^d(w,\tau )$
is also positive definite with respect to w.
The representation (4.6) implies that
![]() $\Psi _a^d(w,\tau )$
is an entire function of exponential type with respect to w. Let us calculate its type. Since for
$\Psi _a^d(w,\tau )$
is an entire function of exponential type with respect to w. Let us calculate its type. Since for
![]() $j=1,\dots ,R-1$
,
$j=1,\dots ,R-1$
,
![]() $q=\arccos \tau $
,
$q=\arccos \tau $
,
![]() $\tau \in [-1,1]$
,
$\tau \in [-1,1]$
,
![]() $ \cos \frac {q}{R}-\cos \frac {q-2\pi j}{R}=2\sin \frac {\pi i}{R}\,\sin \frac {\pi j-q}{R}\ge 0, $
then for any
$ \cos \frac {q}{R}-\cos \frac {q-2\pi j}{R}=2\sin \frac {\pi i}{R}\,\sin \frac {\pi j-q}{R}\ge 0, $
then for any
![]() $(t_1,\dots ,t_{R-1})\in T^{R-1}$
,
$(t_1,\dots ,t_{R-1})\in T^{R-1}$
,
 $$\begin{align*}\min_{1\le j\le R-1}\cos\frac{q-2\pi j}{R}\le \cos\frac{q}{R}+\sum_{j=1}^{R-1}\Bigl(\cos\frac{q-2\pi j}{R}-\cos\frac{q}{R}\Bigr)t_j\le \cos\frac{q}{R}. \end{align*}$$
$$\begin{align*}\min_{1\le j\le R-1}\cos\frac{q-2\pi j}{R}\le \cos\frac{q}{R}+\sum_{j=1}^{R-1}\Bigl(\cos\frac{q-2\pi j}{R}-\cos\frac{q}{R}\Bigr)t_j\le \cos\frac{q}{R}. \end{align*}$$
Since
 $$ \begin{align*} \min_{1\le j\le R-1}\cos\frac{q-2\pi j}{R}= \begin{cases}-\cos\frac{q}{R}, & R=2r\ \text{or}\ R=2r+1\ \text{and}\ 0\le q\le\pi/2,\\ -\cos\frac{\pi-q}{R}, & R=2r+1\ \text{and}\ \pi/2\le q\le\pi, \end{cases} \end{align*} $$
$$ \begin{align*} \min_{1\le j\le R-1}\cos\frac{q-2\pi j}{R}= \begin{cases}-\cos\frac{q}{R}, & R=2r\ \text{or}\ R=2r+1\ \text{and}\ 0\le q\le\pi/2,\\ -\cos\frac{\pi-q}{R}, & R=2r+1\ \text{and}\ \pi/2\le q\le\pi, \end{cases} \end{align*} $$
the type of the function
![]() $\Psi _{a}^d(w,\tau )$
is given by (4.5).
$\Psi _{a}^d(w,\tau )$
is given by (4.5).
Remark 4.2. Let
![]() $t,\tau \in (-1,1)$
,
$t,\tau \in (-1,1)$
,
![]() $\lambda =2\eta /a$
,
$\lambda =2\eta /a$
,
![]() $a=1/r$
,
$a=1/r$
,
![]() $r\in \mathbb {N}$
. Then the function
$r\in \mathbb {N}$
. Then the function
![]() $\Psi _{a}^{d}(w,\tau )$
has the following integral representation
$\Psi _{a}^{d}(w,\tau )$
has the following integral representation
 $$ \begin{align} \Psi_{a}^{d}(w,\tau)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2j/a}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)e^{-iwt}\,dt. \end{align} $$
$$ \begin{align} \Psi_{a}^{d}(w,\tau)=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2j/a}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)e^{-iwt}\,dt. \end{align} $$
Indeed, using (2.8) and (4.1) and Lemmas 2.2 and 2.6, we get
 $$ \begin{align*} &\Psi_{a}^d(w,\tau)=\sum_{j=0}^{\infty}(-1)^{rj}\,\frac{\eta+j}{\eta}\,\frac{w^{2rj}}{2^{2rj}(\lambda+1)_{2rj}}\,j_{\lambda+2rj}(w) C_{j}^{\eta}(\tau)\\ &=\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\Bigl\{j_{\lambda}(w)+\sum_{s=1}^{rj-1}(-1)^s\binom{rj}{s}\frac{(\lambda+rj)_s}{(\lambda+1)_s}\,j_{\lambda+s}(w) {+}(-1)^{rj}\,\frac{(\lambda+rj+1)_{rj-1}}{(\lambda+1)_{rj-1}}\,j_{\lambda+rj}(w)\Bigr\}C_{j}^{\eta}(\tau)\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2rj}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)e^{-iwt}\,dt. \end{align*} $$
$$ \begin{align*} &\Psi_{a}^d(w,\tau)=\sum_{j=0}^{\infty}(-1)^{rj}\,\frac{\eta+j}{\eta}\,\frac{w^{2rj}}{2^{2rj}(\lambda+1)_{2rj}}\,j_{\lambda+2rj}(w) C_{j}^{\eta}(\tau)\\ &=\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\Bigl\{j_{\lambda}(w)+\sum_{s=1}^{rj-1}(-1)^s\binom{rj}{s}\frac{(\lambda+rj)_s}{(\lambda+1)_s}\,j_{\lambda+s}(w) {+}(-1)^{rj}\,\frac{(\lambda+rj+1)_{rj-1}}{(\lambda+1)_{rj-1}}\,j_{\lambda+rj}(w)\Bigr\}C_{j}^{\eta}(\tau)\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad=c_{\lambda}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2rj}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)e^{-iwt}\,dt. \end{align*} $$
The integral representation (4.7) implies that
 $$ \begin{align*} \psi_a^d(t,\tau)=\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2rj}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)\ge 0,\quad t,\,\tau\in (-1,1), \end{align*} $$
$$ \begin{align*} \psi_a^d(t,\tau)=\sum_{j=0}^{\infty}\frac{\eta+j}{\eta}\,P_{2rj}^{(\lambda-1/2)}(t) C_{j}^{\eta}(\tau)\ge 0,\quad t,\,\tau\in (-1,1), \end{align*} $$
is equivalent to the positive definiteness of the function
![]() $\Psi _{a}^d(w,\tau )$
. Proposition 4.1 shows that the function
$\Psi _{a}^d(w,\tau )$
. Proposition 4.1 shows that the function
![]() $\psi _{a}^d(t,\tau )$
is positive and its support as a function of t lies on the interval
$\psi _{a}^d(t,\tau )$
is positive and its support as a function of t lies on the interval
![]() $I_a=[-\theta (a,\tau ),\theta (a,\tau )]$
.
$I_a=[-\theta (a,\tau ),\theta (a,\tau )]$
.
In the case
![]() $a=1$
, one can easily write an explicit formula for
$a=1$
, one can easily write an explicit formula for
![]() $\psi _{1}^d(t,\tau )$
. In more detail, we have
$\psi _{1}^d(t,\tau )$
. In more detail, we have
![]() $r=1$
,
$r=1$
,
![]() $\lambda =2\eta $
, and
$\lambda =2\eta $
, and
![]() $\theta (a,\tau )=\cos \frac {q}{2}=\sqrt {(1+\tau )/2}$
. Then using [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi2, Chapter VIII, 8.7(31)], we obtain
$\theta (a,\tau )=\cos \frac {q}{2}=\sqrt {(1+\tau )/2}$
. Then using [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi2, Chapter VIII, 8.7(31)], we obtain
 $$ \begin{align*} \psi_{1}^d(t,\tau)&=(2\pi c_{\lambda})^{-1}(1-t^2)^{1/2-2\eta}\int_{-\infty}^{\infty}j_{\eta-1/2}(w\sqrt{(1+\tau)/2})e^{iwt}\,dw\\ &=c(\eta)(1-t^2)^{1/2-2\eta}(1+\tau)^{1/2-\eta}(1+\tau-2t^2)^{\eta-1}\chi_{I_1}(t)\\ &=c(\eta)(1-t^2)^{1/2-2\eta}(1+\tau)^{1/2-\eta}(\tau-P_2^{(-1/2)}(t))^{\eta-1}\chi_{I_1}(t), \end{align*} $$
$$ \begin{align*} \psi_{1}^d(t,\tau)&=(2\pi c_{\lambda})^{-1}(1-t^2)^{1/2-2\eta}\int_{-\infty}^{\infty}j_{\eta-1/2}(w\sqrt{(1+\tau)/2})e^{iwt}\,dw\\ &=c(\eta)(1-t^2)^{1/2-2\eta}(1+\tau)^{1/2-\eta}(1+\tau-2t^2)^{\eta-1}\chi_{I_1}(t)\\ &=c(\eta)(1-t^2)^{1/2-2\eta}(1+\tau)^{1/2-\eta}(\tau-P_2^{(-1/2)}(t))^{\eta-1}\chi_{I_1}(t), \end{align*} $$
where
![]() $\chi _{I_1}(t)$
is the characteristic function of the interval
$\chi _{I_1}(t)$
is the characteristic function of the interval
![]() $I_1$
and
$I_1$
and
![]() $P_2^{(-1/2)}(t)= \cos {}(2\arccos t)$
.
$P_2^{(-1/2)}(t)= \cos {}(2\arccos t)$
.
4.3 Parameters when the kernel is not bounded by one
We will show that in some cases the uniform norm of the kernel
![]() $B_{\kappa ,a}(x,y)$
is not bounded by
$B_{\kappa ,a}(x,y)$
is not bounded by
![]() $1$
and can be either finite or infinite. We mention that the conditions when the norm is not finite are known only in the one-dimensional case. In particular, if
$1$
and can be either finite or infinite. We mention that the conditions when the norm is not finite are known only in the one-dimensional case. In particular, if
![]() $d=1$
,
$d=1$
,
![]() $0<a<2$
, and
$0<a<2$
, and
![]() $\kappa <\frac {1}{2}-\frac {a}{4}$
, then
$\kappa <\frac {1}{2}-\frac {a}{4}$
, then
![]() $\|B_{\kappa ,a}\|_{\infty }=\infty $
(see Proposition 2.1).
$\|B_{\kappa ,a}\|_{\infty }=\infty $
(see Proposition 2.1).
Proof of Theorem 1.2.
Let first
![]() $d=1$
and
$d=1$
and
![]() $\lambda =\lambda _{\kappa ,a}=\frac {2\kappa -1}{a}$
. Changing variables
$\lambda =\lambda _{\kappa ,a}=\frac {2\kappa -1}{a}$
. Changing variables
![]() $x=(\frac {a}{2}|v|)^{2/a}{\operatorname{sign}}\ {}v$
in (2.3), we get
$x=(\frac {a}{2}|v|)^{2/a}{\operatorname{sign}}\ {}v$
in (2.3), we get
 $$ \begin{align} e_{\kappa,a}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{a}{2}\,|v|\Bigr)^{2/a}{\operatorname{sign}}{}\ v\Bigr) =j_{\lambda}(v)&+\frac{\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\, |v|^{2/a}j_{\lambda+\frac{2}{a}}(v){\operatorname{sign}}{}\ v\notag\\ &{}-i\,\frac{\Gamma(\lambda+1)\sin\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\, |v|^{2/a}j_{\lambda+\frac{2}{a}}(v){\operatorname{sign}}{}\ v. \end{align} $$
$$ \begin{align} e_{\kappa,a}(v,\lambda)=b_{\kappa,a}\Bigl(\Bigl(\frac{a}{2}\,|v|\Bigr)^{2/a}{\operatorname{sign}}{}\ v\Bigr) =j_{\lambda}(v)&+\frac{\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\, |v|^{2/a}j_{\lambda+\frac{2}{a}}(v){\operatorname{sign}}{}\ v\notag\\ &{}-i\,\frac{\Gamma(\lambda+1)\sin\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\, |v|^{2/a}j_{\lambda+\frac{2}{a}}(v){\operatorname{sign}}{}\ v. \end{align} $$
If
![]() $0<a\le 1$
and
$0<a\le 1$
and
![]() $\kappa =\frac {1}{2}-\frac {a}{4}$
, then
$\kappa =\frac {1}{2}-\frac {a}{4}$
, then
![]() $\lambda =-1/2$
,
$\lambda =-1/2$
,
![]() $j_{-1/2}(v)=\cos v$
,
$j_{-1/2}(v)=\cos v$
,
![]() $j_{1/2}(v)=\frac {\sin v}{v}$
.
$j_{1/2}(v)=\frac {\sin v}{v}$
.
Assume first that
![]() $\cos \frac {\pi }{a}=0$
or
$\cos \frac {\pi }{a}=0$
or
![]() $a=\frac {2}{2r+1}$
,
$a=\frac {2}{2r+1}$
,
![]() $r\in \mathbb {N}$
. Since
$r\in \mathbb {N}$
. Since
![]() $\sin \frac {\pi }{a}\neq 0$
,
$\sin \frac {\pi }{a}\neq 0$
,
![]() $j_{-1/2}(2\pi )=1$
,
$j_{-1/2}(2\pi )=1$
,
![]() ${j_{1/2}(2\pi )=0}$
, and
${j_{1/2}(2\pi )=0}$
, and
![]() $j_{2r+1/2}(2\pi )\neq 0$
(see [Reference Watson25, Chapter 15, 15.28]), then from (4.8), we get
$j_{2r+1/2}(2\pi )\neq 0$
(see [Reference Watson25, Chapter 15, 15.28]), then from (4.8), we get
![]() $|e_{\kappa ,a}(2\pi ,-1/2)|=|e_{2r+1}(2\pi ,-1/2)|>1$
.
$|e_{\kappa ,a}(2\pi ,-1/2)|=|e_{2r+1}(2\pi ,-1/2)|>1$
.
Let now
![]() $\cos {}(\pi /a)\neq 0$
. In light of (4.8), there holds
$\cos {}(\pi /a)\neq 0$
. In light of (4.8), there holds
 $$\begin{align*}|e_{\kappa,a}(v,\lambda)|\ge \Bigl|\cos v+\frac{\Gamma(\frac{1}{2})\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\frac{2}{a}+\frac{1}{2})}\, |v|^{2/a}j_{\frac{2}{a}-\frac{1}{2}}(v){\operatorname{sign}}{}\ v\Bigr|. \end{align*}$$
$$\begin{align*}|e_{\kappa,a}(v,\lambda)|\ge \Bigl|\cos v+\frac{\Gamma(\frac{1}{2})\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\frac{2}{a}+\frac{1}{2})}\, |v|^{2/a}j_{\frac{2}{a}-\frac{1}{2}}(v){\operatorname{sign}}{}\ v\Bigr|. \end{align*}$$
Since
 $$\begin{align*}(2\pi s)^{2/a}j_{\frac{2}{a}-\frac{1}{2}}(2\pi s)=\frac{2^{2/a}\Gamma(\frac{2}{a}+\frac{1}{2})}{\Gamma(\frac{1}{2})}\, \Bigl\{\cos\frac{\pi}{a}+O\Bigl(\frac{1}{s}\Bigr)\Bigr\} \end{align*}$$
$$\begin{align*}(2\pi s)^{2/a}j_{\frac{2}{a}-\frac{1}{2}}(2\pi s)=\frac{2^{2/a}\Gamma(\frac{2}{a}+\frac{1}{2})}{\Gamma(\frac{1}{2})}\, \Bigl\{\cos\frac{\pi}{a}+O\Bigl(\frac{1}{s}\Bigr)\Bigr\} \end{align*}$$
as
![]() $s\to +\infty $
(see [Reference Watson25, Chapter VII, 7.1]), we deduce that for sufficiently large s
$s\to +\infty $
(see [Reference Watson25, Chapter VII, 7.1]), we deduce that for sufficiently large s
which completes the proof of (1.3). Note that similar arguments also imply the proof of (1.3) for
![]() $1<a<2$
and
$1<a<2$
and
![]() $\kappa =\frac {1}{2}-\frac {a}{4}$
.
$\kappa =\frac {1}{2}-\frac {a}{4}$
.
Now, we consider the multivariate case. Suppose that
![]() $d\ge 1$
,
$d\ge 1$
,
![]() $a\in (1,2)\cup (2,\infty )$
,
$a\in (1,2)\cup (2,\infty )$
,
![]() $\langle \kappa \rangle \ge 0$
, and
$\langle \kappa \rangle \ge 0$
, and
![]() $\eta =\lambda _{\kappa }$
,
$\eta =\lambda _{\kappa }$
,
![]() $\lambda =\frac {2\eta }{a}=\frac {2\langle \kappa \rangle +d-2}{a}$
. Recall that
$\lambda =\frac {2\eta }{a}=\frac {2\langle \kappa \rangle +d-2}{a}$
. Recall that
![]() $x'$
,
$x'$
,
![]() $y'$
, w are defined in (4.2). In view of (2.2) and the proof for the case
$y'$
, w are defined in (4.2). In view of (2.2) and the proof for the case
![]() $d=1$
, we may assume that
$d=1$
, we may assume that
![]() $\eta ,\lambda>-1/2$
and
$\eta ,\lambda>-1/2$
and
![]() $\cos \frac {\pi }{a}\neq 0$
.
$\cos \frac {\pi }{a}\neq 0$
.
Note that (4.3) can be equivalently written as
 $$\begin{align*}B_{\kappa,a}(x,y) =\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,\frac{\Gamma(\lambda+1)}{2^{2j/a}\,\Gamma(\lambda+1+2j/a)}\,w^{2j/a} j_{\lambda+\frac{2j}{a}}(w)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y'). \end{align*}$$
$$\begin{align*}B_{\kappa,a}(x,y) =\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,\frac{\Gamma(\lambda+1)}{2^{2j/a}\,\Gamma(\lambda+1+2j/a)}\,w^{2j/a} j_{\lambda+\frac{2j}{a}}(w)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y'). \end{align*}$$
For Gegenbauer polynomials (2.11), the following estimate holds
[Reference Ben Saïd, Kobayashi and Ørsted4, Lemma 4.9]. Using (2.11), we get
Since
![]() $|j_{\lambda }(w)|\le 1$
,
$|j_{\lambda }(w)|\le 1$
,
![]() $\frac {1}{\eta }\,C_1^{\eta }(t)=2t$
, then for
$\frac {1}{\eta }\,C_1^{\eta }(t)=2t$
, then for
![]() $0\le w\le 1$
, we have
$0\le w\le 1$
, we have
 $$ \begin{align*} \Bigl|\sum_{j=2}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,\frac{\Gamma(\lambda+1)}{2^{2j/a}\Gamma(\lambda+1+2j/a)}\,w^{2j/a} &j_{\lambda+\frac{2j}{a}}(w)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y')\Bigr|\\ &{}\le c(\eta)w^{4/a}\sum_{j=2}^{\infty}\frac{\Gamma(\lambda+1)(j^{2\eta}+1)}{2^{2j/a}\Gamma(\lambda+1+2j/a)} \le c(a,\kappa)w^{4/a} \end{align*} $$
$$ \begin{align*} \Bigl|\sum_{j=2}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\eta+j}{\eta}\,\frac{\Gamma(\lambda+1)}{2^{2j/a}\Gamma(\lambda+1+2j/a)}\,w^{2j/a} &j_{\lambda+\frac{2j}{a}}(w)V_{\kappa}C_{j}^{\eta}(\langle x',{\cdot}\,\rangle)(y')\Bigr|\\ &{}\le c(\eta)w^{4/a}\sum_{j=2}^{\infty}\frac{\Gamma(\lambda+1)(j^{2\eta}+1)}{2^{2j/a}\Gamma(\lambda+1+2j/a)} \le c(a,\kappa)w^{4/a} \end{align*} $$
and
 $$ \begin{align*} B_{\kappa,a}(x,y)=j_{\lambda}(w)&+\frac{2(\eta+1)\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')\\ &{}-i\,\frac{2(\eta+1)\Gamma(\lambda+1)\sin\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')+O(w^{4/a}),\quad w\to 0. \end{align*} $$
$$ \begin{align*} B_{\kappa,a}(x,y)=j_{\lambda}(w)&+\frac{2(\eta+1)\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')\\ &{}-i\,\frac{2(\eta+1)\Gamma(\lambda+1)\sin\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')+O(w^{4/a}),\quad w\to 0. \end{align*} $$
Therefore,
 $$ \begin{align} |B_{\kappa,a}(x,y)|\ge \Bigl|j_{\lambda}(w)+\frac{2(\eta+1)\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')+O(w^{4/a})\Bigr|. \end{align} $$
$$ \begin{align} |B_{\kappa,a}(x,y)|\ge \Bigl|j_{\lambda}(w)+\frac{2(\eta+1)\Gamma(\lambda+1)\cos\frac{\pi}{a}}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} j_{\lambda+\frac{2}{a}}(w)V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')+O(w^{4/a})\Bigr|. \end{align} $$
Since the operator
![]() $V_{\kappa }$
is an isomorphism on the space of homogeneous polynomials of degree
$V_{\kappa }$
is an isomorphism on the space of homogeneous polynomials of degree
![]() $1$
, then for suitable
$1$
, then for suitable
![]() $x',y'\in \mathbb {S}^{d-1}$
, we deduce
$x',y'\in \mathbb {S}^{d-1}$
, we deduce
We have
as
![]() $w\to 0$
. This, (4.9) and (4.10) imply that, for given
$w\to 0$
. This, (4.9) and (4.10) imply that, for given
![]() $x',y'\in \mathbb {S}^{d-1}$
as above and sufficiently small positive w,
$x',y'\in \mathbb {S}^{d-1}$
as above and sufficiently small positive w,
 $$\begin{align*}|B_{\kappa,a}(x,y)|\ge 1+\frac{2(\eta+1)\Gamma(\lambda+1)|\!\cos\frac{\pi}{a}|}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} |V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')|+O(w^{4/a})+O(w^2)>1.\\[-42pt] \end{align*}$$
$$\begin{align*}|B_{\kappa,a}(x,y)|\ge 1+\frac{2(\eta+1)\Gamma(\lambda+1)|\!\cos\frac{\pi}{a}|}{2^{2/a}\Gamma(\lambda+1+2/a)}\,w^{2/a} |V_{\kappa}(\langle x',{\cdot}\,\rangle)(y')|+O(w^{4/a})+O(w^2)>1.\\[-42pt] \end{align*}$$
Remark 4.3.
-
(i) For
 $0<a\le 1$
,
$0<a\le 1$
,
 $\frac {2}{a}\in \mathbb {N}$
, equality (1.2) holds provided
$\frac {2}{a}\in \mathbb {N}$
, equality (1.2) holds provided
 $\kappa \ge \kappa _0(a)$
, where
$\kappa \ge \kappa _0(a)$
, where
 $\frac {1}{2}-\frac {a}{4}<\kappa _0(a)\le 1/2$
. The problem of determining
$\frac {1}{2}-\frac {a}{4}<\kappa _0(a)\le 1/2$
. The problem of determining
 $\kappa _0(a)$
is open.
$\kappa _0(a)$
is open. -
(ii) Theorem 1.2 shows that our conjecture in [Reference Gorbachev, Ivanov and Tikhonov15] asserting that (1.3) holds under the condition
 $2\langle \kappa \rangle +d+a\ge 3$
is not valid for
$2\langle \kappa \rangle +d+a\ge 3$
is not valid for
 $d\ge 1$
and
$d\ge 1$
and
 $a\in (1,2)\cup (2,\infty )$
.
$a\in (1,2)\cup (2,\infty )$
.
5 Image of the Schwartz space
In this section, for the
![]() $(\kappa ,a)$
-generalized Fourier transform, we study the image of the Schwartz space
$(\kappa ,a)$
-generalized Fourier transform, we study the image of the Schwartz space
![]() $\mathcal {S}(\mathbb {R}^d)$
. Denote by
$\mathcal {S}(\mathbb {R}^d)$
. Denote by
![]() $\mathcal {S}(\mathbb {R}_+)$
the subspace of even functions from
$\mathcal {S}(\mathbb {R}_+)$
the subspace of even functions from
![]() $\mathcal {S}(\mathbb {R})$
.
$\mathcal {S}(\mathbb {R})$
.
5.1 The case of
 $a>0$
$a>0$
Let
![]() $d\nu _{\eta }(u)=b_{\eta }u^{2\eta +1}\,du$
,
$d\nu _{\eta }(u)=b_{\eta }u^{2\eta +1}\,du$
,
![]() $b_{\eta }^{-1}=2^{\eta }\Gamma (\eta +1)$
,
$b_{\eta }^{-1}=2^{\eta }\Gamma (\eta +1)$
,
![]() $d\nu _{\eta ,a}(u)=b_{\eta ,a}u^{2\eta +a-1}du$
,
$d\nu _{\eta ,a}(u)=b_{\eta ,a}u^{2\eta +a-1}du$
,
![]() $b_{\eta ,a}^{-1}=a^{2\eta /a}\Gamma (2\eta /a+1)$
,
$b_{\eta ,a}^{-1}=a^{2\eta /a}\Gamma (2\eta /a+1)$
,
be the Hankel transform and
the a-deformed Hankel transform (see [Reference Ben Saïd, Kobayashi and Ørsted4, Reference Gorbachev, Ivanov and Tikhonov15]).
Recall that
![]() $\lambda _{\kappa }=\langle \kappa \rangle +(d-2)/2$
,
$\lambda _{\kappa }=\langle \kappa \rangle +(d-2)/2$
,
![]() $\lambda =\lambda _{\kappa ,a}=2\lambda _{\kappa }/a$
.
$\lambda =\lambda _{\kappa ,a}=2\lambda _{\kappa }/a$
.
Example 5.1. Consider
![]() $f(x)=e^{-|x|^2}\in \mathcal {S}(\mathbb {R}^d)$
,
$f(x)=e^{-|x|^2}\in \mathcal {S}(\mathbb {R}^d)$
,
![]() $f(x)=f_0(\rho )$
,
$f(x)=f_0(\rho )$
,
![]() $\rho =|x|$
. If
$\rho =|x|$
. If
![]() $|y|=v$
,
$|y|=v$
,
![]() $\rho =(a/2)^{1/a}u^{2/a}$
, then (see [Reference Ben Saïd, Kobayashi and Ørsted4, Reference Gorbachev, Ivanov and Tikhonov15])
$\rho =(a/2)^{1/a}u^{2/a}$
, then (see [Reference Ben Saïd, Kobayashi and Ørsted4, Reference Gorbachev, Ivanov and Tikhonov15])
 $$ \begin{align*} \mathcal{F}_{\kappa,a}(f)(y)=H_{\lambda_{\kappa},a}(f_0)(v)&= \int_{0}^{\infty}f_0(\rho)j_{\frac{2\lambda_{\kappa}}{a}}\Bigl(\frac{2}{a}\,(v\rho)^{a/2} \Bigr)\,d\nu_{\lambda_{\kappa},a}(\rho)\\ &= \int_{0}^{\infty}g_a(u)j_{\lambda}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}\,v^{a/2}u\Bigr)\,d\nu_{\lambda}(u), \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\kappa,a}(f)(y)=H_{\lambda_{\kappa},a}(f_0)(v)&= \int_{0}^{\infty}f_0(\rho)j_{\frac{2\lambda_{\kappa}}{a}}\Bigl(\frac{2}{a}\,(v\rho)^{a/2} \Bigr)\,d\nu_{\lambda_{\kappa},a}(\rho)\\ &= \int_{0}^{\infty}g_a(u)j_{\lambda}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}\,v^{a/2}u\Bigr)\,d\nu_{\lambda}(u), \end{align*} $$
where
Assuming that
![]() $\mathcal {F}_{\kappa ,a}(f)(y)$
is rapidly decreasing at infinity, the same is true for the function
$\mathcal {F}_{\kappa ,a}(f)(y)$
is rapidly decreasing at infinity, the same is true for the function
Considering even extensions of the functions
![]() $g_a$
and
$g_a$
and
![]() $G_a$
, we get the following representation via the Dunkl transform:
$G_a$
, we get the following representation via the Dunkl transform:
If
![]() $2/a$
is a noninteger, then either
$2/a$
is a noninteger, then either
![]() $4/a\not \in \mathbb {N}$
or
$4/a\not \in \mathbb {N}$
or
![]() $4/a=2s+1$
,
$4/a=2s+1$
,
![]() $s\in \mathbb {Z}_+$
, and the function
$s\in \mathbb {Z}_+$
, and the function
has finite smoothness at the origin. On the other hand, since
![]() $g_a,G_a\in L^1(\mathbb {R},d\mu _{\kappa ,2})$
, we obtain
$g_a,G_a\in L^1(\mathbb {R},d\mu _{\kappa ,2})$
, we obtain
and the right-hand side is infinitely differentiable at the origin if
![]() $G_a(v)$
is fast decreasing. This contradiction shows that, for
$G_a(v)$
is fast decreasing. This contradiction shows that, for
![]() $2/a\not \in \mathbb {N}$
,
$2/a\not \in \mathbb {N}$
,
![]() $\mathcal {F}_{\kappa ,a}(f)(y)$
cannot rapidly decay at infinity and so it is not a Schwartz function.
$\mathcal {F}_{\kappa ,a}(f)(y)$
cannot rapidly decay at infinity and so it is not a Schwartz function.
Moreover, let us denote for convenience the derivative of f by
![]() $\partial f$
. Since
$\partial f$
. Since
 $$\begin{align*}(\partial_v^2j_{\lambda}(uv))\bigr|_{v=0}=-\frac{u^2}{2(\lambda+1)},\quad (\partial_v^4j_{\lambda}(uv))\bigr|_{v=0}=\frac{3u^4}{4(\lambda+1)(\lambda+2)}, \end{align*}$$
$$\begin{align*}(\partial_v^2j_{\lambda}(uv))\bigr|_{v=0}=-\frac{u^2}{2(\lambda+1)},\quad (\partial_v^4j_{\lambda}(uv))\bigr|_{v=0}=\frac{3u^4}{4(\lambda+1)(\lambda+2)}, \end{align*}$$
then
and
If a is not even, then
![]() $\mathcal {F}_{\kappa ,a}(f)(y)$
has finite smoothness at the origin.
$\mathcal {F}_{\kappa ,a}(f)(y)$
has finite smoothness at the origin.
The following statement follows from Example 5.1.
Proposition 5.2. Let
![]() $d\in \mathbb {N}$
.
$d\in \mathbb {N}$
.
-
(i) The condition
 $\frac {a}{2}\in \mathbb {N}$
is necessary for the embedding
$\frac {a}{2}\in \mathbb {N}$
is necessary for the embedding
 $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))\subset C^{\infty }(\mathbb {R}^d)$
to hold.
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))\subset C^{\infty }(\mathbb {R}^d)$
to hold. -
(ii) The condition
 $\frac {2}{a}\in \mathbb {N}$
is necessary for the set
$\frac {2}{a}\in \mathbb {N}$
is necessary for the set
 $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))$
to consist of rapidly decreasing functions at infinity.
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))$
to consist of rapidly decreasing functions at infinity.
Remark 5.3. We see that
![]() $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))=\mathcal {S}(\mathbb {R}^d)$
only for
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}^d))=\mathcal {S}(\mathbb {R}^d)$
only for
![]() $a=2$
. Hence, the claim in [Reference Johansen18, Lemma 2.12] that the Schwartz space is invariant under the generalized Fourier transform is false for
$a=2$
. Hence, the claim in [Reference Johansen18, Lemma 2.12] that the Schwartz space is invariant under the generalized Fourier transform is false for
![]() $a\neq 2$
.
$a\neq 2$
.
The conditions in Proposition 5.2 are also sufficient, at least in the one-dimensional case. Indeed, suppose
![]() $\lambda =(2\kappa -1)/a\ge -1/2$
and denote the even and odd parts of f, as usual, by
$\lambda =(2\kappa -1)/a\ge -1/2$
and denote the even and odd parts of f, as usual, by
Then the one-dimensional generalized Fourier transform can be written as
Putting in (5.1)
 $$ \begin{align} \begin{gathered} x=x(u)=\Bigl(\frac{a}{2}\Bigr)^{\frac{1}{a}}\,u^{\frac{2}{a}},\quad g(u)=Af(u)=f(x(u))=f\Bigl(\Bigl(\frac{a}{2}\Bigr)^{\frac{1}{a}}\,u^{\frac{2}{a}}\Bigr),\\ g_e(u)=Af_e(u),\quad g_o(u)=Af_o(u),\quad x,u\in\mathbb{R}_+, \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} x=x(u)=\Bigl(\frac{a}{2}\Bigr)^{\frac{1}{a}}\,u^{\frac{2}{a}},\quad g(u)=Af(u)=f(x(u))=f\Bigl(\Bigl(\frac{a}{2}\Bigr)^{\frac{1}{a}}\,u^{\frac{2}{a}}\Bigr),\\ g_e(u)=Af_e(u),\quad g_o(u)=Af_o(u),\quad x,u\in\mathbb{R}_+, \end{gathered} \end{align} $$
and taking into account (2.1), we deduce
 $$ \begin{align} \mathcal{F}_{\kappa,a}(f)(y)&=\int_{0}^{\infty}Af_e(u)j_{\lambda} \Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}u\Bigr)\,d\nu_{\lambda}(u)\notag \\ &\quad \ {}+e^{-\frac{\pi i}{a}}\Bigl(\frac{2}{a}\Bigr)^{1/a}y\int_{0}^{\infty}u^{-2/a}Af_o(u) j_{\lambda+\frac{2}{a}}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2} |y|^{a/2}u\Bigr)\,d\nu_{\lambda+\frac{2}{a}}(u)\notag \\ &\qquad\qquad =H_{\lambda}(g_e)\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}\Bigr)+ e^{-\frac{\pi i}{a}} \Bigl(\frac{2}{a}\Bigr)^{1/a} yH_{\lambda+\frac{2}{a}}(u^{-2/a}g_o)\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}\Bigr). \end{align} $$
$$ \begin{align} \mathcal{F}_{\kappa,a}(f)(y)&=\int_{0}^{\infty}Af_e(u)j_{\lambda} \Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}u\Bigr)\,d\nu_{\lambda}(u)\notag \\ &\quad \ {}+e^{-\frac{\pi i}{a}}\Bigl(\frac{2}{a}\Bigr)^{1/a}y\int_{0}^{\infty}u^{-2/a}Af_o(u) j_{\lambda+\frac{2}{a}}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2} |y|^{a/2}u\Bigr)\,d\nu_{\lambda+\frac{2}{a}}(u)\notag \\ &\qquad\qquad =H_{\lambda}(g_e)\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}\Bigr)+ e^{-\frac{\pi i}{a}} \Bigl(\frac{2}{a}\Bigr)^{1/a} yH_{\lambda+\frac{2}{a}}(u^{-2/a}g_o)\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}|y|^{a/2}\Bigr). \end{align} $$
If
![]() $f\in \mathcal {S}(\mathbb {R})$
, then
$f\in \mathcal {S}(\mathbb {R})$
, then
![]() $g_e(u)$
,
$g_e(u)$
,
![]() $u^{-2/a}g_o(u)$
decrease rapidly at infinity and there exist
$u^{-2/a}g_o(u)$
decrease rapidly at infinity and there exist
Therefore, the representation (5.3) shows that, for even a, we have the embedding
![]() $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
.
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
.
Further, if
![]() $\frac {2}{a}\in \mathbb {N}$
,
$\frac {2}{a}\in \mathbb {N}$
,
![]() $f\in \mathcal {S}(\mathbb {R})$
, then the functions
$f\in \mathcal {S}(\mathbb {R})$
, then the functions
![]() $g_e(u),u^{-2/a}g_o(u) \in \mathcal {S}(\mathbb {R}_+)$
as well as (see [Reference Rösler20]) the even functions
$g_e(u),u^{-2/a}g_o(u) \in \mathcal {S}(\mathbb {R}_+)$
as well as (see [Reference Rösler20]) the even functions
Hence, we prove the following
Proposition 5.4. Suppose
![]() $\frac {2}{a}\in \mathbb {N}$
,
$\frac {2}{a}\in \mathbb {N}$
,
![]() $\lambda \ge -1/2$
,
$\lambda \ge -1/2$
,
![]() $f\in \mathcal {S}(\mathbb {R})$
, then
$f\in \mathcal {S}(\mathbb {R})$
, then
where the even functions
![]() $F_1,F_2\in \mathcal {S}(\mathbb {R})$
.
$F_1,F_2\in \mathcal {S}(\mathbb {R})$
.
Thus, for
![]() $2/a\in \mathbb {N}$
, the generalized Fourier transform decreases rapidly at infinity and we arrive at the following result.
$2/a\in \mathbb {N}$
, the generalized Fourier transform decreases rapidly at infinity and we arrive at the following result.
Proposition 5.5.
-
(i) The embedding
 $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
is valid if and only if
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
is valid if and only if
 $\frac {a}{2}\in \mathbb {N}$
.
$\frac {a}{2}\in \mathbb {N}$
. -
(ii) The set
 $\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))$
consists of rapidly decreasing functions at infinity if and only if
$\mathcal {F}_{\kappa ,a}(\mathcal {S}(\mathbb {R}))$
consists of rapidly decreasing functions at infinity if and only if
 $\frac {2}{a}\in \mathbb {N}$
.
$\frac {2}{a}\in \mathbb {N}$
.
Let
The class
![]() $\mathcal {S}_{org}(\mathbb {R})$
is dense in
$\mathcal {S}_{org}(\mathbb {R})$
is dense in
![]() $L^{2}(\mathbb {R},d\mu _{\kappa ,a})$
. Suppose
$L^{2}(\mathbb {R},d\mu _{\kappa ,a})$
. Suppose
![]() $a>0$
,
$a>0$
,
![]() $f(x)\in \mathcal {S}_{org}(\mathbb {R})$
, then the functions
$f(x)\in \mathcal {S}_{org}(\mathbb {R})$
, then the functions
![]() $g_e(u),u^{-2/a}g_o(u)$
belong to
$g_e(u),u^{-2/a}g_o(u)$
belong to
![]() $\mathcal {S}(\mathbb {R}_+)$
, cf. (5.3). Therefore, the even functions
$\mathcal {S}(\mathbb {R}_+)$
, cf. (5.3). Therefore, the even functions
![]() $H_{\lambda }(g_e)(v)$
,
$H_{\lambda }(g_e)(v)$
,
![]() $H_{\lambda +\frac {2}{a}}(u^{-2/a}g_o)(v)$
also belong to
$H_{\lambda +\frac {2}{a}}(u^{-2/a}g_o)(v)$
also belong to
![]() $\mathcal {S}(\mathbb {R})$
.
$\mathcal {S}(\mathbb {R})$
.
Thus, we obtain the following
Proposition 5.6. Suppose
![]() $a>0$
,
$a>0$
,
![]() $\lambda \ge -1/2$
, and
$\lambda \ge -1/2$
, and
![]() $f\in \mathcal {S}_{org}(\mathbb {R})$
; then the generalized Fourier transform
$f\in \mathcal {S}_{org}(\mathbb {R})$
; then the generalized Fourier transform
![]() $\mathcal {F}_{\kappa ,a}(f)$
enjoys the representation (5.4).
$\mathcal {F}_{\kappa ,a}(f)$
enjoys the representation (5.4).
5.2 The case of irrational a
We will show that if a is irrational, any nontrivial Schwartz function possesses similar properties to the Gaussian function in Example 5.1. To see this, we need auxiliary properties of the kernel of the generalized Fourier transform.
Let
![]() $\mathbb {S}^{d-1}$
be the unit sphere in
$\mathbb {S}^{d-1}$
be the unit sphere in
![]() $\mathbb {R}^{d}$
,
$\mathbb {R}^{d}$
,
![]() $x=\rho x'$
,
$x=\rho x'$
,
![]() $\rho =|x|\in \mathbb {R}_+$
,
$\rho =|x|\in \mathbb {R}_+$
,
![]() $x'\in \mathbb {S}^{d-1}$
, and
$x'\in \mathbb {S}^{d-1}$
, and
![]() $dx'$
be the Lebesgue measure on the sphere. If
$dx'$
be the Lebesgue measure on the sphere. If
![]() $a_{\kappa }^{-1}=\int _{\mathbb {S}^{d-1}}v_{\kappa }(x')\,dx'$
,
$a_{\kappa }^{-1}=\int _{\mathbb {S}^{d-1}}v_{\kappa }(x')\,dx'$
,
![]() $d\sigma _{\kappa }(x')=a_{\kappa }v_{\kappa }(x')\,dx'$
, then
$d\sigma _{\kappa }(x')=a_{\kappa }v_{\kappa }(x')\,dx'$
, then
![]() $d\mu _{\kappa ,a}(x)=d\nu _{\lambda _{\kappa },a}(\rho )\,d\sigma _{\kappa }(x')$
and
$d\mu _{\kappa ,a}(x)=d\nu _{\lambda _{\kappa },a}(\rho )\,d\sigma _{\kappa }(x')$
and
![]() $c_{\kappa ,a}=b_{\kappa ,a}a_{\kappa }$
.
$c_{\kappa ,a}=b_{\kappa ,a}a_{\kappa }$
.
Denote by
![]() $\mathcal {H}_{n}^{d}(v_{\kappa })$
the subspace of
$\mathcal {H}_{n}^{d}(v_{\kappa })$
the subspace of
![]() $\kappa $
-spherical harmonics of degree
$\kappa $
-spherical harmonics of degree
![]() $n\in \mathbb {Z}_{+}$
in
$n\in \mathbb {Z}_{+}$
in
![]() $L^{2} (\mathbb {S}^{d-1},d\sigma _{\kappa })$
(see [Reference Dunkl and Xu13, Chapter 5]). Let
$L^{2} (\mathbb {S}^{d-1},d\sigma _{\kappa })$
(see [Reference Dunkl and Xu13, Chapter 5]). Let
![]() $\mathcal {P}_{n}^{d}$
be the space of homogeneous polynomials of degree n in
$\mathcal {P}_{n}^{d}$
be the space of homogeneous polynomials of degree n in
![]() $\mathbb {R}^{d}$
. Then
$\mathbb {R}^{d}$
. Then
![]() $\mathcal {H}_{n}^{d}(v_{\kappa })$
is the restriction of
$\mathcal {H}_{n}^{d}(v_{\kappa })$
is the restriction of
![]() $\ker \Delta _{\kappa }\cap \mathcal {P}_{n}^{d}$
to the sphere
$\ker \Delta _{\kappa }\cap \mathcal {P}_{n}^{d}$
to the sphere
![]() $\mathbb {S}^{d-1}$
.
$\mathbb {S}^{d-1}$
.
If
![]() $l_{n}$
is the dimension of
$l_{n}$
is the dimension of
![]() $\mathcal {H}_{n}^{d}(v_{\kappa })$
, we denote by
$\mathcal {H}_{n}^{d}(v_{\kappa })$
, we denote by
![]() $\{Y_{n}^{j}\colon j=1,\ldots ,l_{n}\}$
the real-valued orthonormal basis of
$\{Y_{n}^{j}\colon j=1,\ldots ,l_{n}\}$
the real-valued orthonormal basis of
![]() $\mathcal {H}_{n}^{d}(v_{\kappa })$
in
$\mathcal {H}_{n}^{d}(v_{\kappa })$
in
![]() $L^{2}(\mathbb {S}^{d-1},d\sigma _{\kappa })$
. A union of these bases forms an orthonormal basis in
$L^{2}(\mathbb {S}^{d-1},d\sigma _{\kappa })$
. A union of these bases forms an orthonormal basis in
![]() $L^{2}(\mathbb {S}^{d-1},d\sigma _{\kappa })$
consisting of k-spherical harmonics.
$L^{2}(\mathbb {S}^{d-1},d\sigma _{\kappa })$
consisting of k-spherical harmonics.
Let us rewrite (4.3) as follows
 $$\begin{align*}B_{\kappa,a}(x,y) =\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\lambda_{\kappa}+j}{\lambda_{\kappa}}\,\frac{\Gamma(2\lambda_{\kappa}/a+1)(|x||y|)^{j}}{a^{2j/a}\,\Gamma(2(\lambda_{\kappa}+j)/a+1)}\, j_{\frac{2(\lambda_{\kappa}+j)}{a}}\Bigl(\frac{2}{a}\,(|x||y|)^{a/2}\Bigr)V_{\kappa}C_{j}^{\lambda_{\kappa}}(\langle x',{\cdot}\,\rangle)(y'). \end{align*}$$
$$\begin{align*}B_{\kappa,a}(x,y) =\sum_{j=0}^{\infty}e^{-\frac{i\pi j}{a}}\,\frac{\lambda_{\kappa}+j}{\lambda_{\kappa}}\,\frac{\Gamma(2\lambda_{\kappa}/a+1)(|x||y|)^{j}}{a^{2j/a}\,\Gamma(2(\lambda_{\kappa}+j)/a+1)}\, j_{\frac{2(\lambda_{\kappa}+j)}{a}}\Bigl(\frac{2}{a}\,(|x||y|)^{a/2}\Bigr)V_{\kappa}C_{j}^{\lambda_{\kappa}}(\langle x',{\cdot}\,\rangle)(y'). \end{align*}$$
Integrating this and using orthogonality of
![]() $\kappa $
-spherical harmonics, as in the case of the Dunkl kernel (see [Reference Dunkl and Xu13, Theorem 5.3.4], [Reference Rösler21, Corollary 2.5]), we obtain the following crucial property of the kernel of the generalized Fourier transform.
$\kappa $
-spherical harmonics, as in the case of the Dunkl kernel (see [Reference Dunkl and Xu13, Theorem 5.3.4], [Reference Rösler21, Corollary 2.5]), we obtain the following crucial property of the kernel of the generalized Fourier transform.
Proposition 5.7. If
![]() $x,y\in \mathbb {R}^d$
,
$x,y\in \mathbb {R}^d$
,
![]() $x=\rho x'$
,
$x=\rho x'$
,
![]() $y=vy'$
, then
$y=vy'$
, then
 $$\begin{align*}\int_{\mathbb{S}^{d-1}}B_{\kappa,a}(x,vy')Y_{n}^{j}(y')\,d\sigma_{\kappa}(y')=\frac{e^{-\frac{i\pi n}{a}}\Gamma(2\lambda_{\kappa}/a+1)}{a^{2n/a} \,\Gamma(2(\lambda_{\kappa}+n)/a+1)}\,v^n j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)Y_n^j(x). \end{align*}$$
$$\begin{align*}\int_{\mathbb{S}^{d-1}}B_{\kappa,a}(x,vy')Y_{n}^{j}(y')\,d\sigma_{\kappa}(y')=\frac{e^{-\frac{i\pi n}{a}}\Gamma(2\lambda_{\kappa}/a+1)}{a^{2n/a} \,\Gamma(2(\lambda_{\kappa}+n)/a+1)}\,v^n j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)Y_n^j(x). \end{align*}$$
Proposition 5.8. For irrational a and a nontrivial function
![]() $f\in \mathcal {S}(\mathbb {R}^d)$
, we have
$f\in \mathcal {S}(\mathbb {R}^d)$
, we have
![]() $\mathcal {F}_{\kappa ,a}(f)\notin \mathcal {S}(\mathbb {R}^d)$
.
$\mathcal {F}_{\kappa ,a}(f)\notin \mathcal {S}(\mathbb {R}^d)$
.
Proof.
1. First, assume that
![]() $f(x)=\rho ^n\psi (\rho )Y_n^j(x')$
, where
$f(x)=\rho ^n\psi (\rho )Y_n^j(x')$
, where
![]() $n\in \mathbb {Z}_+$
,
$n\in \mathbb {Z}_+$
,
![]() $x=\rho x'$
,
$x=\rho x'$
,
![]() $|x'|=1$
, and
$|x'|=1$
, and
![]() $\psi \in \mathcal {S}(\mathbb {R}_+)$
. Since
$\psi \in \mathcal {S}(\mathbb {R}_+)$
. Since
![]() $\rho ^nY_n^j(x')=Y_n^j(x)$
is a homogeneous polynomial of degree n, then
$\rho ^nY_n^j(x')=Y_n^j(x)$
is a homogeneous polynomial of degree n, then
![]() $f(x)=\psi (|x|)Y_n^j(x)\in \mathcal {S}(\mathbb {R}^d)$
. If
$f(x)=\psi (|x|)Y_n^j(x)\in \mathcal {S}(\mathbb {R}^d)$
. If
![]() $y=vy'$
,
$y=vy'$
,
![]() $\rho =(a/2)^{1/a}u^{2/a}$
, then by [Reference Gorbachev, Ivanov and Tikhonov15]
$\rho =(a/2)^{1/a}u^{2/a}$
, then by [Reference Gorbachev, Ivanov and Tikhonov15]
 $$ \begin{align*} \mathcal{F}_{\kappa,a}(f)(y)=e^{-\frac{i\pi n}{a}}Y_n^j(y)&H_{\lambda_{\kappa}+n,a}(\psi)(v) =e^{-\frac{i\pi n}{a}}Y_n^j(y)\int_{0}^{\infty}\psi(\rho) j_{\frac{2(\lambda_{\kappa}+n)}{a}} \Bigl(\frac{2}{a}\,(v\rho)^{a/2} \Bigr)\,d\nu_{\lambda_{\kappa},a}(\rho)\\ & =e^{-\frac{i\pi n}{a}}Y_n^j(y)\int_{0}^{\infty}\psi\Bigl(\Bigl(\frac{a}{2}\Bigr)^{1/a}u^{2/a}\Bigr) j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}\,v^{a/2}u \Bigr)\,d\nu_{\frac{2(\lambda_{\kappa}+n)}{a}}(u). \end{align*} $$
$$ \begin{align*} \mathcal{F}_{\kappa,a}(f)(y)=e^{-\frac{i\pi n}{a}}Y_n^j(y)&H_{\lambda_{\kappa}+n,a}(\psi)(v) =e^{-\frac{i\pi n}{a}}Y_n^j(y)\int_{0}^{\infty}\psi(\rho) j_{\frac{2(\lambda_{\kappa}+n)}{a}} \Bigl(\frac{2}{a}\,(v\rho)^{a/2} \Bigr)\,d\nu_{\lambda_{\kappa},a}(\rho)\\ & =e^{-\frac{i\pi n}{a}}Y_n^j(y)\int_{0}^{\infty}\psi\Bigl(\Bigl(\frac{a}{2}\Bigr)^{1/a}u^{2/a}\Bigr) j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\Bigl(\frac{2}{a}\Bigr)^{1/2}\,v^{a/2}u \Bigr)\,d\nu_{\frac{2(\lambda_{\kappa}+n)}{a}}(u). \end{align*} $$
Moreover, following the ideas used in Example 5.1, we obtain that the function
with irrational a cannot decrease rapidly as
![]() $v\to \infty $
, and it has finite smoothness at the origin. Therefore, it follows that
$v\to \infty $
, and it has finite smoothness at the origin. Therefore, it follows that
![]() $\mathcal {F}_{\kappa ,a}(f)\notin \mathcal {S}(\mathbb {R}^d)$
.
$\mathcal {F}_{\kappa ,a}(f)\notin \mathcal {S}(\mathbb {R}^d)$
.
2. Let now
![]() $f\in \mathcal {S}(\mathbb {R}^d)$
be any nonzero function. Then its spherical
$f\in \mathcal {S}(\mathbb {R}^d)$
be any nonzero function. Then its spherical
![]() $\kappa $
-harmonic expansion is given by
$\kappa $
-harmonic expansion is given by
 $$\begin{align*}f(\rho x')=\sum_{n=0}^{\infty}\sum_{j=1}^{l_{n}}f_{nj}(\rho)Y_{n}^{j}(x'),\quad f_{nj}(\rho)=\int_{\mathbb{S}^{d-1}}f(\rho x')Y_{n}^{j}(x')\,d\sigma_{\kappa}(x') \end{align*}$$
$$\begin{align*}f(\rho x')=\sum_{n=0}^{\infty}\sum_{j=1}^{l_{n}}f_{nj}(\rho)Y_{n}^{j}(x'),\quad f_{nj}(\rho)=\int_{\mathbb{S}^{d-1}}f(\rho x')Y_{n}^{j}(x')\,d\sigma_{\kappa}(x') \end{align*}$$
(see [Reference Gorbachev, Ivanov and Tikhonov15]). Since the subspaces
![]() $\mathcal {H}_n^d(v_{\kappa })$
are orthogonal, then
$\mathcal {H}_n^d(v_{\kappa })$
are orthogonal, then
![]() $f_{nj}^{(j)}(0)=0$
,
$f_{nj}^{(j)}(0)=0$
,
![]() $j=0,1,\dots ,n-1$
. Changing variables
$j=0,1,\dots ,n-1$
. Changing variables
![]() $x'\to -x'$
implies
$x'\to -x'$
implies
![]() $f_{nj}(-\rho ) =(-1)^nf_{nj}(\rho ). $
Hence, setting a nonzero function
$f_{nj}(-\rho ) =(-1)^nf_{nj}(\rho ). $
Hence, setting a nonzero function
![]() $g_{nj}(f)(x)=f_{nj}(\rho )Y_{n}^{j}(x')\in \mathcal {S}(\mathbb {R}^d)$
, we have
$g_{nj}(f)(x)=f_{nj}(\rho )Y_{n}^{j}(x')\in \mathcal {S}(\mathbb {R}^d)$
, we have
![]() $g_{nj}(x)=\rho ^n\psi (\rho )Y_{n}^{j}(x')$
with some
$g_{nj}(x)=\rho ^n\psi (\rho )Y_{n}^{j}(x')$
with some
![]() $\psi \in \mathcal {S}(\mathbb {R}_+)$
.
$\psi \in \mathcal {S}(\mathbb {R}_+)$
.
In order to apply the results obtained in case 1, we need to show that
Indeed, we note that
On the other hand, in view of Proposition 5.7, we deduce that
 $$ \begin{align*} g_{nj}(\mathcal{F}_{\kappa,a}(f))(y)&=Y_{n}^{j}(y')\int_{\mathbb{S}^{d-1}}\mathcal{F}_{\kappa,a}(f)(vy')Y_{n}^{j}(y')\,d\sigma_{\kappa,a}(y')\\ &=e^{-\frac{i\pi n}{a}}Y_{n}^{j}(y) \int_{\mathbb{R}^d}\frac{f(x)\Gamma(2\lambda_{\kappa}/a+1)}{a^{2n/a} \,\Gamma(2(\lambda_{\kappa}+n)/a+1)} j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)Y_n^j(x)\,d\mu_{\kappa,a}(x) \\ &=e^{-\frac{i\pi n}{a}}Y_{n}^{j}(y)\int_{0}^{\infty}\psi(\rho) j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)\,d\nu_{\lambda_{\kappa}+n,a}(\rho)\\ &=e^{-\frac{i\pi n}{a}}Y_n^j(y)H_{\lambda_{\kappa}+n,a}(\psi)(v). \end{align*} $$
$$ \begin{align*} g_{nj}(\mathcal{F}_{\kappa,a}(f))(y)&=Y_{n}^{j}(y')\int_{\mathbb{S}^{d-1}}\mathcal{F}_{\kappa,a}(f)(vy')Y_{n}^{j}(y')\,d\sigma_{\kappa,a}(y')\\ &=e^{-\frac{i\pi n}{a}}Y_{n}^{j}(y) \int_{\mathbb{R}^d}\frac{f(x)\Gamma(2\lambda_{\kappa}/a+1)}{a^{2n/a} \,\Gamma(2(\lambda_{\kappa}+n)/a+1)} j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)Y_n^j(x)\,d\mu_{\kappa,a}(x) \\ &=e^{-\frac{i\pi n}{a}}Y_{n}^{j}(y)\int_{0}^{\infty}\psi(\rho) j_{\frac{2(\lambda_{\kappa}+n)}{a}}\Bigl(\frac{2}{a}\,(\rho v)^{a/2}\Bigr)\,d\nu_{\lambda_{\kappa}+n,a}(\rho)\\ &=e^{-\frac{i\pi n}{a}}Y_n^j(y)H_{\lambda_{\kappa}+n,a}(\psi)(v). \end{align*} $$
Assuming here that
![]() $f,\mathcal {F}_{\kappa ,a}(f)\in \mathcal {S}(\mathbb {R}^d)$
yields
$f,\mathcal {F}_{\kappa ,a}(f)\in \mathcal {S}(\mathbb {R}^d)$
yields
![]() $g_{nj}(f),\mathcal {F}_{\kappa ,a}(g_{nj}(f))\in \mathcal {S}(\mathbb {R}^d)$
, which contradicts the first case.
$g_{nj}(f),\mathcal {F}_{\kappa ,a}(g_{nj}(f))\in \mathcal {S}(\mathbb {R}^d)$
, which contradicts the first case.
Summarizing, the generalized Fourier transform for irrational a drastically deforms even very smooth functions. It was mentioned in [Reference Ben Saïd, Kobayashi and Ørsted4, Chapter 5] that the generalized Fourier transform has a finite order only for rational a. Therefore, the case of irrational a is of little interest in harmonic analysis.
6 Nondeformed unitary transforms generated by
 $\mathcal {F}_{\kappa ,a}$
$\mathcal {F}_{\kappa ,a}$
Let
![]() $a=\frac {2}{2r+1}$
and
$a=\frac {2}{2r+1}$
and
![]() $\lambda =\lambda _{\kappa ,a}=(2\kappa -1)/a\ge -1/2$
. Recalling that A is given by (5.2), we may assume that
$\lambda =\lambda _{\kappa ,a}=(2\kappa -1)/a\ge -1/2$
. Recalling that A is given by (5.2), we may assume that
![]() $x, u\in \mathbb {R}$
. Since
$x, u\in \mathbb {R}$
. Since
 $$\begin{align*}\int_{-\infty}^{\infty}|f(x)|^2\,d\mu_{\kappa,a}(x)=\int_{-\infty}^{\infty}|Af(u)|^2\,d\widetilde{\nu}_{\lambda}(u),\qquad d\widetilde{\nu}_{\lambda}(u) =\frac{|u|^{2\lambda+1}\,du}{2^{\lambda+1} \Gamma(\lambda+1)}, \end{align*}$$
$$\begin{align*}\int_{-\infty}^{\infty}|f(x)|^2\,d\mu_{\kappa,a}(x)=\int_{-\infty}^{\infty}|Af(u)|^2\,d\widetilde{\nu}_{\lambda}(u),\qquad d\widetilde{\nu}_{\lambda}(u) =\frac{|u|^{2\lambda+1}\,du}{2^{\lambda+1} \Gamma(\lambda+1)}, \end{align*}$$
the linear operator
![]() $A\colon L^{2}(\mathbb {R},d\mu _{\kappa ,a})\to L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
is an isometric isomorphism and the inverse operator is given by
$A\colon L^{2}(\mathbb {R},d\mu _{\kappa ,a})\to L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
is an isometric isomorphism and the inverse operator is given by
![]() $A^{-1}g(x)=g((2r+1)^{1/2}\,x^{1/(2r+1)})$
.
$A^{-1}g(x)=g((2r+1)^{1/2}\,x^{1/(2r+1)})$
.
In view of (2.4) and (5.2),
![]() $B_{\kappa ,a}(x,y)=e_{2r+1}(uv,\lambda )$
and
$B_{\kappa ,a}(x,y)=e_{2r+1}(uv,\lambda )$
and
This formula defines the nondeformed transform
![]() $\mathcal {F}_{r}^{\lambda }$
, for
$\mathcal {F}_{r}^{\lambda }$
, for
![]() $\lambda> -1/2$
and
$\lambda> -1/2$
and
![]() $r\in \mathbb {Z}_+$
,
$r\in \mathbb {Z}_+$
,
 $$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)&=\int_{-\infty}^{\infty}e_{2r+1}(uv,\lambda)g(u) \,d\widetilde{\nu}_{\lambda}(u)\\ &=\int_{-\infty}^{\infty}\Bigl(j_{\lambda}(uv)+i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(uv)\Bigr)g(u) \,d\widetilde{\nu}_{\lambda}(u)\\ &=c_{\lambda}\int_{-\infty}^{\infty}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))\,e^{-iuvt}\,dt\,g(u) \,d\widetilde{\nu}_{\lambda}(u). \end{align*} $$
$$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)&=\int_{-\infty}^{\infty}e_{2r+1}(uv,\lambda)g(u) \,d\widetilde{\nu}_{\lambda}(u)\\ &=\int_{-\infty}^{\infty}\Bigl(j_{\lambda}(uv)+i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\, j_{\lambda+2r+1}(uv)\Bigr)g(u) \,d\widetilde{\nu}_{\lambda}(u)\\ &=c_{\lambda}\int_{-\infty}^{\infty}\int_{-1}^{1}(1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))\,e^{-iuvt}\,dt\,g(u) \,d\widetilde{\nu}_{\lambda}(u). \end{align*} $$
Moreover, its kernel satisfies the estimate
![]() $|e_{2r+1}(uv,\lambda )|\le M_{\lambda }<\infty $
and, importantly,
$|e_{2r+1}(uv,\lambda )|\le M_{\lambda }<\infty $
and, importantly,
![]() $M_{\lambda }=1$
for
$M_{\lambda }=1$
for
![]() $\lambda \ge 0$
. If
$\lambda \ge 0$
. If
![]() $r=0$
, we recover the one-dimensional Dunkl transform. Below, we study invariant subspaces (
$r=0$
, we recover the one-dimensional Dunkl transform. Below, we study invariant subspaces (
![]() $\subset C^{\infty }$
) of the
$\subset C^{\infty }$
) of the
![]() $\mathcal {F}_{r}^{\lambda }$
transform. The Plancherel theorem for
$\mathcal {F}_{r}^{\lambda }$
transform. The Plancherel theorem for
![]() $\mathcal {F}_{\kappa ,a}$
given by
$\mathcal {F}_{\kappa ,a}$
given by
implies that
![]() $\mathcal {F}_{r}^{\lambda }$
is a unitary operator in
$\mathcal {F}_{r}^{\lambda }$
is a unitary operator in
![]() $L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
, that is
$L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
, that is
Since the reverse operator satisfies
![]() $(\mathcal {F}_{\kappa ,a})^{-1}(f)(x)=\mathcal {F}_{\kappa ,a}(f)(-x)$
[Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.3], we have
$(\mathcal {F}_{\kappa ,a})^{-1}(f)(x)=\mathcal {F}_{\kappa ,a}(f)(-x)$
[Reference Ben Saïd, Kobayashi and Ørsted4, Theorem 5.3], we have
If
![]() $g, \mathcal {F}_{r}^{\lambda }(g)\in L^{1}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
, then one may assume that
$g, \mathcal {F}_{r}^{\lambda }(g)\in L^{1}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
, then one may assume that
![]() $g, \mathcal {F}_{r}^{\lambda }(g)\in C_b(\mathbb {R})$
. Moreover, the inversion formula
$g, \mathcal {F}_{r}^{\lambda }(g)\in C_b(\mathbb {R})$
. Moreover, the inversion formula
holds not only in an
![]() $L_2$
sense but also pointwise.
$L_2$
sense but also pointwise.
Considering the derivatives of the kernel
![]() $e_{2r+1}(uv,\lambda )$
, we note that
$e_{2r+1}(uv,\lambda )$
, we note that
 $$\begin{align*}\partial_{v}^{n}e_{2r+1}(uv,\lambda)=(iu)^{n}c_{\lambda}\int_{-1}^{1}t^{n} (1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))\,e^{-iuvt}\,dt, \end{align*}$$
$$\begin{align*}\partial_{v}^{n}e_{2r+1}(uv,\lambda)=(iu)^{n}c_{\lambda}\int_{-1}^{1}t^{n} (1-t^2)^{\lambda-1/2}(1+P_{2r+1}^{(\lambda-1/2)}(t))\,e^{-iuvt}\,dt, \end{align*}$$
and so,
Then, for
![]() $g\in \mathcal {S}(\mathbb {R})$
, we have
$g\in \mathcal {S}(\mathbb {R})$
, we have
Therefore,
![]() $\mathcal {F}_{r}^{\lambda }(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
. However,
$\mathcal {F}_{r}^{\lambda }(\mathcal {S}(\mathbb {R}))\subset C^{\infty }(\mathbb {R})$
. However,
![]() $\mathcal {F}_{r}^{\lambda }(\mathcal {S}(\mathbb {R}))\not \subset \mathcal {S}(\mathbb {R})$
. Indeed, assuming
$\mathcal {F}_{r}^{\lambda }(\mathcal {S}(\mathbb {R}))\not \subset \mathcal {S}(\mathbb {R})$
. Indeed, assuming
![]() $g,\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}(\mathbb {R})$
, by orthogonality of the Gegenbauer polynomials for
$g,\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}(\mathbb {R})$
, by orthogonality of the Gegenbauer polynomials for
![]() $s=0,1,\dots ,r-1$
,
$s=0,1,\dots ,r-1$
,
 $$\begin{align*}\int_{-1}^{1}t^{2s+1} (1-t^2)^{\lambda-1/2}(1\pm P_{2r+1}^{(\lambda-1/2)}(t,\lambda))\,dt=0 \end{align*}$$
$$\begin{align*}\int_{-1}^{1}t^{2s+1} (1-t^2)^{\lambda-1/2}(1\pm P_{2r+1}^{(\lambda-1/2)}(t,\lambda))\,dt=0 \end{align*}$$
and
which is not true for arbitrary g.
Put for
![]() $n\in \mathbb {Z}_+$
$n\in \mathbb {Z}_+$
The set
![]() $\mathcal {S}_{n}(\mathbb {R})$
is dense in
$\mathcal {S}_{n}(\mathbb {R})$
is dense in
![]() $L^{2}(\mathbb {R},d\mu _{\kappa ,a})$
and in
$L^{2}(\mathbb {R},d\mu _{\kappa ,a})$
and in
![]() $L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
.
$L^{2}(\mathbb {R},d\widetilde {\nu }_{\lambda })$
.
Example 6.1. Consider the function
![]() $g_{2s+1}(u)=u^{2s+1}e^{-u^2}\in \mathcal {S}_{s}(\mathbb {R})$
,
$g_{2s+1}(u)=u^{2s+1}e^{-u^2}\in \mathcal {S}_{s}(\mathbb {R})$
,
![]() $s\in \mathbb {Z}_+$
. By means of (2.1), (2.4), [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter VI, 6.1], and [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi2, Chapter VIII, 8.6(14)], we get
$s\in \mathbb {Z}_+$
. By means of (2.1), (2.4), [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi1, Chapter VI, 6.1], and [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi2, Chapter VIII, 8.6(14)], we get
 $$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g_{2s+1})(v)&=i(-1)^{r+1}v^{-\lambda}\int_{0}^{\infty}u^{\lambda+2s+2}e^{-u^2}J_{\lambda+2r+1}(uv)\,du\\ &=ic_{r,\lambda,s}\,v^{2r+1}\sum_{l=0}^{\infty}\frac{(\lambda+s+r+2)_l}{(\lambda+2r+2)_l}\Bigl(-\frac{v^2}{4}\Bigr)^{l}\\ &=ic_{r,\lambda,s}\,v^{2r+1}\Phi\Bigl(\lambda+s+r+2,\lambda+2r+2,-\frac{v^2}{4}\Bigr),\quad c_{r,\lambda,s}>0. \end{align*} $$
$$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g_{2s+1})(v)&=i(-1)^{r+1}v^{-\lambda}\int_{0}^{\infty}u^{\lambda+2s+2}e^{-u^2}J_{\lambda+2r+1}(uv)\,du\\ &=ic_{r,\lambda,s}\,v^{2r+1}\sum_{l=0}^{\infty}\frac{(\lambda+s+r+2)_l}{(\lambda+2r+2)_l}\Bigl(-\frac{v^2}{4}\Bigr)^{l}\\ &=ic_{r,\lambda,s}\,v^{2r+1}\Phi\Bigl(\lambda+s+r+2,\lambda+2r+2,-\frac{v^2}{4}\Bigr),\quad c_{r,\lambda,s}>0. \end{align*} $$
We consider two cases. If
![]() $s=0,1,\dots ,r-1$
, then asymptotics as
$s=0,1,\dots ,r-1$
, then asymptotics as
![]() $v\to \infty $
[Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi3, Chapter VI,6.13.1] implies
$v\to \infty $
[Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi3, Chapter VI,6.13.1] implies
 $$\begin{align*}\Phi\Bigl(\lambda+s+r+2,\lambda+2r+2,-\frac{v^2}{4}\Bigr)=\frac{\Gamma(\lambda+2r+2)} {\Gamma(r-s)}\Bigl(\frac{v^2}{4}\Bigr)^{-(\lambda+s+r+2)}\Bigl(1+O\Bigl(\frac{1}{v^2}\Bigr)\Bigr), \end{align*}$$
$$\begin{align*}\Phi\Bigl(\lambda+s+r+2,\lambda+2r+2,-\frac{v^2}{4}\Bigr)=\frac{\Gamma(\lambda+2r+2)} {\Gamma(r-s)}\Bigl(\frac{v^2}{4}\Bigr)^{-(\lambda+s+r+2)}\Bigl(1+O\Bigl(\frac{1}{v^2}\Bigr)\Bigr), \end{align*}$$
that is,
![]() $\mathcal {F}_{r}^{\lambda }(g_{2s+1})\notin \mathcal {S}(\mathbb {R})$
. If
$\mathcal {F}_{r}^{\lambda }(g_{2s+1})\notin \mathcal {S}(\mathbb {R})$
. If
![]() $s\ge r$
, then applying the Kummer transform [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi3, Chapter VI,6.3.7)] gives us
$s\ge r$
, then applying the Kummer transform [Reference Bateman, Erdélyi, Magnus, Oberhettinger and Tricomi3, Chapter VI,6.3.7)] gives us
 $$ \begin{align} \mathcal{F}_{r}^{\lambda}(g_{2s+1})(v)&=ic_{r,\lambda,s}\,v^{2r+1}e^{-v^2/4} \Phi\Bigl(r-s,\lambda+2r+2,\frac{v^2}{4}\Bigr)\nonumber \\ &=ic_{r,\lambda,s}\,v^{2r+1}e^{-v^2/4} \sum_{l=0}^{s-r}\frac{(r-s)_l}{(\lambda+2r+2)_l}\Bigl(\frac{v^2}{4}\Bigr)^{l}, \end{align} $$
$$ \begin{align} \mathcal{F}_{r}^{\lambda}(g_{2s+1})(v)&=ic_{r,\lambda,s}\,v^{2r+1}e^{-v^2/4} \Phi\Bigl(r-s,\lambda+2r+2,\frac{v^2}{4}\Bigr)\nonumber \\ &=ic_{r,\lambda,s}\,v^{2r+1}e^{-v^2/4} \sum_{l=0}^{s-r}\frac{(r-s)_l}{(\lambda+2r+2)_l}\Bigl(\frac{v^2}{4}\Bigr)^{l}, \end{align} $$
that is,
![]() $\mathcal {F}_{r}^{\lambda }(g_{2s+1})(v)\in \mathcal {S}_{r}(\mathbb {R})$
.
$\mathcal {F}_{r}^{\lambda }(g_{2s+1})(v)\in \mathcal {S}_{r}(\mathbb {R})$
.
Since
![]() $g_{2r+1}\in \mathcal {S}_{r}(\mathbb {R})$
and
$g_{2r+1}\in \mathcal {S}_{r}(\mathbb {R})$
and
![]() $\mathcal {F}_{r}^{\lambda }(g_{2r+1})(v)\in \mathcal {S}_{r}(\mathbb {R})$
, one can conjecture that
$\mathcal {F}_{r}^{\lambda }(g_{2r+1})(v)\in \mathcal {S}_{r}(\mathbb {R})$
, one can conjecture that
![]() $\mathcal {F}_{r}^{\lambda }(\mathcal {S}_{r}(\mathbb {R}))= \mathcal {S}_{r}(\mathbb {R})$
. In order to show this (see Proposition 6.3), we will need some auxiliary results.
$\mathcal {F}_{r}^{\lambda }(\mathcal {S}_{r}(\mathbb {R}))= \mathcal {S}_{r}(\mathbb {R})$
. In order to show this (see Proposition 6.3), we will need some auxiliary results.
Recall that for the weight function
![]() $|x|^{2\lambda +1}$
, the differential-difference Dunkl operator of the first and second order are given by
$|x|^{2\lambda +1}$
, the differential-difference Dunkl operator of the first and second order are given by
(see [Reference Ben Saïd, Kobayashi and Ørsted4, Reference Rösler20]). Let us define the operator
which is obtained by changing variables
![]() $x=x(u)$
as in (5.2) in the Dunkl Laplacian
$x=x(u)$
as in (5.2) in the Dunkl Laplacian
By direct calculations, we verify that the kernel
![]() $e_{2r+1}(uv,\lambda )$
is the eigenfunction of
$e_{2r+1}(uv,\lambda )$
is the eigenfunction of
![]() $\delta _{\lambda }$
:
$\delta _{\lambda }$
:
Using [Reference Rösler20, Proposition 2.18] for
![]() $g\in \mathcal {S}(\mathbb {R})$
, we have
$g\in \mathcal {S}(\mathbb {R})$
, we have
Suppose
![]() $g\in \mathcal {S}_1(\mathbb {R})$
, then
$g\in \mathcal {S}_1(\mathbb {R})$
, then
and
This, (6.5) and (6.6) for any
![]() $g\in \mathcal {S}_1(\mathbb {R})$
yield
$g\in \mathcal {S}_1(\mathbb {R})$
yield
 $$ \begin{align} \int_{-\infty}^{\infty}\delta_{\lambda}g(u)e_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u)&= \int_{-\infty}^{\infty}g(u)(\delta_{\lambda})_ue_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u) \nonumber \\ &=-|v|^2\int_{-\infty}^{\infty}g(u)e_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u). \end{align} $$
$$ \begin{align} \int_{-\infty}^{\infty}\delta_{\lambda}g(u)e_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u)&= \int_{-\infty}^{\infty}g(u)(\delta_{\lambda})_ue_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u) \nonumber \\ &=-|v|^2\int_{-\infty}^{\infty}g(u)e_{2r+1}(uv,\lambda)\,d\widetilde{\nu}_{\lambda}(u). \end{align} $$
Applying (6.7) for
![]() $g\in \mathcal {S}_n(\mathbb {R})$
, we get
$g\in \mathcal {S}_n(\mathbb {R})$
, we get
Lemma 6.2. Suppose
![]() $g\in \mathcal {S}(\mathbb {R})$
, and
$g\in \mathcal {S}(\mathbb {R})$
, and
 $$\begin{align*}a_n(g)(v)=\sum_{k=0}^n\sum_{l=0}^k\frac{1}{(k-l)!}\,\frac{\partial^{2l+1}g(0)}{(2l+1)!}\,v^{2k+1}e^{-v^2}, \end{align*}$$
$$\begin{align*}a_n(g)(v)=\sum_{k=0}^n\sum_{l=0}^k\frac{1}{(k-l)!}\,\frac{\partial^{2l+1}g(0)}{(2l+1)!}\,v^{2k+1}e^{-v^2}, \end{align*}$$
then
![]() $g-a_n(g)\in \mathcal {S}_{n+1}(\mathbb {R})$
.
$g-a_n(g)\in \mathcal {S}_{n+1}(\mathbb {R})$
.
Proof. We have
![]() $g-a_n(g)\in \mathcal {S}(\mathbb {R})$
. Applying the Leibniz rule for
$g-a_n(g)\in \mathcal {S}(\mathbb {R})$
. Applying the Leibniz rule for
![]() $s=0,1,\dots ,n$
,
$s=0,1,\dots ,n$
,
 $$ \begin{align*} \frac{\partial^{2s+1}a_n(g)(0)}{(2s+1)!}&=\frac{1}{(2s+1)!}\sum_{k=0}^s\sum_{l=0}^k\frac{\partial^{2l+1}g(0)}{(k-l)!\,(2l+1)!} \binom{2s+1}{2k+1}(2k+1)!\partial^{2s-2k}(e^{-u^2})(0)\\ &=\sum_{k=0}^s\sum_{l=0}^k\frac{\partial^{2l+1}g(0)(-1)^{s+k}}{(k-l)!\,(2l+1)!\,(s-k)!} = \sum_{l=0}^s\frac{\partial^{2l+1}g(0)}{(2l+1)!}\sum_{m=0}^{s-l}\frac{(-1)^{s+l+m}}{m!\,(s-l-m)!}\\ &=\frac{1}{(s-l)!}\sum_{l=0}^s\frac{(-1)^{s+l}\partial^{2l+1}g(0)}{(s-l)!\,(2l+1)!}(1-1)^{s-l}=\frac{\partial^{2s+1}g(0)}{(2s+1)!}.\\[-40pt] \end{align*} $$
$$ \begin{align*} \frac{\partial^{2s+1}a_n(g)(0)}{(2s+1)!}&=\frac{1}{(2s+1)!}\sum_{k=0}^s\sum_{l=0}^k\frac{\partial^{2l+1}g(0)}{(k-l)!\,(2l+1)!} \binom{2s+1}{2k+1}(2k+1)!\partial^{2s-2k}(e^{-u^2})(0)\\ &=\sum_{k=0}^s\sum_{l=0}^k\frac{\partial^{2l+1}g(0)(-1)^{s+k}}{(k-l)!\,(2l+1)!\,(s-k)!} = \sum_{l=0}^s\frac{\partial^{2l+1}g(0)}{(2l+1)!}\sum_{m=0}^{s-l}\frac{(-1)^{s+l+m}}{m!\,(s-l-m)!}\\ &=\frac{1}{(s-l)!}\sum_{l=0}^s\frac{(-1)^{s+l}\partial^{2l+1}g(0)}{(s-l)!\,(2l+1)!}(1-1)^{s-l}=\frac{\partial^{2s+1}g(0)}{(2s+1)!}.\\[-40pt] \end{align*} $$
Proposition 6.3. Let
![]() $\lambda>-1/2$
and
$\lambda>-1/2$
and
![]() $r\in \mathbb {Z}_+$
. We have
$r\in \mathbb {Z}_+$
. We have
![]() $\mathcal {F}_{r}^{\lambda }(\mathcal {S}_{r}(\mathbb {R}))=\mathcal {S}_{r}(\mathbb {R})$
.
$\mathcal {F}_{r}^{\lambda }(\mathcal {S}_{r}(\mathbb {R}))=\mathcal {S}_{r}(\mathbb {R})$
.
If
![]() $r=0$
, we recover the result by de Jeu [Reference de Jeu8] for the Dunkl transform.
$r=0$
, we recover the result by de Jeu [Reference de Jeu8] for the Dunkl transform.
Proof. Let
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $g\in \mathcal {S}_{r}(\mathbb {R})$
. It is enough to show that g satisfies the condition:
$g\in \mathcal {S}_{r}(\mathbb {R})$
. It is enough to show that g satisfies the condition:
We have
Since
![]() $\partial ^{2l+1}g(0)=0$
,
$\partial ^{2l+1}g(0)=0$
,
![]() $l=0,1,\dots ,r-1$
, then
$l=0,1,\dots ,r-1$
, then
 $$\begin{align*}a_{n-1}(g)(v)=\sum_{k=r}^{n-1}\sum_{l=r}^k\frac{1}{(k-l)!}\, \frac{\partial^{2l+1}g(0)}{(2l+1)!}\,v^{2k+1}e^{-v^2}\in\mathcal{S}_{r}(\mathbb{R}). \end{align*}$$
$$\begin{align*}a_{n-1}(g)(v)=\sum_{k=r}^{n-1}\sum_{l=r}^k\frac{1}{(k-l)!}\, \frac{\partial^{2l+1}g(0)}{(2l+1)!}\,v^{2k+1}e^{-v^2}\in\mathcal{S}_{r}(\mathbb{R}). \end{align*}$$
By (6.4), condition (6.9) is valid for
![]() $a_{n-1}(g)$
. By Lemma 6.2,
$a_{n-1}(g)$
. By Lemma 6.2,
![]() $g-a_{n-1}(g)\in \mathcal {S}_n(\mathbb {R})$
. In light of (6.8),
$g-a_{n-1}(g)\in \mathcal {S}_n(\mathbb {R})$
. In light of (6.8),
![]() $v^{2n}\mathcal {F}_{r}^{\lambda }(g-a_{n-1}(g))(v)$
is the
$v^{2n}\mathcal {F}_{r}^{\lambda }(g-a_{n-1}(g))(v)$
is the
![]() $\mathcal {F}_{r}^{\lambda }$
-transform of the function
$\mathcal {F}_{r}^{\lambda }$
-transform of the function
![]() $(-1)^n\delta _{\lambda }^n(g-a_{n-1}(g))\in \mathcal {S}(\mathbb {R})$
. Applying for this transform inequality (6.2), we get the property (6.9) for
$(-1)^n\delta _{\lambda }^n(g-a_{n-1}(g))\in \mathcal {S}(\mathbb {R})$
. Applying for this transform inequality (6.2), we get the property (6.9) for
![]() $g-a_{n-1}(g)$
. Therefore,
$g-a_{n-1}(g)$
. Therefore,
![]() $\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}(\mathbb {R})$
. By virtue of (6.1) and (6.3),
$\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}(\mathbb {R})$
. By virtue of (6.1) and (6.3),
![]() $\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}_{r}(\mathbb {R})$
.
$\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}_{r}(\mathbb {R})$
.
Remark 6.4. An alternative proof of Proposition 6.3 reads as follows. Let
![]() $g\in \mathcal {S}_{r}(\mathbb {R})$
. In light of (5.1)–(5.3), we have the following representation
$g\in \mathcal {S}_{r}(\mathbb {R})$
. In light of (5.1)–(5.3), we have the following representation
 $$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)&=\int_{-\infty}^{\infty}j_{\lambda}(uv)g(u)\,d\widetilde{\nu}_{\lambda}(u)+ \frac{i(-1)^{r+1}v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\int_{-\infty}^{\infty}u^{2r+1}j_{\lambda+2r+1}(uv)g(u)\,d\widetilde{\nu}_{\lambda}(u)\\ &=\int_{0}^{\infty}j_{\lambda}(uv)g_{e}(u)\,d\nu_{\lambda}(u)+i(-1)^{r+1}v^{2r+1}\int_{0}^{\infty}j_{\lambda+2r+1}(uv)u^{-(2r+1)}g_{o}(u) \,d\nu_{\lambda+2r+1}(u)\\ &=H_{\lambda}(g_e)(v)++i(-1)^{r+1}v^{2r+1}H_{\lambda+2r+1}(u^{-(2r+1)}g_o)(v) =F_1(v)+v^{2r+1}F_2(v), \end{align*} $$
$$ \begin{align*} \mathcal{F}_{r}^{\lambda}(g)(v)&=\int_{-\infty}^{\infty}j_{\lambda}(uv)g(u)\,d\widetilde{\nu}_{\lambda}(u)+ \frac{i(-1)^{r+1}v^{2r+1}}{2^{2r+1}(\lambda+1)_{2r+1}}\int_{-\infty}^{\infty}u^{2r+1}j_{\lambda+2r+1}(uv)g(u)\,d\widetilde{\nu}_{\lambda}(u)\\ &=\int_{0}^{\infty}j_{\lambda}(uv)g_{e}(u)\,d\nu_{\lambda}(u)+i(-1)^{r+1}v^{2r+1}\int_{0}^{\infty}j_{\lambda+2r+1}(uv)u^{-(2r+1)}g_{o}(u) \,d\nu_{\lambda+2r+1}(u)\\ &=H_{\lambda}(g_e)(v)++i(-1)^{r+1}v^{2r+1}H_{\lambda+2r+1}(u^{-(2r+1)}g_o)(v) =F_1(v)+v^{2r+1}F_2(v), \end{align*} $$
where even functions
![]() $F_1,F_2\in \mathcal {S}(\mathbb {R})$
. Therefore,
$F_1,F_2\in \mathcal {S}(\mathbb {R})$
. Therefore,
![]() $\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}_{r}(\mathbb {R})$
. The first proof was given to underline the important properties of
$\mathcal {F}_{r}^{\lambda }(g)\in \mathcal {S}_{r}(\mathbb {R})$
. The first proof was given to underline the important properties of
![]() $\mathcal {F}_{r}^{\lambda }$
-transform and its kernel.
$\mathcal {F}_{r}^{\lambda }$
-transform and its kernel.
Since
![]() $f\in \mathcal {S}(\mathbb {R})$
implies
$f\in \mathcal {S}(\mathbb {R})$
implies
![]() $Af\in \mathcal {S}_r(\mathbb {R})$
, Proposition 6.3 yields the following result.
$Af\in \mathcal {S}_r(\mathbb {R})$
, Proposition 6.3 yields the following result.
Corollary 6.5. Let
![]() $a=\frac {2}{2r+1}$
and
$a=\frac {2}{2r+1}$
and
![]() $\kappa \ge \frac {r}{2r+1}$
. If
$\kappa \ge \frac {r}{2r+1}$
. If
![]() $f\in \mathcal {S}(\mathbb {R})$
, then
$f\in \mathcal {S}(\mathbb {R})$
, then
![]() $\mathcal {F}_{\kappa ,a}(f)((2r+1)^{-(r+1/2)} v^{2r+1})\in \mathcal {S}_r(\mathbb {R})$
or, equivalently,
$\mathcal {F}_{\kappa ,a}(f)((2r+1)^{-(r+1/2)} v^{2r+1})\in \mathcal {S}_r(\mathbb {R})$
or, equivalently,
![]() $\mathcal {F}_{\kappa ,a}(f)(v)=g((2r+1)^{1/2}\,v^{1/(2r+1)})$
,
$\mathcal {F}_{\kappa ,a}(f)(v)=g((2r+1)^{1/2}\,v^{1/(2r+1)})$
,
![]() $g\in \mathcal {S}_r(\mathbb {R})$
; cf. (5.4).
$g\in \mathcal {S}_r(\mathbb {R})$
; cf. (5.4).
Now, we discuss the case
![]() $\lambda =-1/2$
.
$\lambda =-1/2$
.
Remark 6.6. If
![]() $\lambda =-1/2$
,
$\lambda =-1/2$
,
![]() $r\in \mathbb {Z}_+$
, then
$r\in \mathbb {Z}_+$
, then
Taking into account (2.4), and passing to the limit in (2.4) as
![]() $\lambda \to -1/2$
, we deduce that for
$\lambda \to -1/2$
, we deduce that for
![]() $r\ge 1$
$r\ge 1$
 $$ \begin{align*} e_{2r+1}(uv,-1/2)&=\cos{}(uv)+ i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(1/2)_{2r+1}} j_{2r+1/2}(uv)\\ &=e^{-iuv}-(r+1/2)\int_{-1}^{1}\sum_{s=0}^{r-1}(-1)^s\binom{r}{s+1}\frac{(r+3/2)_s}{s!}\,(1-t^2)^ste^{-iuvt}\,dt. \end{align*} $$
$$ \begin{align*} e_{2r+1}(uv,-1/2)&=\cos{}(uv)+ i(-1)^{r+1}\,\frac{(uv)^{2r+1}}{2^{2r+1}(1/2)_{2r+1}} j_{2r+1/2}(uv)\\ &=e^{-iuv}-(r+1/2)\int_{-1}^{1}\sum_{s=0}^{r-1}(-1)^s\binom{r}{s+1}\frac{(r+3/2)_s}{s!}\,(1-t^2)^ste^{-iuvt}\,dt. \end{align*} $$
Taking this into account and analyzing the proofs above, we note that all mentioned results in this section for the transform
![]() $\mathcal {F}_{r}^{\lambda }$
in the case
$\mathcal {F}_{r}^{\lambda }$
in the case
![]() $\lambda>-1/2$
are also valid for
$\lambda>-1/2$
are also valid for
![]() $\lambda =-1/2$
. In particular,
$\lambda =-1/2$
. In particular,
![]() $\mathcal {F}_{r}^{-1/2}$
,
$\mathcal {F}_{r}^{-1/2}$
,
![]() $r\in \mathbb {Z}_+$
, are the unitary transforms in the nonweighted
$r\in \mathbb {Z}_+$
, are the unitary transforms in the nonweighted
![]() $L^2(\mathbb {R},dx)$
, where
$L^2(\mathbb {R},dx)$
, where
![]() $\mathcal {F}_{0}^{-1/2}$
corresponds to the classical Fourier transform.
$\mathcal {F}_{0}^{-1/2}$
corresponds to the classical Fourier transform.
Acknowledgements
We would like to thank the unknown referees for their valuable comments and suggestions which helped to improve the paper. The research of D. Gorbachev and V. Ivanov was performed by a grant of RSF (project 18-11-00199), https://rscf.ru/project/18-11-00199. S. Tikhonov was partially supported by PID2020-114948GB-I00, 2021 SGR 00087, the CERCA Programme of the Generalitat de Catalunya, Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (CEX2020-001084-M), and the Ministry of Education and Science of the Republic of Kazakhstan (AP 14870758).
Competing interest
The authors have no competing interest to declare.