Research Article
Some problems of non-associative combinations (I)
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. i-vi
-
- Article
-
- You have access
- Export citation
Some problems of non-associative combinations (2)
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. vii-xii
-
- Article
-
- You have access
- Export citation
On the evaluation of
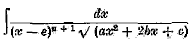
-
- Published online by Cambridge University Press:
- 18 April 2016, pp. xiii-xiv
-
- Article
-
- You have access
- Export citation
A dual quadratic transformation associated with the Hessian conics of a pencil
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xiv-xvi
-
- Article
-
- You have access
- Export citation
Collapsible circular sections of quadric surfaces
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xvi-xix
-
- Article
-
- You have access
- Export citation
Note on an alternant suggested by statistical theory
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xix-xxii
-
- Article
-
- You have access
- Export citation
Maxima and minima
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xxii-xxiii
-
- Article
-
- You have access
- Export citation
On certain modular determinants
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xxiii-xxx
-
- Article
-
- You have access
- Export citation
Inequalities for Positive Series
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xxx-xxxii
-
- Article
-
- You have access
- Export citation
Front matter
MAN volume 32 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 April 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation

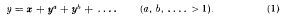
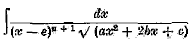
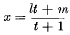 , used to reduce the integral
, used to reduce the integral
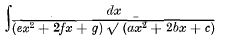
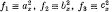 have a symmetrical invariant Ω
have a symmetrical invariant Ω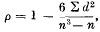 , taken by the product moment correlation coefficient in the special case where the two variables are separate arrangements of the first
, taken by the product moment correlation coefficient in the special case where the two variables are separate arrangements of the first 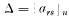
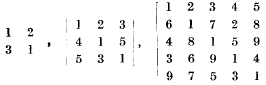 (2) respectively, and their values are
(2) respectively, and their values are