No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 31 October 2008
1. The invariants and covariants of a system of two conics have been much studied2 but little has been said about those of three conies. Three conics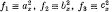 
have a symmetrical invariant Ω123, or in symbolical notation (a b c)2. According to Ciamberlini3 the vanishing of this invariant signifies that the Φ conic of any two of f1, f2, f3 is inpolar with respect to the third; and in a previous paper4 I have derived by symbolical methods a more symmetrical result, viz., if Ω123 vanishes, then u being any line in the plane, u1, u2, u3 are concurrent, where ui is the polar with respect to fi of the pole of u with respect to Φjk.
1 The integral 
is a case in point.
2 See Salmon Conic Sections, Ch. xviii, or Sommerville, Analytical Conies, Ch. xx. Taking point-coordinates x, y, z with corresponding line-coordinates l, m, n, a conic 
has a tangential equation 
. Then the vanishing of the invariant 
of the conics 
implies that there are triangles circumscribed to f 1 which are self-polar for f 2, and f 1 is said to be inpolar to f 2. The contravariant conic Φ12 is the envelope of a line whose intersections with f 1 harmonically separate its intersections with f 2.
3 Giorn. di Mat., Napoli, 32 (1886), 141.Google Scholar
4 Proc. Ed. Math. Soc, 2 iv (1935) 258.Google Scholar
1 Sommerville, loc. cit., p. 278Google Scholar; for a fuller discussion of mutual apolarity, see Strazzeri, , Rend. Circ. Mat. di Palermo, 32 (1937), 100.Google Scholar
You have
Access