Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T01:58:43.470Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain modular determinants

Published online by Cambridge University Press:  31 October 2008

H. W. Turnbull
H. W. Turnbull
Affiliation:
The University, St Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An interesting determinant occurs in the fifth volume of Muir's History1. It is

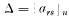
where n = ½ (p – 1), and ars is the smallest positive integer such that

rars = s (mod p), (1) p being any odd prime number. It is evident that each element ars is unique and non zero. For p = 5, 7, 11 the determinants are

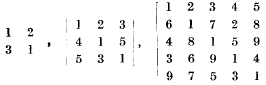(2) respectively, and their values are

– 5 , 72, 114.

Type
Research Article
Information
Edinburgh Mathematical Notes , Volume 32 , January 1940 , pp. xxiii - xxx
Copyright
Copyright © Edinburgh Mathematical Society 1940

References

1 SirMuir, Thomas, The History of Determinants, 1900–1920 (Blackie, 1930), p. 340.Google Scholar Question 4269. L'Intermédiaire des Math., 32 (1913), p. 218Google Scholar, proposed by E. Maillet: reply by E. Malo, 21, pp. 173–176.