Articles
Local and Global Testing of Linear and Nonlinear Inequality Constraints in Nonlinear Econometric Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 1-35
-
- Article
- Export citation
Asymptotic Properties of the Maximum-Likelihood and Nonlinear Least-Squares Estimators for Noninvertible Moving Average Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 333-353
-
- Article
- Export citation
Partially Identified Econometric Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 181-240
-
- Article
- Export citation
The Calculation of the Limiting Distribution of the Least-Squares Estimator in a Near-Integrated Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 241-255
-
- Article
- Export citation
Mirror-Image and Invariant Distributions in ARMA Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 36-52
-
- Article
- Export citation
On the First-Order Autoregressive Process with Infinite Variance
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 354-362
-
- Article
- Export citation
Effect of Nonnormality on the Estimation of a Single Structural Equation with Structural Change
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 53-62
-
- Article
- Export citation
Testing for Unit Roots in Time Series Data
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 256-271
-
- Article
- Export citation
Testing for Consistency using Artificial Regressions
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 363-384
-
- Article
- Export citation
A General Framework for Testing a Null Hypothesis in a “Mixed” Form
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 63-82
-
- Article
- Export citation
Ancillarity and the Limited Information Maximum-Likelihood Estimation of a Structural Equation in a Simultaneous Equation System
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 385-404
-
- Article
- Export citation
Consistency Via Type 2 Inequalities: A Generalization of Wu's Theorem
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 272-286
-
- Article
- Export citation
Et Interview
Interviewed by Peter E. Rossi
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 287-317
-
- Article
- Export citation
Articles
Some Power Comparisons of Joint and Paired Tests for Nonnested Models under Local Hypotheses
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 83-94
-
- Article
- Export citation
On Rereading Haavelmo: A Retrospective View of Econometric Modeling
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 405-429
-
- Article
- Export citation
Predictors in Dynamic Nonlinear Models: Large-Sample Behavior
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 430-452
-
- Article
- Export citation
Statistical Inference in Regressions with Integrated Processes: Part 2
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 95-131
-
- Article
- Export citation
Problems
A Switching Regression Model with Imperfect Sample Separation and Several Regimes
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 319
-
- Article
- Export citation
The Asymptotic Distribution of the Iterated Gauss-Newton Estimators of an ARIMA Process
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 453
-
- Article
- Export citation
Unbiased Prediction in a Simple Simultaneous Equations Model
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 320
-
- Article
- Export citation

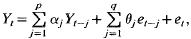 for
for 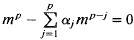 satisfy the hypothesis
satisfy the hypothesis