Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T00:34:55.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Testing for Unit Roots in Time Series Data

Published online by Cambridge University Press:  18 October 2010

Sastry G. Pantula
Sastry G. Pantula
Affiliation:
North Carolina State University
Get access Rights & Permissions [Opens in a new window]

Abstract

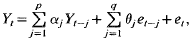Let Yt satisfy the stochastic difference equation for t = 1,2,…, where et are independent and identically distributed random variables with mean zero and variance σ2 and the initial conditions (Y−p+1,…, Y0) are fixed constants. It is assumed that the process is invertible and that the true, but unknown, roots m1,m2,…,mp of 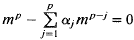satisfy the hypothesis Hd: m1 = … = md = 1 and |mj| < 1 for j = d + 1,…,p. We present a reparameterization of the model for Yt that is convenient for testing the hypothesis Hd. We consider the asymptotic properties of (i) a likelihood ratio type “F-statistic” for testing the hypothesis Hd, (ii) a likelihood ratio type t-statistic for testing the hypothesis Hd against the alternative Hd−1. Using these asymptotic results, we obtain two sequential testing procedures that are asymptotically consistent.

Type
Articles
Information
Econometric Theory , Volume 5 , Issue 2 , August 1989 , pp. 256 - 271
Copyright
Copyright © Cambridge University Press 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Altonji, J. & Ashenfelter, O.. Wage movements and the labor market equilibrium hypothesis. Economica 47 (1980): 217–245.CrossRefGoogle Scholar
2.Anderson, T.W.The statistical analysis of time series. New York: John Wiley and Sons, 1971.Google Scholar
3.Berk, K.N.Consistent autoregressive spectral estimates. The Annals of Statistics 2 (1974): 489–502.CrossRefGoogle Scholar
4.Box, G.E.P. & Pallesen, L.. Adaptive minimum mean square error forecast of missile trajectory using stochastic difference equation models. MRC Technical Summary Report No. 1821, University of Wisconsin, Madison, WI, 1978.Google Scholar
5.Chan, N.H. & Wei, C.Z.. Limiting distributions of least-squares estimates of unstable autoregressive processes. The Annals of Statistics 16 (1988): 367–401.CrossRefGoogle Scholar
6.Dickey, D.A. & Fuller, W.A.. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74 (1979): 427–431.Google Scholar
7.Dickey, D.A. & Pantula, S.G.. Determining the order of differencing in autoregressive processes. Journal of Business and Economic Statistics 5 (1987): 455–461.Google Scholar
8.Fuller, W.A.Introduction to statistical time series. New York: John Wiley & Sons, 1976.Google Scholar
9.Fuller, W.A.Testing the autoregressive process for a unit root. Proceedings of the 42nd Session of the International Statistical Institute, Manilla, Spain, 1979.Google Scholar
10.Hannan, E.J. & Heyde, C.C.. On limit theorems for quadratic functions of discrete time series. Annals of Mathematical Statistics 43 (1972): 2058–2066.CrossRefGoogle Scholar
11.Hasza, D.P. & Fuller, W.A.. Estimation for autoregressive processes with unit roots. Annals of Statistics 7 (1979): 1106–1120.CrossRefGoogle Scholar
12.Lai, T.L. & Wei, C.Z.. Asymptotic properties of general autoregressive models and strong consistency of least-squares estimates of their parameters. Journal of Multivariate Analysis 13 (1983): 1–23.CrossRefGoogle Scholar
13.Mann, H.B. & Wald, A.. On the statistical treatment of linear stochastic difference equations. Econometrica 11 (1943): 173–220.CrossRefGoogle Scholar
14.Meese, R.A. & Singleton, K.J.. On unit roots and the empirical modeling of exchange rates. International Economic Review 24 (1983): 1029–1035.Google Scholar
15.Nelson, C.R. & Plosser, C.I.. Trends and random walks in macroeconomic time series: some evidence and implications. Journal of Monetary Economics 10 (1982): 139–162.CrossRefGoogle Scholar
16.Pantula, S.G.Estimation for autoregressive processes with several unit roots. Institute of Statistics Mimeograph Series No. 1665, North Carolina State University, Raleigh, NC, 1985.Google Scholar
17.Pantula, S.G.Testing for unit roots in time series data. Institute of Statistics Mimeograph Series No. 1903, North Carolina State University, Raleigh, NC, 1987.Google Scholar
18.Phillips, P.C.B.Time series regression with unit roots. Econometrica 55 (1987): 277–302.CrossRefGoogle Scholar
19.Phillips, P.C.B. & Perron, P.. Testing for a unit root in time series regression. Biometrika 75 (1988): 335–346.CrossRefGoogle Scholar
20.Said, S.E. & Dickey, D.A.. Testing for unit roots in autoregressive moving average models of unknown order. Biometrika 71 (1984): 599–607.CrossRefGoogle Scholar
21.Schwert, G.W.Effects of model specification on tests for unit roots in macroeconomic data. Technical Report, University of Rochester, NY, 1987.CrossRefGoogle Scholar
22.Searle, S.R.Linear models. New York: John Wiley and Sons, 1971.Google Scholar
23.Sen, D.L. Robustness of single unit root test statistics in the presence of multiple unit roots. Ph.D. Thesis, North Carolina State University, Raleigh, NC, 1985.Google Scholar
24.Tiao, G.C. & Tsay, R.S.. Consistency properties of least-squares estimates of autoregressive parameters in ARIMA models. Annals of Statistics 11 (1983): 856–871.CrossRefGoogle Scholar
25.Yajima, Y., Estimation of the degree of differencing of an ARIMA process. Annals of the Institute of Statistical Mathematics (Part A) 37 (1985): 387–408.Google Scholar