We study minimax regret treatment rules under matched treatment assignment in a setup where a policymaker, informed by a sample of size N, needs to decide between T different treatments for a 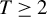 $T\geq 2$. Randomized rules are allowed for. We show that the generalization of the minimax regret rule derived in Schlag (2006, ELEVEN—Tests needed for a recommendation, EUI working paper) and Stoye (2009, Journal of Econometrics 151, 70–81) for the case
$T\geq 2$. Randomized rules are allowed for. We show that the generalization of the minimax regret rule derived in Schlag (2006, ELEVEN—Tests needed for a recommendation, EUI working paper) and Stoye (2009, Journal of Econometrics 151, 70–81) for the case  $T=2$ is minimax regret for general finite
$T=2$ is minimax regret for general finite 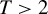 $T>2$ and also that the proof structure via the Nash equilibrium and the “coarsening” approaches generalizes as well. We also show by example, that in the case of random assignment the generalization of the minimax rule in Stoye (2009, Journal of Econometrics 151, 70–81) to the case
$T>2$ and also that the proof structure via the Nash equilibrium and the “coarsening” approaches generalizes as well. We also show by example, that in the case of random assignment the generalization of the minimax rule in Stoye (2009, Journal of Econometrics 151, 70–81) to the case 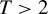 $T>2$ is not necessarily minimax regret and derive minimax regret rules for a few small sample cases, e.g., for
$T>2$ is not necessarily minimax regret and derive minimax regret rules for a few small sample cases, e.g., for 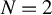 $N=2$ when
$N=2$ when 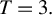 $T=3.$
$T=3.$
In the case where a covariate x is included, it is shown that a minimax regret rule is obtained by using minimax regret rules in the “conditional-on-x” problem if the latter are obtained as Nash equilibria.