Articles
A Unified Theory of Consistent Estimation for Parametric Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 151-178
-
- Article
- Export citation
On Differentiating Eigenvalues and Eigenvectors
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 179-191
-
- Article
- Export citation
A Theory of Serial Correlation of Stochastic Taste Changers in Direct Utility Functions
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 192-210
-
- Article
- Export citation
A Point Optimal Test for Moving Average Regression Disturbances
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 211-222
-
- Article
- Export citation
Edgeworth Expansion for the OLS Estimator in a Time Series Regression Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 223-239
-
- Article
- Export citation
Improving Some Instrumental Variables Test Procedures
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 240-262
-
- Article
- Export citation
Et Interviews
Proffessor E. J. Hannnan
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 263-290
-
- Article
- Export citation
Problems and Solutions
Efficient Reduced Form Estimation via OLS
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 291-292
-
- Article
- Export citation
Distribution of F-ratio
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 292-293
-
- Article
- Export citation
Prediction Error Variances under Heteroscedasticity
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 293-294
-
- Article
- Export citation
Estimation of a Constrained Equation System
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 294
-
- Article
- Export citation
Front matter
ECT volume 1 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

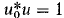 . We investigate the conditions under which unique differentiable functions λ(
. We investigate the conditions under which unique differentiable functions λ(