Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T19:10:19.121Z Has data issue: false hasContentIssue false
  • English
  • Français

On Differentiating Eigenvalues and Eigenvectors

Published online by Cambridge University Press:  18 October 2010

Jan R. Magnus
Jan R. Magnus
Affiliation:
London School of Economics
Get access Rights & Permissions [Opens in a new window]

Abstract

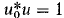Let X0 be a square matrix (complex or otherwise) and u0 a (normalized) eigenvector associated with an eigenvalue λo of X0, so that the triple (X0, u0, λ0) satisfies the equations Xu = λu, . We investigate the conditions under which unique differentiable functions λ(X) and u(X) exist in a neighborhood of X0 satisfying λ(X0) = λO, u(X0) = u0, Xu = λu, and 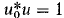. We obtain the first and second derivatives of λ(X) and the first derivative of u(X). Two alternative expressions for the first derivative of λ(X) are also presented.

Type
Articles
Information
Econometric Theory , Volume 1 , Issue 2 , August 1985 , pp. 179 - 191
Copyright
Copyright © Cambridge University Press 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Bargmann, R. E. and Nel, D. G.. On the matrix differentiation of the characteristic roots of matrices. South African Statistical Journal 8 (1974): 135–144.Google Scholar
2.Lancaster, P.On eigenvalues of matrices dependent on a parameter. Numerische Mathematik 6 (1964): 377–387.CrossRefGoogle Scholar
3.Magnus, J. R. and Neudecker, H.. The commutation matrix: Some properties and applications. The Annals of Statistics 7 (1979): 381–394.CrossRefGoogle Scholar
4.Magnus, J. R. and Neudecker, H.. The elimination matrix: Some lemmas and applications. SIAM Journal on Algebraic and Discrete Methods 1 (1980): 422–449.CrossRefGoogle Scholar
5.Neudecker, H.On matrix procedures for optimizing differentiable scalar functions of matrices. Statistica Neerlandica 21 (1967): 101–107.CrossRefGoogle Scholar
6.Phillips, P.C.B.A simple proof of the latent root sensitivity formula. Economics Letters 9 (1982): 57–59.CrossRefGoogle Scholar
7.Sugiura, N.Derivatives of the characteristic root of a symmetric or a hermitian matrix with two applications in multivariate analysis. Communications in Statistics 1 (1973): 393–417.CrossRefGoogle Scholar