Let 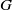$G$ be a connected, reductive algebraic group over a number field 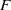$F$ and let 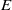$E$ be an algebraic representation of 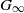${G}_{\infty } $. In this paper we describe the Eisenstein cohomology 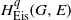${ H}_{\mathrm{Eis} }^{q} (G, E)$ of 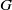$G$ below a certain degree 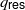${q}_{ \mathsf{res} } $ in terms of Franke’s filtration of the space of automorphic forms. This entails a description of the map 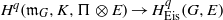${H}^{q} ({\mathfrak{m}}_{G} , K, \Pi \otimes E)\rightarrow { H}_{\mathrm{Eis} }^{q} (G, E)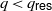$, $q\lt {q}_{ \mathsf{res} } $, for all automorphic representations 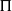$\Pi $ of 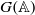$G( \mathbb{A} )$ appearing in the residual spectrum. Moreover, we show that below an easily computable degree 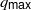${q}_{ \mathsf{max} } $, the space of Eisenstein cohomology 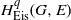${ H}_{\mathrm{Eis} }^{q} (G, E)$ is isomorphic to the cohomology of the space of square-integrable, residual automorphic forms. We discuss some more consequences of our result and apply it, in order to derive a result on the residual Eisenstein cohomology of inner forms of 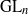${\mathrm{GL} }_{n} $ and the split classical groups of type 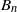${B}_{n} 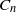$, ${C}_{n} 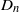$, ${D}_{n} $.

Let $K$ be a finitely generated extension of $\mathbb {Q}$. We consider the family of $\ell $-adic representations ($\ell $ varies through the set of all prime numbers) of the absolute Galois group of $K$, attached to $\ell $-adic cohomology of a separated scheme of finite type over $K$. We prove that the fields cut out from the algebraic closure of $K$by the kernels of the representations of the family are linearly disjoint over a finite extension of K. This gives a positive answer to a question of Serre.

Let $ \mathcal{X} $ be a curve over ${ \mathbb{F} }_{q} $ and let $N( \mathcal{X} )$, $g( \mathcal{X} )$ be its number of rational points and genus respectively. The Ihara constant $A(q)$ is defined by $A(q)= {\mathrm{lim~sup} }_{g( \mathcal{X} )\rightarrow \infty } N( \mathcal{X} )/ g( \mathcal{X} )$. In this paper, we employ a variant of Serre’s class field tower method to obtain an improvement of the best known lower bounds on $A(2)$ and $A(3)$.

Building on the concept of pretentious multiplicative functions, we give a new and largely elementary proof of the best result known on the counting function of primes in arithmetic progressions.

Let $q$ be a prime and $- D\lt - 4$ be an odd fundamental discriminant such that $q$ splits in $ \mathbb{Q} ( \sqrt{- D} )$. For $f$ a weight-zero Hecke–Maass newform of level $q$ and ${\Theta }_{\chi } $ the weight-one theta series of level $D$ corresponding to an ideal class group character $\chi $ of $ \mathbb{Q} ( \sqrt{- D} )$, we establish a hybrid subconvexity bound for $L(f\times {\Theta }_{\chi } , s)$ at $s= 1/ 2$ when $q\asymp {D}^{\eta } $ for $0\lt \eta \lt 1$. With this circle of ideas, we show that the Heegner points of level $q$ and discriminant $D$ become equidistributed, in a natural sense, as $q, D\rightarrow \infty $ for $q\leq {D}^{1/ 20- \varepsilon } $. Our approach to these problems is connected to estimating the ${L}^{2} $-restriction norm of a Maass form of large level $q$ when restricted to the collection of Heegner points. We furthermore establish bounds for quadratic twists of Hecke–Maass $L$-functions with simultaneously large level and large quadratic twist, and hybrid bounds for quadratic Dirichlet $L$-functions in certain ranges.

Let $N/ F$ be an odd-degree Galois extension of number fields with Galois group $G$ and rings of integers ${\mathfrak{O}}_{N} $ and ${\mathfrak{O}}_{F} = \mathfrak{O}$. Let $ \mathcal{A} $ be the unique fractional ${\mathfrak{O}}_{N} $-ideal with square equal to the inverse different of $N/ F$. B. Erez showed that $ \mathcal{A} $ is a locally free $\mathfrak{O}[G] $-module if and only if $N/ F$ is a so-called weakly ramified extension. Although a number of results have been proved regarding the freeness of $ \mathcal{A} $ as a $ \mathbb{Z} [G] $-module, the question remains open. In this paper we prove that $ \mathcal{A} $ is free as a $ \mathbb{Z} [G] $-module provided that $N/ F$ is weakly ramified and under the hypothesis that for every prime $\wp $ of $\mathfrak{O}$ which ramifies wildly in $N/ F$, the decomposition group is abelian, the ramification group is cyclic and $\wp $ is unramified in $F/ \mathbb{Q} $. We make crucial use of a construction due to the first author which uses Dwork’s exponential power series to describe self-dual integral normal bases in Lubin–Tate extensions of local fields. This yields a new and striking relationship between the local norm-resolvent and the Galois Gauss sum involved. Our results generalise work of the second author concerning the case of base field $ \mathbb{Q} $.

Let $\mathfrak{a}$ be a homogeneous ideal of a polynomial ring $R$ in $n$ variables over a field $\mathbb{k}$. Assume that $\mathrm{depth} (R/ \mathfrak{a})\geq t$, where $t$ is some number in $\{ 0, \ldots , n\} $. A result of Peskine and Szpiro says that if $\mathrm{char} (\mathbb{k})\gt 0$, then the local cohomology modules ${ H}_{\mathfrak{a}}^{i} (M)$ vanish for all $i\gt n- t$ and all $R$-modules $M$. In characteristic $0$, there are counterexamples to this for all $t\geq 4$. On the other hand, when $t\leq 2$, by exploiting classical results of Grothendieck, Lichtenbaum, Hartshorne and Ogus it is not difficult to extend the result to any characteristic. In this paper we settle the remaining case; specifically, we show that if $\mathrm{depth} (R/ \mathfrak{a})\geq 3$, then the local cohomology modules ${ H}_{\mathfrak{a}}^{i} (M)$ vanish for all $i\gt n- 3$ and all $R$-modules $M$, whatever the characteristic of $\mathbb{k}$ is.

We show that the automorphism group of Drinfeld’s half-space over a finite field is the projective linear group of the underlying vector space. The proof of this result uses analytic geometry in the sense of Berkovich over the finite field equipped with the trivial valuation. We also take into account extensions of the base field.

We prove that the quotient by ${\mathrm{SL} }_{2} \times {\mathrm{SL} }_{2} $ of the space of bidegree $(a, b)$ curves on ${ \mathbb{P} }^{1} \times { \mathbb{P} }^{1} $ is rational when $ab$ is even and $a\not = b$.