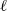Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-03T01:19:34.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Independence of $\ell $-adic Galois representations over function fields

Part of: Arithmetic algebraic geometry (Co)homology theory

Published online by Cambridge University Press:  25 April 2013

Wojciech Gajda  and
Sebastian Petersen
Wojciech Gajda
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61614 Poznań, Poland (email: [email protected])
Sebastian Petersen
Affiliation:
FB 10 - Mathematik und Naturwissenschaften, Universität Kassel, Heinrich-Plett-Str. 40, 34132 Kassel, Germany (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 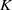$K$ be a finitely generated extension of 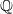$\mathbb {Q}$. We consider the family of 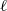$\ell $-adic representations (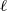$\ell $ varies through the set of all prime numbers) of the absolute Galois group of 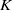$K$, attached to 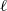$\ell $-adic cohomology of a separated scheme of finite type over 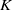$K$. We prove that the fields cut out from the algebraic closure of 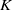$K$by the kernels of the representations of the family are linearly disjoint over a finite extension of K. This gives a positive answer to a question of Serre.

Keywords

Galois representationétale cohomologyabelian varietyfinitely generated field

MSC classification

Secondary: 11G10: Abelian varieties of dimension $> 1$ 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 7 , July 2013 , pp. 1091 - 1107
Copyright
Copyright © 2013 The Author(s) 

References

[Art55]Artin, E., The orders of the classical simple groups, Comm. Pure Appl. Math. 8 (1955), 455–472.Google Scholar
[EGAII]Grothendieck, A., Éléments de géométrie algébrique (rédigé avec la cooperation de Jean Dieudonné): II. Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Études Sci. 8 (1961), 5–222.Google Scholar
[EGAIV3]Grothendieck, A., Éléments de géométrie algébrique (rédigé avec la cooperation de Jean Dieudonné): IV. Étude locale des schémas et des morphismes des schémas, Troisième partie, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.Google Scholar
[FJ05]Fried, M. D. and Jarden, M., Field arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11, 2nd revised and enlarged ed (Springer, Berlin, 2005).Google Scholar
[Ill]Illusie, L., Constructibilité générique et uniformité en $\ell $, Preprint.Google Scholar
[KL81]Katz, N. and Lang, S., Finiteness theorems in geometric class field theory, Enseign. Math. 27 (1981), 285–319.Google Scholar
[KL86]Katz, N. and Laumon, G., Transformation de Fourier et majoration de sommes exponentielles, Publ. Math. Inst. Hautes Études Sci. 62 (1986), 361–418. Erratum: Publ. Math. Inst. Hautes Études Sci. 69 (1989), 244.Google Scholar
[KLST90]Kimmerle, W., Lyons, R., Sandling, R. and Teague, D., Composition factors from the group ring and Artin’s theorem on orders of simple groups, Proc. Lond. Math. Soc. 60 (1990), 89–122.Google Scholar
[Mil80]Milne, J., Étale cohomology (Princeton University Press, New Jersey, 1980).Google Scholar
[Nor87]Nori, M., On subgroups of $GL_n(\mathbb {F}_p)$, Invent. Math. (1987), 257–275.Google Scholar
[Ser94]Serre, J.-P., Propriétés conjecturales des groupes de Galois motiviques et des représentations $\ell $-adiques, Proc. Sympos. Pure Math. (1994), 377–400.Google Scholar
[Ser00]Serre, J.-P., Lettre à Ken Ribet du 7/3/1986, in Œuvres. Collected papers, IV, 1985–1998 (Springer, Berlin, 2000).Google Scholar
[Ser10]Serre, J.-P., Une critère d’indépendance pour une famille de représentations $\ell $-adiques, Preprint (2010), available at arXiv:1006.2442.Google Scholar
[SGA4]Artin, M., Grothendieck, A. and Verdier, J.-L., Séminaire de Géomt́rie Algébrique du Bois Marie 1963–64 - Théorie des topos et cohomologie étale des schémas (SGA 4), Lecture Notes in Mathematics, vol. 269, 270, 305 (Springer, 1972).Google Scholar
[SGA7]Grothendieck, A., Séminaire de Géométrie Algébrique du Bois Marie 1967–69 - Groupes de monodromy en géométrie algébrique (SGA 7), vol. 1, Lecture Notes in Mathematics, vol. 288 (Springer, Berlin, 1972).Google Scholar