Let \mathbb {V}$\mathbb {V}$ be a polarized variation of Hodge structure over a smooth complex quasi-projective variety S$S$. In this paper, we give a complete description of the typical Hodge locus for such variations. We prove that it is either empty or equidistributed with respect to a natural differential form, the pull–push form. In particular, it is always analytically dense when the pull–push form does not vanish. When the weight is two, the Hodge numbers are (q,p,q)$(q,p,q)$ and the dimension of S$S$ is least rq$rq$, we prove that the typical locus where the Picard rank is at least r$r$ is equidistributed in S$S$ with respect to the volume form c_q^r$c_q^r$, where c_q$c_q$ is the q$q$th Chern form of the Hodge bundle. We obtain also several equidistribution results of the typical locus in Shimura varieties: a criterion for the density of the typical Hodge loci of a variety in \mathcal {A}_g$\mathcal {A}_g$, equidistribution of certain families of CM points and equidistribution of Hecke translates of curves and surfaces in \mathcal {A}_g$\mathcal {A}_g$. These results are proved in the much broader context of dynamics on homogeneous spaces of Lie groups which are of independent interest. The pull–push form appears in this greater generality, we provide several tools to determine it, and we compute it in many examples.

We prove an analogue of Lang's conjecture on divisible groups for polynomial dynamical systems over number fields. In our setting, the role of the divisible group is taken by the small orbit of a point 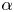\alpha$\alpha$ where the small orbit by a polynomial 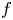f$f$ is given by

Our main theorem is a classification of the algebraic relations that hold between infinitely many pairs of points in 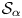\mathcal {S}_\alpha$\mathcal {S}_\alpha$ when everything is defined over the algebraic numbers and the degree 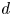d$d$ of 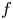f$f$ is at least 2. Our proof relies on a careful study of localisations of the dynamical system and follows an entirely different approach than previous proofs in this area. In particular, we introduce transcendence theory and Mahler functions into this field. Our methods also allow us to classify all algebraic relations that hold for infinitely many pairs of points in the grand orbit

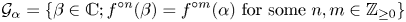\begin{align*} \mathcal{G}_\alpha = \{\beta \in \mathbb{C}; f^{\circ n}(\beta) = f^{\circ m}(\alpha) \text{ for some } n ,m\in \mathbb{Z}_{\geq 0}\} \end{align*} $$\begin{align*} \mathcal{G}_\alpha = \{\beta \in \mathbb{C}; f^{\circ n}(\beta) = f^{\circ m}(\alpha) \text{ for some } n ,m\in \mathbb{Z}_{\geq 0}\} \end{align*}$$

of 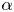\alpha$\alpha$ if 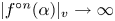|f^{\circ n}(\alpha )|_v \rightarrow \infty$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place 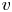v$v$ of good reduction co-prime to 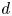d$d$.

We prove an extension of the homology version of the Hofer–Zehnder conjecture proved by Shelukhin to the weighted projective spaces which are symplectic orbifolds. In particular, we prove that if the number of fixed points counted with their isotropy order as multiplicity of a non-degenerate Hamiltonian diffeomorphism of such a space is larger than the minimum number possible, then there are infinitely many periodic points.

We introduce a linearised form of the square root of the Todd class inside the Verbitsky component of a hyper-Kähler manifold using the extended Mukai lattice. This enables us to define a Mukai vector for certain objects in the derived category taking values inside the extended Mukai lattice which is functorial for derived equivalences. As applications, we obtain a structure theorem for derived equivalences between hyper-Kähler manifolds as well as an integral lattice associated to the derived category of hyper-Kähler manifolds deformation equivalent to the Hilbert scheme of a K3 surface mimicking the surface case.

Given a finitely generated free group {\mathbb {F} }${\mathbb {F} }$ of \mathsf {rank}( {\mathbb {F} } )\geq 3$\mathsf {rank}( {\mathbb {F} } )\geq 3$, we show that the mapping torus of \phi$\phi$ is (strongly) relatively hyperbolic if \phi$\phi$ is exponentially growing. As a corollary of our work, we give a new proof of Brinkmann's theorem which proves that the mapping torus of an atoroidal outer automorphism is hyperbolic. We also give a new proof of the Bridson–Groves theorem that the mapping torus of a free group automorphism satisfies the quadratic isoperimetric inequality. Our work also solves a problem posed by Minasyan and Osin: the mapping torus of an outer automorphism is not virtually acylindrically hyperbolic if and only if \phi$\phi$ has finite order.

For any odd integer d$d$, we give a presentation for the integral Chow ring of the stack \mathcal {M}_{0}(\mathbb {P}^r, d)$\mathcal {M}_{0}(\mathbb {P}^r, d)$, as a quotient of the polynomial ring \mathbb {Z}[c_1,c_2]$\mathbb {Z}[c_1,c_2]$. We describe an efficient set of generators for the ideal of relations, and compute them in generating series form. The paper concludes with explicit computations of some examples for low values of d$d$ and r$r$, and a conjecture for a minimal set of generators.