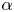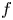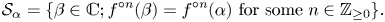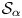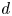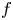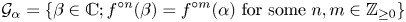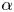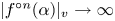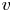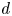1. Introduction
Let ![]() $K$ be a number field and
$K$ be a number field and ![]() $\alpha \in K$. We study the dynamical system attached to a polynomial
$\alpha \in K$. We study the dynamical system attached to a polynomial ![]() $f \in K[X]$ of degree
$f \in K[X]$ of degree ![]() $d \geq 2$ and denote by
$d \geq 2$ and denote by ![]() ${f^{\circ n}}$ the
${f^{\circ n}}$ the ![]() $n$th iterate of
$n$th iterate of ![]() $f$ defined by
$f$ defined by ![]() $f^{\circ 0}(X) = X$ and
$f^{\circ 0}(X) = X$ and ![]() $f^{\circ n}(X) = f^{\circ n-1}(f(X))$ for
$f^{\circ n}(X) = f^{\circ n-1}(f(X))$ for ![]() $n \in \mathbb {Z}_{\geq 1}$. We consider the small orbit
$n \in \mathbb {Z}_{\geq 1}$. We consider the small orbit ![]() $\mathcal {S}_\alpha$ of a point
$\mathcal {S}_\alpha$ of a point ![]() $\alpha$ that was introduced by McMullen and Sullivan [Reference McMullen and SullivanMS98, 6.1] as part of their investigations of the dynamics of holomorphic maps. It is given by
$\alpha$ that was introduced by McMullen and Sullivan [Reference McMullen and SullivanMS98, 6.1] as part of their investigations of the dynamics of holomorphic maps. It is given by
This ![]() $\mathcal {S}_\alpha$ is an infinite set unless
$\mathcal {S}_\alpha$ is an infinite set unless ![]() $\alpha$ is a super-attractive fixed point of degree
$\alpha$ is a super-attractive fixed point of degree ![]() $d$ (see [Reference MilnorMil06] for a definition). In order to have a more traditional diophantine analogue we may consider
$d$ (see [Reference MilnorMil06] for a definition). In order to have a more traditional diophantine analogue we may consider ![]() $\mathcal {S}_\alpha$ to be the set of ‘torsion translates’ of
$\mathcal {S}_\alpha$ to be the set of ‘torsion translates’ of ![]() $\alpha$ for the dynamical system attached to
$\alpha$ for the dynamical system attached to ![]() $f$. For example, in the more classical setting of the multiplicative group
$f$. For example, in the more classical setting of the multiplicative group ![]() $\mathbb {G}_m$ an element
$\mathbb {G}_m$ an element ![]() $x$ of
$x$ of ![]() $\alpha \mu _{\infty }$ (where
$\alpha \mu _{\infty }$ (where ![]() $\mu _{\infty }$ is the group of roots of unity) satisfies
$\mu _{\infty }$ is the group of roots of unity) satisfies ![]() $x^{n} = \alpha ^{n}$ for some positive integer
$x^{n} = \alpha ^{n}$ for some positive integer ![]() $n$. The study of the equation
$n$. The study of the equation ![]() $x^{n} = y^{n}$ where
$x^{n} = y^{n}$ where ![]() $y$ varies in a finitely generated group is integral to go from the Mordellic part to Lang's full conjecture in
$y$ varies in a finitely generated group is integral to go from the Mordellic part to Lang's full conjecture in ![]() $\mathbb {G}_m^{n}$ (see [Reference LaurentLau84]). In fact, by employing Kummer theory one reduces the conjecture to the study of this equation (and, thus, Manin–Mumford with a certain uniformity). The same approach is used in all known proofs of Mordell–Lang to go from the Mordellic part to the divisible hull (for example, in the ultimate resolution of the conjecture for semi-abelian varieties by McQuillan [Reference McQuillanMcQ95]).
$\mathbb {G}_m^{n}$ (see [Reference LaurentLau84]). In fact, by employing Kummer theory one reduces the conjecture to the study of this equation (and, thus, Manin–Mumford with a certain uniformity). The same approach is used in all known proofs of Mordell–Lang to go from the Mordellic part to the divisible hull (for example, in the ultimate resolution of the conjecture for semi-abelian varieties by McQuillan [Reference McQuillanMcQ95]).
In this article, we obtain a structure theorem for the set ![]() $\mathcal {S}_\alpha$ that is analogous to what Manin–Mumford delivers in the context of algebraic groups (and also achieve a certain uniformity). We also use a similar strategy in this context to show, quite analogously as in the group context, that we can go from the small orbit of
$\mathcal {S}_\alpha$ that is analogous to what Manin–Mumford delivers in the context of algebraic groups (and also achieve a certain uniformity). We also use a similar strategy in this context to show, quite analogously as in the group context, that we can go from the small orbit of ![]() $\alpha$ to its grand orbit
$\alpha$ to its grand orbit
albeit under the condition that the orbit of ![]() $\alpha$ tends to infinity at a finite place of good reduction co-prime to
$\alpha$ tends to infinity at a finite place of good reduction co-prime to ![]() $d$. These results may be viewed as new cases of the Zilber–Pink (or unlikely intersection) conjecture on dynamical systems as formulated in [Reference Ghioca and NguyenGN16, p. 1438] as we explain in the following. In order to ease notation and deal with trivial cases and those covered by previous results, we introduce two definitions (one of which appeared previously in the literature).
$d$. These results may be viewed as new cases of the Zilber–Pink (or unlikely intersection) conjecture on dynamical systems as formulated in [Reference Ghioca and NguyenGN16, p. 1438] as we explain in the following. In order to ease notation and deal with trivial cases and those covered by previous results, we introduce two definitions (one of which appeared previously in the literature).
Definition 1 Let ![]() $\mathcal {K}$ be a field and
$\mathcal {K}$ be a field and ![]() $\bar {\mathcal {K}}$ its algebraic closure.
$\bar {\mathcal {K}}$ its algebraic closure.
(i) We say that a curve
 $\mathcal {C} \subset \mathbb {A}^{2}$ defined over a field
$\mathcal {C} \subset \mathbb {A}^{2}$ defined over a field  $\mathcal {K}$ is fibral if it is of the form
$\mathcal {K}$ is fibral if it is of the form  $\mathcal {C} = \{\gamma \}\times \mathbb {A}^{1}$ or
$\mathcal {C} = \{\gamma \}\times \mathbb {A}^{1}$ or  $\mathcal {C} = \mathbb {A}^{1}\times \{\gamma \}$ for
$\mathcal {C} = \mathbb {A}^{1}\times \{\gamma \}$ for  $\gamma \in \mathcal {K}$.
$\gamma \in \mathcal {K}$.(ii) We call a polynomial
 $f$ exceptional if there exists a linear polynomial
$f$ exceptional if there exists a linear polynomial  $L \in \bar {\mathcal {K}}[X]$ such that
$L \in \bar {\mathcal {K}}[X]$ such that  $L\circ f\circ L^{-1}$ is equal to
$L\circ f\circ L^{-1}$ is equal to  $X^{d}$ or to a Chebychev polynomial or a negative Chebychev polynomial. Otherwise, we call a polynomial non-exceptional.
$X^{d}$ or to a Chebychev polynomial or a negative Chebychev polynomial. Otherwise, we call a polynomial non-exceptional.
Our definition of exceptional agrees with that in [Reference Ghioca, Nguyen and YeGNY19] for polynomials. For the notion of pre-periodic varieties we refer the reader to the established literature [Reference Medvedev and ScanlonMS14, Reference Ghioca, Nguyen and YeGNY19]. Our main theorem is the following.
Theorem 1 Let ![]() $K$ be a number field and
$K$ be a number field and ![]() $\mathcal {C} \subset \mathbb {A}^{2}$ be an irreducible plane curve that is not fibral. Let
$\mathcal {C} \subset \mathbb {A}^{2}$ be an irreducible plane curve that is not fibral. Let ![]() $f \in K[X]$ of degree
$f \in K[X]$ of degree ![]() $d \geq 2$ be a non-exceptional polynomial and
$d \geq 2$ be a non-exceptional polynomial and ![]() $\alpha \in K$ be a point that is not pre-periodic under
$\alpha \in K$ be a point that is not pre-periodic under ![]() $f$. If
$f$. If
contains infinitely many points, then there exists ![]() $n \in \mathbb {Z}_{\geq 0}$ such that
$n \in \mathbb {Z}_{\geq 0}$ such that
where ![]() $\Delta \subset \mathbb {A}^{2}$ is the diagonal.
$\Delta \subset \mathbb {A}^{2}$ is the diagonal.
If ![]() $\mathcal {C}$ is fibral, then the statement is trivial and
$\mathcal {C}$ is fibral, then the statement is trivial and ![]() $\mathcal {C}$ is, up to permuting coordinates, of the form
$\mathcal {C}$ is, up to permuting coordinates, of the form ![]() $\{\gamma \}\times \mathbb {A}^{1}$ for
$\{\gamma \}\times \mathbb {A}^{1}$ for ![]() $\gamma \in \mathcal {S}_\alpha$. If
$\gamma \in \mathcal {S}_\alpha$. If ![]() $f$ is an exceptional polynomial, then Manin–Mumford for the multiplicative group (see § 2) answers most questions one might have about Zariski-closures of subsets of
$f$ is an exceptional polynomial, then Manin–Mumford for the multiplicative group (see § 2) answers most questions one might have about Zariski-closures of subsets of ![]() $\mathcal {S}_\alpha ^{2}$. If
$\mathcal {S}_\alpha ^{2}$. If ![]() $\alpha$ is pre-periodic for
$\alpha$ is pre-periodic for ![]() $f$, then
$f$, then ![]() $\mathcal {S}_\alpha$ is contained in the set of pre-periodic points of
$\mathcal {S}_\alpha$ is contained in the set of pre-periodic points of ![]() $f$ and in this case the dynamical Bogomolov conjecture for split rational maps proven by Ghioca et al. [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1] applies. We combine these theorems in a unified statement in Theorem 5. We remark that
$f$ and in this case the dynamical Bogomolov conjecture for split rational maps proven by Ghioca et al. [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1] applies. We combine these theorems in a unified statement in Theorem 5. We remark that ![]() $\Delta$ is fixed by
$\Delta$ is fixed by ![]() $(f,f)$ but not all pre-periodic curves in
$(f,f)$ but not all pre-periodic curves in ![]() $\mathbb {A}^{2}$ are pull-backs of the diagonal (see, for example, [Reference Medvedev and ScanlonMS14]).
$\mathbb {A}^{2}$ are pull-backs of the diagonal (see, for example, [Reference Medvedev and ScanlonMS14]).
Moreover an extension of Theorem 1 to either ![]() $f$ being exceptional or
$f$ being exceptional or ![]() $\alpha$ being pre-periodic fails. A whimsical explanation is that we have more structure lurking in the background if either of these conditions hold. More concretely, if
$\alpha$ being pre-periodic fails. A whimsical explanation is that we have more structure lurking in the background if either of these conditions hold. More concretely, if ![]() $f = X^{d}$ and thus exceptional, we can take any (co-prime) integers
$f = X^{d}$ and thus exceptional, we can take any (co-prime) integers ![]() $l,k$ and consider the co-set in
$l,k$ and consider the co-set in ![]() $\mathbb {G}_m^{2}$ defined by
$\mathbb {G}_m^{2}$ defined by
Then any of these co-sets contain infinitely many points in ![]() $\mathcal {S}_\alpha ^{2}$, but if we take
$\mathcal {S}_\alpha ^{2}$, but if we take ![]() $\ell,k$ to be co-prime to
$\ell,k$ to be co-prime to ![]() $d$ say, it does not define a curve as in the conclusion of the theorem. If
$d$ say, it does not define a curve as in the conclusion of the theorem. If ![]() $f$ is non-exceptional, then the only super-attracting fixed point of degree
$f$ is non-exceptional, then the only super-attracting fixed point of degree ![]() $d$ is at infinity. Thus, if
$d$ is at infinity. Thus, if ![]() $f$ is non-exceptional and
$f$ is non-exceptional and ![]() $\alpha$ is pre-periodic, say
$\alpha$ is pre-periodic, say ![]() $f^{\circ \ell }(\alpha ) = f^{\circ k}(\alpha )$ with
$f^{\circ \ell }(\alpha ) = f^{\circ k}(\alpha )$ with ![]() $\ell > k$, then the rational curve given by
$\ell > k$, then the rational curve given by ![]() $(f^{\circ \ell }(X), f^{\circ k}(X))$ provides a counterexample to a possible extension of Theorem 1. Thus, Theorem 1 is the best possible.
$(f^{\circ \ell }(X), f^{\circ k}(X))$ provides a counterexample to a possible extension of Theorem 1. Thus, Theorem 1 is the best possible.
Another way of putting Theorem 1 is to say that the only non-trivial algebraic relations that can hold between infinitely many pairs of points in ![]() $\mathcal {S}_\alpha$ are those that define
$\mathcal {S}_\alpha$ are those that define ![]() $\mathcal {S}_\alpha$ in the first place. It is straightforward to check that the reverse also holds true. Each curve that appears in the conclusion of Theorem 1 also contains infinitely many points on
$\mathcal {S}_\alpha$ in the first place. It is straightforward to check that the reverse also holds true. Each curve that appears in the conclusion of Theorem 1 also contains infinitely many points on ![]() $\mathcal {S}_\alpha ^{2}$.
$\mathcal {S}_\alpha ^{2}$.
It is not foreseeable that what is obtained in this article can be achieved with previously established methods such as applying known equidistribution results or Siegel's theorem on integral points. This is because the usual basic assumptions such as small canonical height or rationality of the points under consideration are not fulfilled in the cases we consider.
Our methods are close to transcendence techniques which introduce entirely new techniques into the study of dynamical systems. However, they also lead to a new and elementary proof of Manin–Mumford for ![]() $\mathbb {G}_m^{n}$ as was demonstrated in [Reference SchmidtSch03]. We expect there to be more applications of the methods used in this article.
$\mathbb {G}_m^{n}$ as was demonstrated in [Reference SchmidtSch03]. We expect there to be more applications of the methods used in this article.
In the assumption of Theorem 1, ![]() $\alpha$ is not pre-periodic and, thus, has positive canonical height [Reference Ghioca, Nguyen and YeGNY19]. This implies that there exists a place
$\alpha$ is not pre-periodic and, thus, has positive canonical height [Reference Ghioca, Nguyen and YeGNY19]. This implies that there exists a place ![]() $v$ of
$v$ of ![]() $K$ for which
$K$ for which ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ (where we denote by
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ (where we denote by ![]() $|\cdot |_v$ the corresponding
$|\cdot |_v$ the corresponding ![]() $v$-adic absolute value) and, consequently, for which the local canonical height of
$v$-adic absolute value) and, consequently, for which the local canonical height of ![]() $\alpha$ is positive. All points in
$\alpha$ is positive. All points in ![]() $\mathcal {S}_\alpha$ have the same local canonical height at all places of
$\mathcal {S}_\alpha$ have the same local canonical height at all places of ![]() $K$ and if there is an archimedean place at which the local height is positive, then Theorem 1 follows from Theorem 3; if there is such a non-archimedean place, then it follows from Proposition 4.1.
$K$ and if there is an archimedean place at which the local height is positive, then Theorem 1 follows from Theorem 3; if there is such a non-archimedean place, then it follows from Proposition 4.1.
In fact, in each case, we are able to show a stronger version that allows for some uniformity (see Proposition 4.1 and Theorem 10). If ![]() $v$ can be chosen to be finite and of good reduction co-prime to
$v$ can be chosen to be finite and of good reduction co-prime to ![]() $d$, we can go from small orbits to grand orbits. This is quite similar to the case of finitely generated to finite rank groups in Lang's conjecture on semi-abelian varieties that we alluded to previously.
$d$, we can go from small orbits to grand orbits. This is quite similar to the case of finitely generated to finite rank groups in Lang's conjecture on semi-abelian varieties that we alluded to previously.
We say that ![]() $v$ is a finite place of good reduction (for
$v$ is a finite place of good reduction (for ![]() $f$) if
$f$) if ![]() $f = a_0X^{d} + \sum _{i = 1}^{d}a_iX^{d-i}$ and
$f = a_0X^{d} + \sum _{i = 1}^{d}a_iX^{d-i}$ and ![]() $|a_i/a_0|_v \leq 1$ for
$|a_i/a_0|_v \leq 1$ for ![]() $i = 1, \ldots, n$. We say that
$i = 1, \ldots, n$. We say that ![]() $v$ is co-prime to
$v$ is co-prime to ![]() $d$ if
$d$ if ![]() $|d|_v = 1$.
$|d|_v = 1$.
Theorem 2 Let ![]() $K,\mathcal {C}, \Delta$ and
$K,\mathcal {C}, \Delta$ and ![]() $f$ be as in Theorem 1. Further suppose that
$f$ be as in Theorem 1. Further suppose that ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place ![]() $v$ of
$v$ of ![]() $K$ of good reduction that is co-prime to
$K$ of good reduction that is co-prime to ![]() $d$. If
$d$. If
contains infinitely many points, then there exist ![]() $n,m \in \mathbb {Z}_{\geq 0}$ such that
$n,m \in \mathbb {Z}_{\geq 0}$ such that
We may view this result as resolving the Zilber–Pink conjecture as formulated in [Reference Ghioca and NguyenGN16] for the curve ![]() $\mathcal {C} \times \{\alpha \} \subset (\mathbb {P}_1)^{3}$ and the dynamical system
$\mathcal {C} \times \{\alpha \} \subset (\mathbb {P}_1)^{3}$ and the dynamical system ![]() $(f,f,f)$.
$(f,f,f)$.
As an example of an application of Theorem 2 we can take the non-exceptional polynomial ![]() $f = X^{2} -1$ and
$f = X^{2} -1$ and ![]() $\alpha = 1/3$. Then
$\alpha = 1/3$. Then ![]() $\mathcal {G}_\alpha$ is dense in the filled Julia set of
$\mathcal {G}_\alpha$ is dense in the filled Julia set of ![]() $f$ (in
$f$ (in ![]() $\mathbb {C}$) and Theorem 2 shows that the only algebraic relations that can hold between infinitely many distinct pairs of elements in the grand orbit of
$\mathbb {C}$) and Theorem 2 shows that the only algebraic relations that can hold between infinitely many distinct pairs of elements in the grand orbit of ![]() $1/3$ are the same that define the grand orbit. We could also take the same
$1/3$ are the same that define the grand orbit. We could also take the same ![]() $f$ and
$f$ and ![]() $\alpha = 5/3$ and then
$\alpha = 5/3$ and then ![]() $\mathcal {G}_\alpha$ is dense in the complement of the Julia set and our theorem still holds. This gives a hint at the algebraic rigidity of the extended tree formed by the grand orbit under
$\mathcal {G}_\alpha$ is dense in the complement of the Julia set and our theorem still holds. This gives a hint at the algebraic rigidity of the extended tree formed by the grand orbit under ![]() $f$ at a non-pre-periodic point; at least if
$f$ at a non-pre-periodic point; at least if ![]() $f$ is non-exceptional. In contrast if
$f$ is non-exceptional. In contrast if ![]() $f = X^{d}$, then we can take the same co-set as previously (1) with
$f = X^{d}$, then we can take the same co-set as previously (1) with ![]() $k,\ell$ co-prime to
$k,\ell$ co-prime to ![]() $d$ to obtain a counterexample to an extension of Theorem 2 to exceptional polynomials. Again one could phrase the theorem as stating that the only non-trivial algebraic relations that hold between infinitely many pairs of points in
$d$ to obtain a counterexample to an extension of Theorem 2 to exceptional polynomials. Again one could phrase the theorem as stating that the only non-trivial algebraic relations that hold between infinitely many pairs of points in ![]() $\mathcal {G}_\alpha$ are those that define the set itself. In addition, in § 9 we show that Theorem 2 cannot be extended to
$\mathcal {G}_\alpha$ are those that define the set itself. In addition, in § 9 we show that Theorem 2 cannot be extended to ![]() $\alpha$ being a pre-periodic point. For the proof of Theorem 2 we also rely on work of Ghioca, Nguyen and Ye on the dynamical Bogomolov conjecture [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1]. We want to point out that we really use the Bogomolov property, not just the Manin–Mumford property in their work.
$\alpha$ being a pre-periodic point. For the proof of Theorem 2 we also rely on work of Ghioca, Nguyen and Ye on the dynamical Bogomolov conjecture [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1]. We want to point out that we really use the Bogomolov property, not just the Manin–Mumford property in their work.
Remark Using the classification theorem of Medvedev and Scanlon once, we can see that all pre-periodic curves that have non-empty intersection with ![]() $\mathcal {S}_\alpha ^{2}$ or
$\mathcal {S}_\alpha ^{2}$ or ![]() $\mathcal {G}_\alpha ^{2}$ are as in the conclusion of Theorem 1 or 2. For a proof, see Lemma 2.1.
$\mathcal {G}_\alpha ^{2}$ are as in the conclusion of Theorem 1 or 2. For a proof, see Lemma 2.1.
If there is an infinite place ![]() $v$ of
$v$ of ![]() $K$ at which
$K$ at which ![]() $f^{\circ n}(\alpha )$ tends to infinity, we deduce Theorem 1 from a new rigidity theorem (Theorem 3) that holds for non-exceptional polynomials. However, we need some notation first.
$f^{\circ n}(\alpha )$ tends to infinity, we deduce Theorem 1 from a new rigidity theorem (Theorem 3) that holds for non-exceptional polynomials. However, we need some notation first.
For any complex polynomial ![]() $f \in \mathbb {C}[X]$ of degree
$f \in \mathbb {C}[X]$ of degree ![]() $d \geq 2$, we let
$d \geq 2$, we let
where ![]() $\log ^{+}(x) = \log \max \{1, x\}$ for
$\log ^{+}(x) = \log \max \{1, x\}$ for ![]() $x \in \mathbb {R}_{\geq 0}$. This
$x \in \mathbb {R}_{\geq 0}$. This ![]() $g_f$ is the Green function attached to the Julia set of
$g_f$ is the Green function attached to the Julia set of ![]() $f$ and a continuous function on
$f$ and a continuous function on ![]() $\mathbb {C}$. For
$\mathbb {C}$. For ![]() $r > 0$, we define the equipotential curve of
$r > 0$, we define the equipotential curve of ![]() $r$ to be the level set
$r$ to be the level set
We note that for ![]() $f = X^{d}$ it holds that
$f = X^{d}$ it holds that ![]() $L_r$ is the circle of radius
$L_r$ is the circle of radius ![]() $\exp (r)$ and that for all
$\exp (r)$ and that for all ![]() $f$ the level set at 0 is the filled Julia set of
$f$ the level set at 0 is the filled Julia set of ![]() $f$. Thus,
$f$. Thus, ![]() $\alpha \in \mathbb {C}$ satisfies
$\alpha \in \mathbb {C}$ satisfies ![]() $|f^{\circ n}(\alpha )| \rightarrow \infty$ with the usual absolute value if and only if
$|f^{\circ n}(\alpha )| \rightarrow \infty$ with the usual absolute value if and only if ![]() $g_f(\alpha ) >0$.
$g_f(\alpha ) >0$.
The following is a characterisation of curves that intersect ![]() $L_r^{2}$ in infinitely many points.
$L_r^{2}$ in infinitely many points.
Theorem 3 Let ![]() $f$ be a non-exceptional polynomial with complex coefficients. If a complex connected plane curve
$f$ be a non-exceptional polynomial with complex coefficients. If a complex connected plane curve ![]() $\mathcal {C} \subset \mathbb {A}^{2}$, that is not fibral, has infinite intersection with
$\mathcal {C} \subset \mathbb {A}^{2}$, that is not fibral, has infinite intersection with ![]() $L_r^{2}$ (for some
$L_r^{2}$ (for some ![]() $r > 0$), then
$r > 0$), then ![]() $\mathcal {C}$ is a component of a curve defined by
$\mathcal {C}$ is a component of a curve defined by
for some ![]() $n \in \mathbb {Z}_{\geq 0}$ and some linear polynomial
$n \in \mathbb {Z}_{\geq 0}$ and some linear polynomial ![]() $L(X)$ such that
$L(X)$ such that ![]() $L\circ f^{\circ n} = f^{\circ n} \circ L$. Here
$L\circ f^{\circ n} = f^{\circ n} \circ L$. Here ![]() $X,Y$ are the affine coordinates on
$X,Y$ are the affine coordinates on ![]() $\mathbb {A}^{2}$.
$\mathbb {A}^{2}$.
Owing to the fact that ![]() $L_r$ is a piecewise real analytic set one can interpret Theorem 3 as a characterisation of all algebraic correspondences that preserve an equipotential curve
$L_r$ is a piecewise real analytic set one can interpret Theorem 3 as a characterisation of all algebraic correspondences that preserve an equipotential curve ![]() $L_r$. These sorts of rigidity theorems often play a key role in the proofs in arithmetic dynamics. For example, in the proof of a case of the dynamical André–Oort conjecture in [Reference Ghioca, Krieger, Nguyen and YeGKNY17, Reference Favre and GauthierFG04], a key ingredient is a classification of algebraic correspondences preserving (generalised) Mandelbrot set.
$L_r$. These sorts of rigidity theorems often play a key role in the proofs in arithmetic dynamics. For example, in the proof of a case of the dynamical André–Oort conjecture in [Reference Ghioca, Krieger, Nguyen and YeGKNY17, Reference Favre and GauthierFG04], a key ingredient is a classification of algebraic correspondences preserving (generalised) Mandelbrot set.
Theorem 3 does not hold without the requirement on ![]() $f$ to be non-exceptional. For example, taking
$f$ to be non-exceptional. For example, taking ![]() $f = X^{d}$ graphs of Möbius transformations sending
$f = X^{d}$ graphs of Möbius transformations sending ![]() $L_r$ to
$L_r$ to ![]() $L_r$ provide an ample supply of counterexamples (see, for example, the introduction of [Reference Bays and HabeggerBH15]). These counterexamples are made possible by the fact that
$L_r$ provide an ample supply of counterexamples (see, for example, the introduction of [Reference Bays and HabeggerBH15]). These counterexamples are made possible by the fact that ![]() $L_r$ is semi-algebraic. This suggests that
$L_r$ is semi-algebraic. This suggests that ![]() $L_r$ should be a transcendental curve if
$L_r$ should be a transcendental curve if ![]() $f$ is not exceptional and we can support this intuition with the following theorem whose proof is straightforward given the tools used in the proof of Theorem 3.
$f$ is not exceptional and we can support this intuition with the following theorem whose proof is straightforward given the tools used in the proof of Theorem 3.
Theorem 4 The set ![]() $L_r$ contains a connected semi-algebraic curve for some
$L_r$ contains a connected semi-algebraic curve for some ![]() $r > 0$ if and only if
$r > 0$ if and only if ![]() $f$ is exceptional.
$f$ is exceptional.
We pause to mention that we thought it is worth recording this theorem because it is analogous to Fatou's theorem [Reference FatouFat20, p. 250]: Fatou's theorem characterises exceptional polynomials as those whose Julia set is a (piecewise) analytic arc, whereas our theorem characterises exceptional polynomials through properties of ![]() $L_r$. As the curves
$L_r$. As the curves ![]() $L_r$ are always piecewise real analytic, we need a finer criterion and Theorem 3 shows that this finer criterion is (real) algebraicity. It is also worth pointing out that Fatou's theorem itself is crucial for the proof of Theorems 3 and 4.
$L_r$ are always piecewise real analytic, we need a finer criterion and Theorem 3 shows that this finer criterion is (real) algebraicity. It is also worth pointing out that Fatou's theorem itself is crucial for the proof of Theorems 3 and 4.
Another important characterisation of exceptional polynomials that we make use of is due to the combined work of Levin [Reference LevinLev91] and Douady, Hubbard and Thurston [Reference Douady and HubbardDH93]. This characterises polynomials whose Julia set has a normal family of symmetries as being exceptional. These theorems allow us to show that ‘irrational rotations’ of the basin of infinity of ![]() $f$ with connected Julia set cannot be algebraic (see Lemma 5.9).
$f$ with connected Julia set cannot be algebraic (see Lemma 5.9).
Finally, for ![]() $f$ with disconnected Julia set, we introduce considerations that seem to be entirely absent from the existing literature. Namely we study the monodromy action on Mahler functions that appear as the inverse of the famous Böttcher coordinates. This requires careful analysis of Puiseux expansions among other things. Indeed, somewhat surprisingly in the disconnected case we do not need to use any deep rigidity theorem from complex dynamics. Instead, monodromy alone seems to contain sufficient information in this case.
$f$ with disconnected Julia set, we introduce considerations that seem to be entirely absent from the existing literature. Namely we study the monodromy action on Mahler functions that appear as the inverse of the famous Böttcher coordinates. This requires careful analysis of Puiseux expansions among other things. Indeed, somewhat surprisingly in the disconnected case we do not need to use any deep rigidity theorem from complex dynamics. Instead, monodromy alone seems to contain sufficient information in this case.
As a final remark on the rigidity theorems we note that the techniques used to prove Theorems 3 and 4 potentially extend to higher dimensions to prove that for a non-exceptional polynomials the components of the intersection of an algebraic variety with powers of ![]() $L_r$ must have low dimension. This might be of interest in connection with dynamical questions and equidistribution on powers of
$L_r$ must have low dimension. This might be of interest in connection with dynamical questions and equidistribution on powers of ![]() $L_r$.
$L_r$.
At this point it seems appropriate to put Theorems 1 and 2 into the context of the dynamical literature as well. Our paper (and, in particular, Theorem 2) may be viewed as a first attempt to unify the dynamical Mordell–Lang conjecture and the dynamical Manin–Mumford conjecture.
A dynamical Mordell–Lang conjecture was first formulated by Ghioca and Tucker in [Reference Ghioca and TuckerGT09] and then further expanded on in the book [Reference Bell, Ghioca and TuckerBGT16] where the authors also discuss intersections of orbits. In [Reference Ghioca and TuckerGT09] the authors also use properties of attracting fixed points in their proof. A dynamical Manin–Mumford conjecture was first formulated by Zhang and later corrected and refined by Ghioca et al. [Reference Ghioca, Tucker and ZhangGTZ11] as well as by Ghioca and Tucker [Reference Ghioca and TuckerGT21].
On the dynamical Manin–Mumford side we mention some results that mostly concern the projective line ![]() $\mathbb {P}_1$ and its powers
$\mathbb {P}_1$ and its powers ![]() $\mathbb {P}_1^{n}$. As alluded to previously, Ghioca, Nguyen and Ye have proven the dynamical Manin–Mumford conjecture for split endomorphisms of
$\mathbb {P}_1^{n}$. As alluded to previously, Ghioca, Nguyen and Ye have proven the dynamical Manin–Mumford conjecture for split endomorphisms of ![]() $\mathbb {P}_1^{n}$. This work relied on the equidistribution theorem by Yuan on adelic heights [Reference YuanYua08]. Similarly Baker and Demarco used equidistribution techniques to prove a Manin–Mumford theorem for families of dynamical systems [Reference Baker and DeMarcoBD11]. This is by no means an exhaustive list of the results obtained by using the powerful equidistribution theorem combined with deep insights into the intricate geometry and arithmetic of dynamical systems. Worth mentioning is also the resolution of some cases of a dynamical André–Oort conjecture with these techniques [Reference Ghioca, Krieger, Nguyen and YeGKNY17].
$\mathbb {P}_1^{n}$. This work relied on the equidistribution theorem by Yuan on adelic heights [Reference YuanYua08]. Similarly Baker and Demarco used equidistribution techniques to prove a Manin–Mumford theorem for families of dynamical systems [Reference Baker and DeMarcoBD11]. This is by no means an exhaustive list of the results obtained by using the powerful equidistribution theorem combined with deep insights into the intricate geometry and arithmetic of dynamical systems. Worth mentioning is also the resolution of some cases of a dynamical André–Oort conjecture with these techniques [Reference Ghioca, Krieger, Nguyen and YeGKNY17].
On the dynamical Mordell–Lang side, the works that are perhaps closest in spirit to ours are [Reference Ghioca, Tucker and ZieveGTZ08, Reference Ghioca, Tucker and ZieveGTZ12] as they treat intersections of varieties with orbits of polynomials.
From the point of view of height theory, Theorem 1 may also be viewed as an intermediate between [Reference Ghioca, Nguyen and YeGNY19] and [Reference Ghioca, Tucker and ZieveGTZ08] as we are treating points of constant canonical height whereas the cited works treat points of small and unbounded canonical height, respectively.
In order to incorporate exceptional polynomials and periodic points in our statement we need some care to encode essentially group theoretic information in dynamical terms (see [Reference Ghioca and TuckerGT21] for related problems). What is new in our context compared with [Reference Ghioca and TuckerGT21] is that we need to define an analogue of co-sets in the dynamical setting. For this we introduce some notation. We formulate a conjecture for powers of the projective line here and in § 9 a conjecture for all projective varieties.
For an endomorphism ![]() $g$ of
$g$ of ![]() $\mathbb {P}_1$ we let
$\mathbb {P}_1$ we let ![]() $\Xi _g$ be
$\Xi _g$ be ![]() $\mathbb {P}_1\setminus \text {S}_g$ where
$\mathbb {P}_1\setminus \text {S}_g$ where ![]() $\text {S}_g$ is the set of super-attracting fixed points of
$\text {S}_g$ is the set of super-attracting fixed points of ![]() $g$ of degree
$g$ of degree ![]() $\deg (g)$ (see [Reference MilnorMil06]). The variety
$\deg (g)$ (see [Reference MilnorMil06]). The variety ![]() $\Xi _g$ is always quasi-affine. It is a natural space on which
$\Xi _g$ is always quasi-affine. It is a natural space on which ![]() $g$ acts. We say that two morphisms commute if they commute by composition.
$g$ acts. We say that two morphisms commute if they commute by composition.
Definition 2 Let ![]() $\mathcal {K}$ be an algebraically closed field of characteristic zero and
$\mathcal {K}$ be an algebraically closed field of characteristic zero and ![]() $n$ a positive integer. We say that a variety
$n$ a positive integer. We say that a variety ![]() $\mathcal {V} \subset \mathbb {P}_1^{n}$ defined over
$\mathcal {V} \subset \mathbb {P}_1^{n}$ defined over ![]() $\mathcal {K}$ is stratified by an endomorphism
$\mathcal {K}$ is stratified by an endomorphism ![]() $g$ of
$g$ of ![]() $\mathbb {P}_1$ defined over
$\mathbb {P}_1$ defined over ![]() $\mathcal {K}$ if there exists an endomorphism
$\mathcal {K}$ if there exists an endomorphism ![]() $h$ of
$h$ of ![]() $\mathbb {P}_1$ and a finite morphism
$\mathbb {P}_1$ and a finite morphism ![]() $\varphi :\Xi _h \rightarrow \Xi _g$ with the property
$\varphi :\Xi _h \rightarrow \Xi _g$ with the property ![]() $g\circ \varphi = \varphi \circ h$ such that the following holds: there exists a variety
$g\circ \varphi = \varphi \circ h$ such that the following holds: there exists a variety ![]() $\mathcal {V}_\varphi \subset \Xi _h^{n}$ and a morphism
$\mathcal {V}_\varphi \subset \Xi _h^{n}$ and a morphism ![]() $H: \Xi _h^{n} \rightarrow \Xi _h^{n}$ commuting with
$H: \Xi _h^{n} \rightarrow \Xi _h^{n}$ commuting with ![]() $(h,\ldots, h):\Xi _h^{n} \rightarrow \Xi _h^{n}$ such that
$(h,\ldots, h):\Xi _h^{n} \rightarrow \Xi _h^{n}$ such that
for some ![]() $\beta \in \Xi _g^{n-\dim (\mathcal {V})}(\mathcal {K})$.
$\beta \in \Xi _g^{n-\dim (\mathcal {V})}(\mathcal {K})$.
Definition 2 is quite technical. However, it tries to capture the fact that if a rational map comes from an algebraic group, the group structure gives rise to ‘many’ endomorphisms that commute with the given rational map in purely dynamical terms. A simple example is that ![]() $\mathcal {V}$ is stratified by
$\mathcal {V}$ is stratified by ![]() $g$ if the projection of
$g$ if the projection of ![]() $\mathcal {V}$ to a factor of
$\mathcal {V}$ to a factor of ![]() $\mathbb {P}_1$ is constant. In the exceptional cases we can think of
$\mathbb {P}_1$ is constant. In the exceptional cases we can think of ![]() $\Xi _h$ as coming from an algebraic group and
$\Xi _h$ as coming from an algebraic group and ![]() $H$ as coming from a group morphism. Note that for
$H$ as coming from a group morphism. Note that for ![]() $g= X^{2}$ any co-set of
$g= X^{2}$ any co-set of ![]() $\mathbb {G}_m^{n}$ defines a variety that is stratified by
$\mathbb {G}_m^{n}$ defines a variety that is stratified by ![]() $g$. We obtain the following from Theorem 1, [Reference Ghioca, Nguyen and YeGNY19] and Manin–Mumford.
$g$. We obtain the following from Theorem 1, [Reference Ghioca, Nguyen and YeGNY19] and Manin–Mumford.
Theorem 5 Let ![]() $f \in K[X]$ be a polynomial of degree
$f \in K[X]$ be a polynomial of degree ![]() $d \geq 2$ and let
$d \geq 2$ and let ![]() $\alpha \in K$. Let
$\alpha \in K$. Let ![]() $\mathcal {C} \subset \mathbb {A}^{2}$ be a geometrically irreducible curve over
$\mathcal {C} \subset \mathbb {A}^{2}$ be a geometrically irreducible curve over ![]() $K$. If
$K$. If ![]() $\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ contains infinitely many points, then
$\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ contains infinitely many points, then ![]() $\mathcal {C}$ is either pre-periodic under the endomorphism
$\mathcal {C}$ is either pre-periodic under the endomorphism ![]() $(f,f)$ or is stratified by
$(f,f)$ or is stratified by ![]() $f$.
$f$.
Following a suggestion of Ghioca, we formulate a conjecture for intersections of varieties with grand orbits. It can be viewed as a natural dynamical analogue of Lang's conjecture on finite rank groups.
For an endomorphism ![]() $g$ of
$g$ of ![]() $\mathbb {P}_1$ and
$\mathbb {P}_1$ and ![]() $\alpha \in \mathbb {P}_1(\mathcal {K})$ we set
$\alpha \in \mathbb {P}_1(\mathcal {K})$ we set ![]() $\mathcal {G}_\alpha (g)$ to be the grand orbit of
$\mathcal {G}_\alpha (g)$ to be the grand orbit of ![]() $\alpha$ under
$\alpha$ under ![]() $g$. Let
$g$. Let ![]() $X = \mathbb {P}_1^{n}$ and
$X = \mathbb {P}_1^{n}$ and ![]() $\underline {g} = (g_1, \ldots, g_n)$ where
$\underline {g} = (g_1, \ldots, g_n)$ where ![]() $g_1,\ldots, g_n$ are endomorphisms of
$g_1,\ldots, g_n$ are endomorphisms of ![]() $\mathbb {P}_1$ of degree at least 2 defined over
$\mathbb {P}_1$ of degree at least 2 defined over ![]() $\mathcal {K}$ as previously. Let
$\mathcal {K}$ as previously. Let ![]() $\underline {\alpha } = (\alpha _1,\ldots, \alpha _n)\in \mathbb {P}_1^{n}(\mathcal {K})$ and let
$\underline {\alpha } = (\alpha _1,\ldots, \alpha _n)\in \mathbb {P}_1^{n}(\mathcal {K})$ and let ![]() $V$ be a hypersurface in
$V$ be a hypersurface in ![]() $X$.
$X$.
Conjecture 1 Suppose that
contains infinitely many points. Then ![]() $V$ is either pre-periodic under
$V$ is either pre-periodic under ![]() $\underline {h} = (h_1,\ldots, h_n)$ where
$\underline {h} = (h_1,\ldots, h_n)$ where ![]() $h_1, \ldots, h_n$ are endomorphisms commuting with an iterate of
$h_1, \ldots, h_n$ are endomorphisms commuting with an iterate of ![]() $g_1, \ldots, g_n$, respectively, and such that at least one of
$g_1, \ldots, g_n$, respectively, and such that at least one of ![]() $h_1, \ldots, h_n$ has degree at least 2 or
$h_1, \ldots, h_n$ has degree at least 2 or ![]() $V$ is stratified by
$V$ is stratified by ![]() $g_i$ for some
$g_i$ for some ![]() $i \in \{1,\ldots, n\}$.
$i \in \{1,\ldots, n\}$.
From Theorem 2 it follows that we can treat part of Conjecture 1.
Theorem 6 Let ![]() $f \in K[X]$ and let
$f \in K[X]$ and let ![]() $\alpha \in K$ be such that
$\alpha \in K$ be such that ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place ![]() $v$ of good reduction co-prime to
$v$ of good reduction co-prime to ![]() $d$. Then Conjecture 1 holds true for
$d$. Then Conjecture 1 holds true for ![]() $\underline {\alpha } = (\alpha, \alpha )$ and
$\underline {\alpha } = (\alpha, \alpha )$ and ![]() $\underline {f} = (f,f)$.
$\underline {f} = (f,f)$.
We call a curve ![]() $\mathcal {C} \subset \mathbb {A}^{2}$ special if it is a component of curve defined by
$\mathcal {C} \subset \mathbb {A}^{2}$ special if it is a component of curve defined by ![]() $f^{\circ n}(X)- f^{\circ n}(Y) = 0$ for some
$f^{\circ n}(X)- f^{\circ n}(Y) = 0$ for some ![]() $n \geq 0$ or if
$n \geq 0$ or if ![]() $\mathcal {C}$ is of the form
$\mathcal {C}$ is of the form ![]() $\{\beta \} \times \mathbb {A}^{1}$ or
$\{\beta \} \times \mathbb {A}^{1}$ or ![]() $\mathbb {A}^{1}\times \{\beta \}$ for some
$\mathbb {A}^{1}\times \{\beta \}$ for some ![]() $\beta \in \mathcal {S}_\alpha$.
$\beta \in \mathcal {S}_\alpha$.
It is also possible to put Theorem 1 in the more classical context of unlikely intersections. More precisely, we define the set of special subvarieties ![]() $\text {Sp}_f$ of
$\text {Sp}_f$ of ![]() $\mathbb {A}^{3}$ with coordinates
$\mathbb {A}^{3}$ with coordinates ![]() $(X_1,X_2,X_3)$ to be Boolean combinations of varieties defined by
$(X_1,X_2,X_3)$ to be Boolean combinations of varieties defined by
Theorem 1 implies that for ![]() $\alpha$ that is not pre-periodic under
$\alpha$ that is not pre-periodic under ![]() $f$ and
$f$ and ![]() $f$ non-exceptional, the intersection
$f$ non-exceptional, the intersection
 \begin{align*} \mathcal{C} \times \{\alpha\} \cap\bigg(\bigcup_{V \in \text{Sp}_f, \text{codim}(V) > 1} V\bigg) \end{align*}
\begin{align*} \mathcal{C} \times \{\alpha\} \cap\bigg(\bigcup_{V \in \text{Sp}_f, \text{codim}(V) > 1} V\bigg) \end{align*}
is finite unless ![]() $\mathcal {C}\times \{\alpha \}$ is contained in a special subvariety of positive codimension.
$\mathcal {C}\times \{\alpha \}$ is contained in a special subvariety of positive codimension.
It is useful to keep this terminology and we often refer to a special curve in ![]() $\mathbb {A}^{2}$ to be either of the form
$\mathbb {A}^{2}$ to be either of the form ![]() $\{\beta \}\times \mathbb {A}^{1}$ or
$\{\beta \}\times \mathbb {A}^{1}$ or ![]() $\mathbb {A}^{1}\times \{\beta \}$ for some
$\mathbb {A}^{1}\times \{\beta \}$ for some ![]() $\beta \in \mathcal {S}_\alpha$ or if
$\beta \in \mathcal {S}_\alpha$ or if ![]() $\mathcal {C}$ is a component of the variety defined by
$\mathcal {C}$ is a component of the variety defined by ![]() $f^{\circ n}(X) = f^{\circ n}(Y)$, respectively.
$f^{\circ n}(X) = f^{\circ n}(Y)$, respectively.
We now summarise the discussion of our methods and compare them with the Pila–Zannier method which is often used in special circumstances. As mentioned previously, we localise at a place ![]() $v$ for which
$v$ for which ![]() $\alpha$ lies in its associated basin of infinity. If the place turns out to be archimedean we reduce Theorem 1 to a rigidity theorem (Theorem 3) that is really an analytic property of the dynamical system. If
$\alpha$ lies in its associated basin of infinity. If the place turns out to be archimedean we reduce Theorem 1 to a rigidity theorem (Theorem 3) that is really an analytic property of the dynamical system. If ![]() $v$ is non-archimedean, however, we make use of the ‘uniformisation’ of the dynamical system by the inverse of the Böttcher map. Quite similarly as in the Pila–Zannier method, we study the pullback of the curve
$v$ is non-archimedean, however, we make use of the ‘uniformisation’ of the dynamical system by the inverse of the Böttcher map. Quite similarly as in the Pila–Zannier method, we study the pullback of the curve ![]() $\mathcal {C}$ by this uniformisation and show a functional transcendence result for this pull-back. However, we only show that the pull-back is not contained in a co-set of
$\mathcal {C}$ by this uniformisation and show a functional transcendence result for this pull-back. However, we only show that the pull-back is not contained in a co-set of ![]() $\mathbb {G}_m^{2}$ unless
$\mathbb {G}_m^{2}$ unless ![]() $\mathcal {C}$ is special (Theorems 7 and 8). We essentially study pairs of roots of unity on our pull-back and these are of bounded height but not of bounded degree. This rules out the possibility to directly apply counting of rational points in the Pila–Wilkie style.
$\mathcal {C}$ is special (Theorems 7 and 8). We essentially study pairs of roots of unity on our pull-back and these are of bounded height but not of bounded degree. This rules out the possibility to directly apply counting of rational points in the Pila–Wilkie style.
Our approach is different and seems to be particularly suited for non-archimedean completions. To a fixed solution ![]() $(\beta _1,\beta _2) \in \mathcal {S}_\alpha ^{2}\cap \mathcal {C}$ we construct an auxiliary function that vanishes at the pull-back of the whole Galois orbit of
$(\beta _1,\beta _2) \in \mathcal {S}_\alpha ^{2}\cap \mathcal {C}$ we construct an auxiliary function that vanishes at the pull-back of the whole Galois orbit of ![]() $(\beta _1,\beta _2)$. We then apply Poisson–Jensen to bound its zero set, which does not care about the degree of the point. Our method is suited for generalisations and we explore it further in the function field case in future work. As we showed in [Reference SchmidtSch03], and have already mentioned, it leads to a new and quite elementary proof of (the classical) Manin–Mumford in the multiplicative group.
$(\beta _1,\beta _2)$. We then apply Poisson–Jensen to bound its zero set, which does not care about the degree of the point. Our method is suited for generalisations and we explore it further in the function field case in future work. As we showed in [Reference SchmidtSch03], and have already mentioned, it leads to a new and quite elementary proof of (the classical) Manin–Mumford in the multiplicative group.
As we often work with roots of unity, we set ![]() $\mu _{\infty }$ to be the set of all roots of 1 and
$\mu _{\infty }$ to be the set of all roots of 1 and ![]() $\mu _{d^{\infty }}$ the set of roots of unity whose order divides a power of
$\mu _{d^{\infty }}$ the set of roots of unity whose order divides a power of ![]() $d$. Finally, for a positive integer
$d$. Finally, for a positive integer ![]() $N$ we set
$N$ we set ![]() $\mu _N$ to be the set of the
$\mu _N$ to be the set of the ![]() $N$th root of 1. For a field
$N$th root of 1. For a field ![]() $\mathcal {K}$ (often
$\mathcal {K}$ (often ![]() $K$) we set
$K$) we set ![]() $\mathcal {K}_v$ to be its completion by the valuation
$\mathcal {K}_v$ to be its completion by the valuation ![]() $v$ and set
$v$ and set ![]() $\bar {\mathcal {K}}$ to be its algebraic closure. We denote by
$\bar {\mathcal {K}}$ to be its algebraic closure. We denote by ![]() $h,H:\bar {\mathbb {Q}} \rightarrow \mathbb {R}$ the logarithmic, multiplicative, respectively, (naive) Weil height [Reference Bombieri and GublerBG06].
$h,H:\bar {\mathbb {Q}} \rightarrow \mathbb {R}$ the logarithmic, multiplicative, respectively, (naive) Weil height [Reference Bombieri and GublerBG06].
Here is how we proceed. In the next section, we reduce the last two theorems in this section to Theorems 1 and 2. Then we introduce the main players in our proof which are the Mahler functions defined by ![]() $f$. In § 4 we give the proof of a uniform version of Theorem 1 when
$f$. In § 4 we give the proof of a uniform version of Theorem 1 when ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place. In § 5 we give the proof of Theorem 3 when the Julia set of
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place. In § 5 we give the proof of Theorem 3 when the Julia set of ![]() $f$ is connected and in § 6 when it is disconnected. We summarise the proof of Theorem 1 in § 7 and in § 8 we give the proof of Theorem 2. We conclude in the final section with some remarks and give a uniform version of Theorem 3.
$f$ is connected and in § 6 when it is disconnected. We summarise the proof of Theorem 1 in § 7 and in § 8 we give the proof of Theorem 2. We conclude in the final section with some remarks and give a uniform version of Theorem 3.
2. Reductions
We first note that if Theorem 1 holds for a polynomial ![]() $f$, then it holds for
$f$, then it holds for ![]() $L\circ f\circ L^{-1}$ for any linear polynomial
$L\circ f\circ L^{-1}$ for any linear polynomial ![]() $L$. The same holds for Theorem 3. Thus, we may and do assume that
$L$. The same holds for Theorem 3. Thus, we may and do assume that ![]() $f$ is monic.
$f$ is monic.
We now reduce Theorem 5 to Theorem 1. If ![]() $\alpha$ is pre-periodic under
$\alpha$ is pre-periodic under ![]() $f$, then Theorem 5 follows from Theorem 1.1 in [Reference Ghioca, Nguyen and YeGNY19] and this case is taken care of. Now assume that
$f$, then Theorem 5 follows from Theorem 1.1 in [Reference Ghioca, Nguyen and YeGNY19] and this case is taken care of. Now assume that ![]() $f$ is exceptional. Then we may assume that
$f$ is exceptional. Then we may assume that ![]() $f$ is either Chebychev or a power map. In both cases there exists a morphism
$f$ is either Chebychev or a power map. In both cases there exists a morphism ![]() $\varphi : \mathbb {G}_m \rightarrow \Xi _f$ such that
$\varphi : \mathbb {G}_m \rightarrow \Xi _f$ such that ![]() $f\circ \varphi (X) = \varphi (X^{d})$. In the former cases
$f\circ \varphi (X) = \varphi (X^{d})$. In the former cases ![]() $\varphi (X) = X + 1/X$ and in the latter it is
$\varphi (X) = X + 1/X$ and in the latter it is ![]() $\varphi (X) = X$. It follows that for each
$\varphi (X) = X$. It follows that for each ![]() $(\beta _1, \beta _2) \in \mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ there exists a pair of roots of unity
$(\beta _1, \beta _2) \in \mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ there exists a pair of roots of unity ![]() $(\zeta _1, \zeta _2)$ such that
$(\zeta _1, \zeta _2)$ such that ![]() $(\varphi (\alpha \zeta _1), \varphi (\alpha \zeta _2)) = (\beta _1, \beta _2)$. Thus, if there exist infinitely many points in
$(\varphi (\alpha \zeta _1), \varphi (\alpha \zeta _2)) = (\beta _1, \beta _2)$. Thus, if there exist infinitely many points in ![]() $\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ then one of the components of
$\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ then one of the components of ![]() $(\varphi, \varphi )^{-1}(\mathcal {C})$ is equal to a co-set (by Manin–Mumford). Calling this co-set
$(\varphi, \varphi )^{-1}(\mathcal {C})$ is equal to a co-set (by Manin–Mumford). Calling this co-set ![]() $\mathcal {C}_\varphi$ and letting
$\mathcal {C}_\varphi$ and letting ![]() $H$ be a coordinate-wise monomial sending
$H$ be a coordinate-wise monomial sending ![]() $\mathcal {C}_\varphi$ to
$\mathcal {C}_\varphi$ to ![]() $\{\beta \}\times \mathbb {G}_m$ for some
$\{\beta \}\times \mathbb {G}_m$ for some ![]() $\beta \in \bar {\mathbb {Q}}$ we obtain that
$\beta \in \bar {\mathbb {Q}}$ we obtain that ![]() $\mathcal {C}$ is stratified by
$\mathcal {C}$ is stratified by ![]() $f$. Thus, we have shown that Theorem 5 is a consequence of [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1], Manin–Mumford for
$f$. Thus, we have shown that Theorem 5 is a consequence of [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.1], Manin–Mumford for ![]() $\mathbb {G}_m^{2}$ and Theorem 1.
$\mathbb {G}_m^{2}$ and Theorem 1.
For the reduction of Theorem 6 to Theorem 2 we can imitate the proof given previously. However, instead of Manin–Mumford we employ the results in [Reference LaurentLau84].
Now we prove a lemma that classifies pre-periodic curves that have non-empty intersection with the grand or small orbit of a point ![]() $(\alpha,\alpha )$.
$(\alpha,\alpha )$.
Lemma 2.1 Let ![]() $\mathcal {C}, K, \alpha, \Delta$ be as in Theorem 1. If
$\mathcal {C}, K, \alpha, \Delta$ be as in Theorem 1. If ![]() $\mathcal {C}$ is pre-periodic by
$\mathcal {C}$ is pre-periodic by ![]() $(f,f)$ and
$(f,f)$ and ![]() $\mathcal {C} \cap \mathcal {G}_\alpha ^{2}$ is non-empty, then there exist
$\mathcal {C} \cap \mathcal {G}_\alpha ^{2}$ is non-empty, then there exist ![]() $n,m \in \mathbb {Z}_{\geq 0}$ such that
$n,m \in \mathbb {Z}_{\geq 0}$ such that
Moreover, if ![]() $\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ is non-empty, then
$\mathcal {C} \cap \mathcal {S}_\alpha ^{2}$ is non-empty, then ![]() $n = m$. That is, there exists
$n = m$. That is, there exists ![]() $n \in \mathbb {Z}_{\geq 0}$ such that
$n \in \mathbb {Z}_{\geq 0}$ such that
Proof. We first replace ![]() $\mathcal {C}$ by an iterate of
$\mathcal {C}$ by an iterate of ![]() $\mathcal {C}, (f^{\circ N},f^{\circ N})(\mathcal {C})$ that is periodic by
$\mathcal {C}, (f^{\circ N},f^{\circ N})(\mathcal {C})$ that is periodic by ![]() $(f,f)$. By the classification of periodic subvarieties [Reference Medvedev and ScanlonMS14, Theorem 6.2.4], there exists a polynomial
$(f,f)$. By the classification of periodic subvarieties [Reference Medvedev and ScanlonMS14, Theorem 6.2.4], there exists a polynomial ![]() $g$, commuting with some iterate
$g$, commuting with some iterate ![]() $f^{\circ M}$ of
$f^{\circ M}$ of ![]() $f$ such that after possibly permuting
$f$ such that after possibly permuting ![]() $X,Y$ our curve
$X,Y$ our curve ![]() $\mathcal {C}$ is the zero-locus of
$\mathcal {C}$ is the zero-locus of
Now take ![]() $(\beta, g(\beta )) \in \mathcal {G}_\alpha ^{2}$. There exist
$(\beta, g(\beta )) \in \mathcal {G}_\alpha ^{2}$. There exist ![]() $\ell, k \geq 0$ such that
$\ell, k \geq 0$ such that
However, then it holds for all ![]() $i \in \mathbb {Z}_{\geq 0}$, such that
$i \in \mathbb {Z}_{\geq 0}$, such that ![]() $k + i \in \mathbb {Z}_{\geq 0}M$, that
$k + i \in \mathbb {Z}_{\geq 0}M$, that
If ![]() $k \geq \ell$, then we deduce that
$k \geq \ell$, then we deduce that ![]() $g \circ f^{\circ k - \ell }$ fixes
$g \circ f^{\circ k - \ell }$ fixes ![]() $f^{\circ \ell + i}(\beta )$ for infinitely many
$f^{\circ \ell + i}(\beta )$ for infinitely many ![]() $i$. As
$i$. As ![]() $\beta$ is not pre-periodic by
$\beta$ is not pre-periodic by ![]() $f$, we infer that
$f$, we infer that ![]() $g \circ f^{\circ k - \ell }$ is the identity which implies that
$g \circ f^{\circ k - \ell }$ is the identity which implies that ![]() $k = \ell$ and
$k = \ell$ and ![]() $g = \text {Id}$. Thus, we have proven the lemma if such
$g = \text {Id}$. Thus, we have proven the lemma if such ![]() $\beta$ exist and, in particular, if
$\beta$ exist and, in particular, if ![]() $\mathcal {C} \cap \mathcal {S}_\alpha$ is non-empty. If
$\mathcal {C} \cap \mathcal {S}_\alpha$ is non-empty. If ![]() $k < \ell$, then
$k < \ell$, then
for infinitely many ![]() $i \in \mathbb {Z}_{\geq 0}$ and thus
$i \in \mathbb {Z}_{\geq 0}$ and thus ![]() $g = f^{\circ \ell -k}$, which finishes the proof.
$g = f^{\circ \ell -k}$, which finishes the proof.
3. Mahler functions and Böttcher coordinates
For any field ![]() $\mathcal {K}$ (of characteristic zero) and any monic polynomial
$\mathcal {K}$ (of characteristic zero) and any monic polynomial ![]() $f \in \mathcal {K}[X]$ of degree
$f \in \mathcal {K}[X]$ of degree ![]() $d \geq 2$ there exists a unique Laurent series
$d \geq 2$ there exists a unique Laurent series ![]() $\Psi \in ( 1/X)\mathcal {K}[[X]]$ that satisfies
$\Psi \in ( 1/X)\mathcal {K}[[X]]$ that satisfies
and has a pole of residue 1 at 0 [Reference IngramIng13]. For example, for ![]() $f = X^{d}$, we have
$f = X^{d}$, we have ![]() $\Psi (X) = 1/X$. Equation (3) defines a Mahler function [Reference NishiokaNis96] which is a well-studied class of functions in transcendental number theory. If
$\Psi (X) = 1/X$. Equation (3) defines a Mahler function [Reference NishiokaNis96] which is a well-studied class of functions in transcendental number theory. If ![]() $\mathcal {K}$ is a valued field with value
$\mathcal {K}$ is a valued field with value ![]() $v$, there exists a maximal
$v$, there exists a maximal ![]() $R^{v} \in \mathbb {R}_{> 0}\cup \{\infty \}$ such that
$R^{v} \in \mathbb {R}_{> 0}\cup \{\infty \}$ such that ![]() $\Psi$ defines a meromorphic function on
$\Psi$ defines a meromorphic function on
and, moreover, there exists an inverse ![]() $\Phi \in ({1}/{X})\mathcal {K}[[1/X]]$ on
$\Phi \in ({1}/{X})\mathcal {K}[[1/X]]$ on ![]() $\Psi (D_{v}^{*})$ (where
$\Psi (D_{v}^{*})$ (where ![]() $D_{v}^{*} = D_v\setminus \{0\}$) that then satisfies
$D_{v}^{*} = D_v\setminus \{0\}$) that then satisfies
For non-archimedean places this was (to the best of the author's knowledge) introduced by Ingram in [Reference IngramIng13] and then further developed in [Reference DeMarco, Ghioca, Krieger, Nguyen, Tucker and YeDGK+19]. This inverse ![]() $\Phi$ is called the Böttcher coordinate associated to
$\Phi$ is called the Böttcher coordinate associated to ![]() $f$. Our proofs crucially rely on properties of these functions that allow the action of
$f$. Our proofs crucially rely on properties of these functions that allow the action of ![]() $f$ to be conjugated to the more well-understood action of the power map. Another viewpoint is that they provide the analogue of a Tate parametrisation.
$f$ to be conjugated to the more well-understood action of the power map. Another viewpoint is that they provide the analogue of a Tate parametrisation.
Now we return to a polynomial ![]() $f \in K[X]$ for a number field
$f \in K[X]$ for a number field ![]() $K$. Our first remark is that at almost all places
$K$. Our first remark is that at almost all places ![]() $v$ of
$v$ of ![]() $K$ it holds that
$K$ it holds that ![]() $R^{v} = 1$ (see [Reference DeMarco, Ghioca, Krieger, Nguyen, Tucker and YeDGK+19, Theorem 6.5]) and that for non-exceptional polynomials
$R^{v} = 1$ (see [Reference DeMarco, Ghioca, Krieger, Nguyen, Tucker and YeDGK+19, Theorem 6.5]) and that for non-exceptional polynomials ![]() $R^{v} \leq 1$ at all places
$R^{v} \leq 1$ at all places ![]() $v$.
$v$.
For ![]() $\alpha \in K$, it holds that either
$\alpha \in K$, it holds that either ![]() $\alpha$ is a pre-periodic point of
$\alpha$ is a pre-periodic point of ![]() $f$ or there exists a place
$f$ or there exists a place ![]() $v$ of
$v$ of ![]() $K$ such that
$K$ such that ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ (see [Reference Boxall, Jones and SchmidtBJS22, Proof of Theorem 6.1]). In particular, for each
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ (see [Reference Boxall, Jones and SchmidtBJS22, Proof of Theorem 6.1]). In particular, for each ![]() $\alpha$ that is not pre-periodic there exists
$\alpha$ that is not pre-periodic there exists ![]() $N$ such that
$N$ such that ![]() $f^{\circ N}(\alpha ) \in \Psi (D_{v}^{*})$ at some place
$f^{\circ N}(\alpha ) \in \Psi (D_{v}^{*})$ at some place ![]() $v$. Theorem 1 is invariant under replacing
$v$. Theorem 1 is invariant under replacing ![]() $\alpha$ by an iterate
$\alpha$ by an iterate ![]() $f^{\circ N}(\alpha )$. If we can find a curve
$f^{\circ N}(\alpha )$. If we can find a curve ![]() $\mathcal {C}$ that intersects
$\mathcal {C}$ that intersects ![]() $\mathcal {S}_\alpha ^{2}$ in infinitely many points, then
$\mathcal {S}_\alpha ^{2}$ in infinitely many points, then ![]() $(f^{\circ N},f^{\circ N})(\mathcal {C})$ will intersect
$(f^{\circ N},f^{\circ N})(\mathcal {C})$ will intersect ![]() $\mathcal {S}_{f^{\circ N}(\alpha )}^{2}$ in infinitely many points. And if
$\mathcal {S}_{f^{\circ N}(\alpha )}^{2}$ in infinitely many points. And if ![]() $(f^{\circ N},f^{\circ N})(\mathcal {C})$ is special, then
$(f^{\circ N},f^{\circ N})(\mathcal {C})$ is special, then ![]() $\mathcal {C}$ is as well. Thus, we may work in
$\mathcal {C}$ is as well. Thus, we may work in ![]() $\Psi (D_{v}^{*})$ and choose
$\Psi (D_{v}^{*})$ and choose ![]() $\alpha$ such that
$\alpha$ such that
Now enters another dichotomy. We either have that the place ![]() $v$ we chose is finite or infinite. Our proof follows a divide-and-conquer strategy and in the next section we are going to treat the finite places.
$v$ we chose is finite or infinite. Our proof follows a divide-and-conquer strategy and in the next section we are going to treat the finite places.
4. Non-archimedean places
In this section we assume that ![]() $f \in K[X]$ for a number field
$f \in K[X]$ for a number field ![]() $K$ (
$K$ (![]() $\alpha \in K$) and that
$\alpha \in K$) and that ![]() $f$ is monic and non-exceptional. Assume that
$f$ is monic and non-exceptional. Assume that ![]() $\alpha \in \Psi (D_{v}^{*})$ for a finite place
$\alpha \in \Psi (D_{v}^{*})$ for a finite place ![]() $v$ of
$v$ of ![]() $K$ and that (5) holds. We set
$K$ and that (5) holds. We set
and we are going to prove the following uniform version of Theorem 1 for ![]() $\alpha$ whose orbit tends to infinity at a finite place. We need the uniformity in the orbit of
$\alpha$ whose orbit tends to infinity at a finite place. We need the uniformity in the orbit of ![]() $\alpha$ to prove Theorem 2.
$\alpha$ to prove Theorem 2.
Proposition 4.1 Suppose there is a finite place ![]() $v$ of
$v$ of ![]() $K$ for which
$K$ for which ![]() $\alpha \in \Psi (D_{v}^{*})$. Let
$\alpha \in \Psi (D_{v}^{*})$. Let ![]() $\mathcal {C}$ be an irreducible plane curve and suppose that
$\mathcal {C}$ be an irreducible plane curve and suppose that ![]() $\mathcal {C}$ is not special. Then there exists a constant
$\mathcal {C}$ is not special. Then there exists a constant ![]() $C = C(\alpha, \mathcal {C})$ such that if
$C = C(\alpha, \mathcal {C})$ such that if ![]() $(\beta _1, \beta _2) \in \mathcal {C}(\bar {\mathbb {Q}}) \cap \mathcal {S}_{\beta }^{2}$ for some
$(\beta _1, \beta _2) \in \mathcal {C}(\bar {\mathbb {Q}}) \cap \mathcal {S}_{\beta }^{2}$ for some ![]() $\beta \in \mathcal {O}_\alpha$, then
$\beta \in \mathcal {O}_\alpha$, then ![]() $f^{\circ n}(\alpha ) = f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2)$ for some
$f^{\circ n}(\alpha ) = f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2)$ for some ![]() $n \leq C$.
$n \leq C$.
This proposition directly implies Theorem 1 if ![]() $|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place
$|f^{\circ n}(\alpha )|_v \rightarrow \infty$ at a finite place ![]() $v$ of
$v$ of ![]() $K$.
$K$.
In what follows in this section, we set ![]() $D = D_v$ where
$D = D_v$ where ![]() $D_v$ is, as in the previous section, the maximal disc on which
$D_v$ is, as in the previous section, the maximal disc on which ![]() $\Psi$ is meromorphic and, similarly,
$\Psi$ is meromorphic and, similarly,
For non-archimedean places the absolute value behaves strikingly simply. It holds that ![]() $|\Psi (z)|_v = |z|_v^{-1}$ and that
$|\Psi (z)|_v = |z|_v^{-1}$ and that ![]() $\Psi$ is a bi-holomorphism
$\Psi$ is a bi-holomorphism
with inverse ![]() $\Phi$.
$\Phi$.
We first give a brief informal description of the proof of Proposition 4.1. We consider the polynomial ![]() $P$ whose zero-locus defines
$P$ whose zero-locus defines ![]() $\mathcal {C}$ and fix a point
$\mathcal {C}$ and fix a point ![]() $(\beta _1, \beta _2) \in \mathcal {C} \cap \mathcal {S}_\alpha ^{2}$. Due to our conditions on
$(\beta _1, \beta _2) \in \mathcal {C} \cap \mathcal {S}_\alpha ^{2}$. Due to our conditions on ![]() $\alpha$ we conclude that
$\alpha$ we conclude that
where ![]() $\zeta _1, \zeta _2$ are roots of unity. The goal now is to bound the order
$\zeta _1, \zeta _2$ are roots of unity. The goal now is to bound the order ![]() $N$ of
$N$ of ![]() $(\zeta _1, \zeta _2) \in \mathbb {G}_m^{2}$, which will lead to the bound on
$(\zeta _1, \zeta _2) \in \mathbb {G}_m^{2}$, which will lead to the bound on ![]() $n$ in Proposition 4.1. In order to achieve this we first rewrite
$n$ in Proposition 4.1. In order to achieve this we first rewrite ![]() $(\zeta _1, \zeta _2)$ as
$(\zeta _1, \zeta _2)$ as
where ![]() $\zeta _1', \zeta _2'$ are auxiliary roots of unity of small order (see Lemma 4.5) and
$\zeta _1', \zeta _2'$ are auxiliary roots of unity of small order (see Lemma 4.5) and ![]() $k_1, k_2$ are also small compared with
$k_1, k_2$ are also small compared with ![]() $N$. With the help of this re-parametrisation of the roots of unity, we can construct an auxiliary function
$N$. With the help of this re-parametrisation of the roots of unity, we can construct an auxiliary function
which is a non-archimedean analytic function on an open annulus that has the property that
We then bound the number of zeros of ![]() $a$ with the help of Lemma 4.6 and compare this bound with a lower bound for the Galois orbit of
$a$ with the help of Lemma 4.6 and compare this bound with a lower bound for the Galois orbit of ![]() $\zeta _N$ over
$\zeta _N$ over ![]() $K_v$ (Lemma 4.7). The main bulk of the argument is concerned with bounding the number of zeros of
$K_v$ (Lemma 4.7). The main bulk of the argument is concerned with bounding the number of zeros of ![]() $a$. However, the first crucial step is to show that
$a$. However, the first crucial step is to show that ![]() $a(x)$ is not the zero function. This is where a result from transcendence theory comes in. We rely on work on Mahler functions by Nishioka and Ritt as well as its non-archimedean generalisations by Corvaja and Zannier (see Theorem 8). Their work shows that if
$a(x)$ is not the zero function. This is where a result from transcendence theory comes in. We rely on work on Mahler functions by Nishioka and Ritt as well as its non-archimedean generalisations by Corvaja and Zannier (see Theorem 8). Their work shows that if ![]() $\alpha$ is an algebraic number,
$\alpha$ is an algebraic number, ![]() $\Phi (\alpha )$ is transcendental over
$\Phi (\alpha )$ is transcendental over ![]() $\bar {\mathbb {Q}}$. In combination with our Theorem 7 this indeed shows that
$\bar {\mathbb {Q}}$. In combination with our Theorem 7 this indeed shows that ![]() $a$ is not the zero function unless
$a$ is not the zero function unless ![]() $\mathcal {C}$ is a pull-back of the diagonal by an iterate of
$\mathcal {C}$ is a pull-back of the diagonal by an iterate of ![]() $(f,f)$.
$(f,f)$.
In order to work with non-archimedean analytic functions, we need the notion of annuli and use the notation
for an interval ![]() $I \subset \mathbb {R}$. Moreover, we denote by
$I \subset \mathbb {R}$. Moreover, we denote by
 \begin{align*} \mathcal{A}I= \bigg\{ \sum_{n \in \mathbb{Z}}a_n z^{n}; a_n \in \bar{K}_v, \lim_{|n| \rightarrow \infty}|a_n|_vr^{n} = 0 \text{ for all } r \in I \bigg\} \end{align*}
\begin{align*} \mathcal{A}I= \bigg\{ \sum_{n \in \mathbb{Z}}a_n z^{n}; a_n \in \bar{K}_v, \lim_{|n| \rightarrow \infty}|a_n|_vr^{n} = 0 \text{ for all } r \in I \bigg\} \end{align*}
the ring of analytic functions on ![]() $AI$. For a concise treatment of this see [Reference CherryChe09].
$AI$. For a concise treatment of this see [Reference CherryChe09].
4.1 Functional transcendence
In this subsection, let ![]() $P\in K[X,Y]\setminus \{0\}$ be an absolutely irreducible polynomial. We are going to prove a functional transcendence statement that is crucial for the proof of Proposition 4.1. For the next theorem we do not need to assume that
$P\in K[X,Y]\setminus \{0\}$ be an absolutely irreducible polynomial. We are going to prove a functional transcendence statement that is crucial for the proof of Proposition 4.1. For the next theorem we do not need to assume that ![]() $f$ is non-exceptional and it is easy to see that the theorem holds for exceptional polynomials.
$f$ is non-exceptional and it is easy to see that the theorem holds for exceptional polynomials.
It basically states that the image of certain co-sets in ![]() $\mathbb {G}_m^{2}$ by
$\mathbb {G}_m^{2}$ by ![]() $(\Psi, \Psi )$ are transcendental sets unless the image of the co-set is contained in a special curve.
$(\Psi, \Psi )$ are transcendental sets unless the image of the co-set is contained in a special curve.
Theorem 7 Let ![]() $(k_1,k_2) \in \mathbb {Z}^{2} \setminus \{(0,0)\}, \zeta _1, \zeta _2 \in \mu _{\infty }$ and let
$(k_1,k_2) \in \mathbb {Z}^{2} \setminus \{(0,0)\}, \zeta _1, \zeta _2 \in \mu _{\infty }$ and let ![]() $a \in D^{*}$ be transcendental such that
$a \in D^{*}$ be transcendental such that ![]() $a^{1/d} \in D^{*}$. Then
$a^{1/d} \in D^{*}$. Then
defines an element of ![]() $\mathcal {A}I$, where
$\mathcal {A}I$, where ![]() $I$ is an open interval defined by the conditions
$I$ is an open interval defined by the conditions
If
defines the zero function in ![]() $x$, then
$x$, then ![]() $k_1k_2(k_1-k_2) = 0$.
$k_1k_2(k_1-k_2) = 0$.
Proof. After possibly replacing ![]() $x$ by
$x$ by ![]() $1/x$ and relabelling variables, we may assume that
$1/x$ and relabelling variables, we may assume that ![]() $k_1 \geq 0$ and
$k_1 \geq 0$ and ![]() $|k_1| \geq |k_2|$. We may also replace
$|k_1| \geq |k_2|$. We may also replace ![]() $a$ by
$a$ by ![]() $\zeta _1 a$ and set
$\zeta _1 a$ and set ![]() $\zeta = \zeta _2\zeta _1^{-1}$. We pass to the polynomial
$\zeta = \zeta _2\zeta _1^{-1}$. We pass to the polynomial ![]() $P^{*} = X^{\deg _XP}Y^{\deg _YP}P(1/X,1/Y)$ and note that the theorem is equivalent to showing that if
$P^{*} = X^{\deg _XP}Y^{\deg _YP}P(1/X,1/Y)$ and note that the theorem is equivalent to showing that if ![]() $P^{*}(\Psi (ax^{k_1}),\Psi (\zeta ax^{k_2})) = 0$ identically, then
$P^{*}(\Psi (ax^{k_1}),\Psi (\zeta ax^{k_2})) = 0$ identically, then ![]() $(k_1-k_2)k_1k_2 = 0$. We set
$(k_1-k_2)k_1k_2 = 0$. We set ![]() $\mathcal {N}^{*}(x,y) = P^{*}(\Psi (x), \Psi (y))$ and will work with the expansion of
$\mathcal {N}^{*}(x,y) = P^{*}(\Psi (x), \Psi (y))$ and will work with the expansion of ![]() $\mathcal {N}^{*}$
$\mathcal {N}^{*}$
and note that ![]() $\mathcal {N}^{*}$ is an analytic function on
$\mathcal {N}^{*}$ is an analytic function on ![]() $(D^{*})^{2}$. Here
$(D^{*})^{2}$. Here ![]() $p$ is a fixed integer depending on
$p$ is a fixed integer depending on ![]() $\mathcal {C}$. If
$\mathcal {C}$. If ![]() $k_1k_2 > 0$ we consider the series expansion of
$k_1k_2 > 0$ we consider the series expansion of ![]() $\nu ^{*} = P^{*}(\Psi (ax^{k_1}), \Psi (\zeta ax^{k_2}))$
$\nu ^{*} = P^{*}(\Psi (ax^{k_1}), \Psi (\zeta ax^{k_2}))$
and if ![]() $k_1 -k_2 \neq 0$, then, for each
$k_1 -k_2 \neq 0$, then, for each ![]() $\ell \in \mathbb {Z}$, there is at most one solution
$\ell \in \mathbb {Z}$, there is at most one solution ![]() $(n,m) \in \mathbb {Z}_{\geq p}^{2}$ to
$(n,m) \in \mathbb {Z}_{\geq p}^{2}$ to ![]() $k_1n + k_2m = k, n + m = \ell$. Moreover, as
$k_1n + k_2m = k, n + m = \ell$. Moreover, as ![]() $k_1, k_2,n,m \in \mathbb {Z}_{\geq p}, c_k$ is a polynomial in
$k_1, k_2,n,m \in \mathbb {Z}_{\geq p}, c_k$ is a polynomial in ![]() $a$ with coefficients in
$a$ with coefficients in ![]() $\bar {\mathbb {Q}}$. Thus, if
$\bar {\mathbb {Q}}$. Thus, if ![]() $\nu ^{*} = 0$ identically, then as
$\nu ^{*} = 0$ identically, then as ![]() $a$ is transcendental
$a$ is transcendental ![]() $c_{nm} = 0$ for all
$c_{nm} = 0$ for all ![]() $n,m \in \mathbb {Z}_{\geq p}$ which contradicts
$n,m \in \mathbb {Z}_{\geq p}$ which contradicts ![]() $P \neq 0$. Now assume that
$P \neq 0$. Now assume that ![]() $k_1k_2 <0$. We cannot use the same argument as above as the coefficients
$k_1k_2 <0$. We cannot use the same argument as above as the coefficients ![]() $c_k$ are now potentially infinite power series in
$c_k$ are now potentially infinite power series in ![]() $a$. We still have that for all
$a$. We still have that for all ![]() $x \in A(|a|_v,R) = \{z \in \overline {K_v}; |a|_v<|z|< R \}$ there exists
$x \in A(|a|_v,R) = \{z \in \overline {K_v}; |a|_v<|z|< R \}$ there exists ![]() $y\in D^{*}$ satisfying
$y\in D^{*}$ satisfying
We make the substitution ![]() $x_1^{d} = x, y_1^{d} = y$ and we find that for all
$x_1^{d} = x, y_1^{d} = y$ and we find that for all ![]() $x_1 \in A^{d}$, where
$x_1 \in A^{d}$, where
there exists ![]() $y_1 \in D^{*}$ satisfying
$y_1 \in D^{*}$ satisfying
Note that because ![]() $|a|_v< R^{d}, A^{d}$ contains infinitely many points. We can take a fibred product of the sets defined by (6) and (7) by setting
$|a|_v< R^{d}, A^{d}$ contains infinitely many points. We can take a fibred product of the sets defined by (6) and (7) by setting ![]() $x_1 = x$ and we obtain that for all
$x_1 = x$ and we obtain that for all ![]() $x \in A^{d}$ there exist
$x \in A^{d}$ there exist ![]() $y,z \in D^{*}$ such that
$y,z \in D^{*}$ such that
Taking the resultant ![]() $R = \text {Res}_X(P^{*}(X,Y), P^{*}(f(X), f(Z))) \in K[Y,Z]$ with respect to the variable
$R = \text {Res}_X(P^{*}(X,Y), P^{*}(f(X), f(Z))) \in K[Y,Z]$ with respect to the variable ![]() $X$ we obtain that there are infinitely many
$X$ we obtain that there are infinitely many ![]() $y,z \in D^{*}$ satisfying
$y,z \in D^{*}$ satisfying
Thus, if ![]() $k_1 -k_2 \neq 0$, there exists a transcendental number
$k_1 -k_2 \neq 0$, there exists a transcendental number ![]() $b, |b|_v < 1$ (more precisely,
$b, |b|_v < 1$ (more precisely, ![]() $b$ is a
$b$ is a ![]() $dk_1$th root of
$dk_1$th root of ![]() $\zeta _2^{(d-1)k_1}a^{(d-1)(k_1 - k_2)}$) such that
$\zeta _2^{(d-1)k_1}a^{(d-1)(k_1 - k_2)}$) such that
for infinitely many ![]() $y \in D^{*}$ and so
$y \in D^{*}$ and so ![]() $h$ is the zero function. We set
$h$ is the zero function. We set ![]() $R(\Psi (x),\Psi (y)) = \sum _{n,m \in \mathbb {Z}_{\geq 0}}r_{nm}x^{n}y^{m}$ and we find that the coefficients
$R(\Psi (x),\Psi (y)) = \sum _{n,m \in \mathbb {Z}_{\geq 0}}r_{nm}x^{n}y^{m}$ and we find that the coefficients ![]() $h_k$ of
$h_k$ of ![]() $h(x) = \sum _{k \in \mathbb {Z}}h_kx^{k}$ satisfy
$h(x) = \sum _{k \in \mathbb {Z}}h_kx^{k}$ satisfy
for some ![]() $r \in \mathbb {Z}$ depending on
$r \in \mathbb {Z}$ depending on ![]() $P^{*}$. As
$P^{*}$. As ![]() $b$ is transcendental we obtain that
$b$ is transcendental we obtain that ![]() $r_{nm}$ = 0 for all
$r_{nm}$ = 0 for all ![]() $n,m$ and so
$n,m$ and so ![]() $R$ is the 0-polynomial. It follows that the partial derivative with respect to
$R$ is the 0-polynomial. It follows that the partial derivative with respect to ![]() $X, \partial _XP =0$ identically. For example, if not, then also
$X, \partial _XP =0$ identically. For example, if not, then also ![]() $\partial _X Pf' \neq 0$ and the projection from the variety defined by
$\partial _X Pf' \neq 0$ and the projection from the variety defined by ![]() $P(X ,Y) = P(f(X), f(Z)) = 0$ to the
$P(X ,Y) = P(f(X), f(Z)) = 0$ to the ![]() $X$-coordinate would be finite to 1. However,
$X$-coordinate would be finite to 1. However, ![]() $R = 0$ implies that we can find infinitely many solutions
$R = 0$ implies that we can find infinitely many solutions ![]() $(Y,Z)$ to
$(Y,Z)$ to ![]() $P(x_0 ,Y) = P(f(x_0), f(Z)) = 0$ for at least one fixed
$P(x_0 ,Y) = P(f(x_0), f(Z)) = 0$ for at least one fixed ![]() $x_0 \in \bar {K}$.
$x_0 \in \bar {K}$.
However, if ![]() $\partial _X P = 0$ identically, then
$\partial _X P = 0$ identically, then ![]() $k_2 = 0$. This concludes the proof.
$k_2 = 0$. This concludes the proof.
4.2 Combinatorics
In this subsection we establish all the combinatorial lemmas that are needed to carry out the proof of Proposition 4.1. For ![]() $\underline {a} \in \mathbb {Z}^{2}$ and
$\underline {a} \in \mathbb {Z}^{2}$ and ![]() $N \geq 2$ we define
$N \geq 2$ we define ![]() $S_{\underline {a}} = \mathbb {Z} \underline {a} +N\mathbb {Z}^{2}$ and for
$S_{\underline {a}} = \mathbb {Z} \underline {a} +N\mathbb {Z}^{2}$ and for ![]() $c \geq 1, B_c = \{x \in \mathbb {R}^{2}; |x|_\infty \leq c\}$. Here
$c \geq 1, B_c = \{x \in \mathbb {R}^{2}; |x|_\infty \leq c\}$. Here ![]() $|\cdot |_\infty$ is the maximum norm on
$|\cdot |_\infty$ is the maximum norm on ![]() $\mathbb {R}^{2}$.
$\mathbb {R}^{2}$.
Lemma 4.2 Let ![]() $\underline {a}= (a_1,a_2) \in \mathbb {Z}^{2} \setminus \{0\}$ be such that
$\underline {a}= (a_1,a_2) \in \mathbb {Z}^{2} \setminus \{0\}$ be such that ![]() $\text {gcd}(a_1,a_2, N) = 1$ and
$\text {gcd}(a_1,a_2, N) = 1$ and ![]() $N \geq 17$. Let
$N \geq 17$. Let ![]() $c$ be any real satisfying
$c$ be any real satisfying ![]() $\frac 34 \leq c \leq 1$. There exist at least
$\frac 34 \leq c \leq 1$. There exist at least ![]() $N^{2c-1}/4$ distinct integer vectors
$N^{2c-1}/4$ distinct integer vectors ![]() $v$ in
$v$ in ![]() $S_{\underline {a}} \cap B_{N^{c}}$.
$S_{\underline {a}} \cap B_{N^{c}}$.
Proof. As ![]() $\text {gcd}(a_1, a_2,N) = 1$ the reduction of
$\text {gcd}(a_1, a_2,N) = 1$ the reduction of ![]() $\underline {a}$
$\underline {a}$ ![]() $\mod N$ has exact order
$\mod N$ has exact order ![]() $N$ in
$N$ in ![]() $\mathbb {Z}^{2}/N\mathbb {Z}^{2}$. Thus,
$\mathbb {Z}^{2}/N\mathbb {Z}^{2}$. Thus, ![]() $S_{\underline {a}} \cap [0,N)^{2}$ contains
$S_{\underline {a}} \cap [0,N)^{2}$ contains ![]() $N$ distinct elements. We can cover the box
$N$ distinct elements. We can cover the box ![]() $[0,N)^{2}$ by at most
$[0,N)^{2}$ by at most ![]() $([N/N^{c}] +1)^{2} \leq N^{2(1-c)}(1+N^{c}/N)^{2} \leq 4 N^{2(1-c)}$ boxes of side length
$([N/N^{c}] +1)^{2} \leq N^{2(1-c)}(1+N^{c}/N)^{2} \leq 4 N^{2(1-c)}$ boxes of side length ![]() $N^{c}$. Thus, there is a box of side length
$N^{c}$. Thus, there is a box of side length ![]() $N^{c}$ that contains at least
$N^{c}$ that contains at least ![]() $N^{2c -1}/4$ distinct integer vectors and translating by one fixed integer vector in this set we also find this many vectors in
$N^{2c -1}/4$ distinct integer vectors and translating by one fixed integer vector in this set we also find this many vectors in ![]() $S_{\underline {a}} \cap B_{N^{c}}$.
$S_{\underline {a}} \cap B_{N^{c}}$.
Although the previous lemma can already be used to give a new proof of Manin–Mumford in ![]() $\mathbb {G}_m^{n}$ (see [Reference SchmidtSch03]) we need to squeeze out more information out of the structure of the set
$\mathbb {G}_m^{n}$ (see [Reference SchmidtSch03]) we need to squeeze out more information out of the structure of the set ![]() $S_{\underline {a}}$.
$S_{\underline {a}}$.
Lemma 4.3 Let ![]() $\underline {a} = (a_1,a_2) \in \mathbb {Z}^{2},\ N \in \mathbb {Z}$ be such that
$\underline {a} = (a_1,a_2) \in \mathbb {Z}^{2},\ N \in \mathbb {Z}$ be such that ![]() $\text {gcd}(a_1,a_2,N) = 1$ and
$\text {gcd}(a_1,a_2,N) = 1$ and ![]() $N \geq 17$. Let
$N \geq 17$. Let ![]() $c$ be real such that
$c$ be real such that ![]() $\frac 34 \leq c \leq 1$. There exists an absolute constant
$\frac 34 \leq c \leq 1$. There exists an absolute constant ![]() $C_1 \geq 1$ such that for every real constant
$C_1 \geq 1$ such that for every real constant ![]() $C \geq 1$ there exists
$C \geq 1$ there exists ![]() $(k_1,k_2) \in \mathbb {Z}^{2},z e \in \mathbb {Z}$ such that
$(k_1,k_2) \in \mathbb {Z}^{2},z e \in \mathbb {Z}$ such that ![]() $\text {gcd}(k_1,k_2) = 1, e(k_1,k_2) \in S_{\underline {a}} \cap B_{N^{c}}$ and either
$\text {gcd}(k_1,k_2) = 1, e(k_1,k_2) \in S_{\underline {a}} \cap B_{N^{c}}$ and either ![]() $e \leq C_1C^{2}N^{1-c}$ or
$e \leq C_1C^{2}N^{1-c}$ or ![]() $|(k_1,k_2)|_\infty > C$.
$|(k_1,k_2)|_\infty > C$.
Proof. Suppose that all ![]() $w \in S_{\underline {a}} \cap B_{N^{c}}$ are equal to
$w \in S_{\underline {a}} \cap B_{N^{c}}$ are equal to ![]() $w = e(k_1,k_2)$ with
$w = e(k_1,k_2)$ with ![]() $e \in \mathbb {Z}$ and
$e \in \mathbb {Z}$ and ![]() $|(k_1,k_2)|_\infty \leq C$. Then
$|(k_1,k_2)|_\infty \leq C$. Then ![]() $S_{\underline {a}} \cap B_{N^{c}}$ is contained in the union of at most
$S_{\underline {a}} \cap B_{N^{c}}$ is contained in the union of at most ![]() $(2C +1)^{2}$
$(2C +1)^{2}$ ![]() $\mathbb {Z}$-modules
$\mathbb {Z}$-modules ![]() $\mathcal {L}_v = \{lv , l \in \mathbb {Z}\}$ of rank 1. However, the cardinality of
$\mathcal {L}_v = \{lv , l \in \mathbb {Z}\}$ of rank 1. However, the cardinality of ![]() $\mathcal {L}_v \cap B_{N^{c}} \setminus \{0\}$ is bounded by
$\mathcal {L}_v \cap B_{N^{c}} \setminus \{0\}$ is bounded by ![]() $2N^{c}/|v|_\infty$. Let
$2N^{c}/|v|_\infty$. Let ![]() $m$ be the minimum of
$m$ be the minimum of ![]() $|v|_\infty$ as
$|v|_\infty$ as ![]() $v$ runs through
$v$ runs through ![]() $v$ such that
$v$ such that ![]() $\mathcal {L}_v \cap B_{N^{c}}\cap S_{\underline {a}} \neq \{0\}$. From Lemma 4.2 follows
$\mathcal {L}_v \cap B_{N^{c}}\cap S_{\underline {a}} \neq \{0\}$. From Lemma 4.2 follows
and so ![]() $m \leq C_1C^{2} N^{1-c}$. This finishes the proof.
$m \leq C_1C^{2} N^{1-c}$. This finishes the proof.
We record the following, whose proof is given in [Reference SchmidtSch03].
Lemma 4.4 Let ![]() $k \geq 2$ be a rational integers and
$k \geq 2$ be a rational integers and ![]() $f = \text {gcd}(N,k)$. There exists an integer
$f = \text {gcd}(N,k)$. There exists an integer ![]() $\ell$ such that
$\ell$ such that
Now we apply what we established combinatorially to roots of unity.
Lemma 4.5 Fix constants ![]() $C \geq 1$ and
$C \geq 1$ and ![]() $3/4 \leq c \leq 1$. Let
$3/4 \leq c \leq 1$. Let ![]() $(\zeta _1, \zeta _2)$ be a point of order
$(\zeta _1, \zeta _2)$ be a point of order ![]() $N \geq 17$ in
$N \geq 17$ in ![]() $\mathbb {G}_m^{2}$. There exists a primitive
$\mathbb {G}_m^{2}$. There exists a primitive ![]() $N$th root of unity
$N$th root of unity ![]() $\zeta$ and integers
$\zeta$ and integers ![]() $k_1$,
$k_1$, ![]() $k_2$,
$k_2$, ![]() $e$ such that
$e$ such that ![]() $\text {gcd}(k_1,k_2) = 1$,
$\text {gcd}(k_1,k_2) = 1$, ![]() $|(k_1,k_2)|_\infty \leq N^{c}/e$ and
$|(k_1,k_2)|_\infty \leq N^{c}/e$ and ![]() $(\zeta _1, \zeta _2) = (\zeta _e^{(1)}\zeta _N^{k_1}, \zeta _e^{(2)}\zeta _N^{k_2})$ where
$(\zeta _1, \zeta _2) = (\zeta _e^{(1)}\zeta _N^{k_1}, \zeta _e^{(2)}\zeta _N^{k_2})$ where ![]() $\zeta _e^{(1)}$,
$\zeta _e^{(1)}$, ![]() $\zeta _e^{(2)}$ are
$\zeta _e^{(2)}$ are ![]() $e$th roots of
$e$th roots of ![]() $1$. Moreover, either
$1$. Moreover, either ![]() $e \leq C_1C^{2} N^{1-c }$ or
$e \leq C_1C^{2} N^{1-c }$ or ![]() $|(k_1,k_2)|_\infty > C$ for an absolute constant
$|(k_1,k_2)|_\infty > C$ for an absolute constant ![]() $C_1$ independent of
$C_1$ independent of ![]() $C$ and
$C$ and ![]() $N$.
$N$.
Proof. There exists an integer vector ![]() $\underline {a} = (a_1, a_2)$ with the property
$\underline {a} = (a_1, a_2)$ with the property ![]() $\text {gcd}(a_1,a_2,N) = 1$ such that
$\text {gcd}(a_1,a_2,N) = 1$ such that ![]() $(\zeta _1, \zeta _2) = (\zeta _N^{a_1}, \zeta _N^{a_2})$ for a primitive
$(\zeta _1, \zeta _2) = (\zeta _N^{a_1}, \zeta _N^{a_2})$ for a primitive ![]() $N$th root of unity
$N$th root of unity ![]() $\zeta _N$. Applying Lemma 4.3 we find
$\zeta _N$. Applying Lemma 4.3 we find ![]() $(k_1, k_2), e$ as in the statement as well as an integer
$(k_1, k_2), e$ as in the statement as well as an integer ![]() $k$ such that
$k$ such that ![]() $k(a_1, a_2) = e(k_1,k_2)\ {\rm mod}\ N$. By Lemma 4.4 we can replace
$k(a_1, a_2) = e(k_1,k_2)\ {\rm mod}\ N$. By Lemma 4.4 we can replace ![]() $k$ by
$k$ by ![]() $f\ell$ where
$f\ell$ where ![]() $f = \text {gcd}(k,N)$ and
$f = \text {gcd}(k,N)$ and ![]() $\ell$ is invertible
$\ell$ is invertible ![]() ${\rm mod}\ N$. As
${\rm mod}\ N$. As ![]() $k_1,k_2$ are co-prime we deduce that
$k_1,k_2$ are co-prime we deduce that ![]() $f|e$. Denoting by
$f|e$. Denoting by ![]() $\ell ^{*}$ the inverse of
$\ell ^{*}$ the inverse of ![]() $\ell \mod N$ we can replace
$\ell \mod N$ we can replace ![]() $\zeta _N$ by
$\zeta _N$ by ![]() $\zeta _N^{\ell ^{*}}$ and obtain the lemma.
$\zeta _N^{\ell ^{*}}$ and obtain the lemma.
4.3 Zero-counting
In this subsection we briefly recall the main counting results over ![]() $p$-adic fields. They are consequences of a careful study of Newton polygons and all proofs can be found in the notes in [Reference CherryChe09]. We recall that
$p$-adic fields. They are consequences of a careful study of Newton polygons and all proofs can be found in the notes in [Reference CherryChe09]. We recall that ![]() $K_v$ is a completion of
$K_v$ is a completion of ![]() $K$ with respect to a non-archimedean place
$K$ with respect to a non-archimedean place ![]() $v$ and we let
$v$ and we let ![]() $g(z) = \sum _{n \in \mathbb {Z}}a_nz^{n}, a_n \in K_v$ (
$g(z) = \sum _{n \in \mathbb {Z}}a_nz^{n}, a_n \in K_v$ (![]() $g \in \mathcal {A}[r_1,r_2$)) be a power series defining a non-constant analytic function on an annulus
$g \in \mathcal {A}[r_1,r_2$)) be a power series defining a non-constant analytic function on an annulus
for real ![]() $0< r_1 < r_2$. We define
$0< r_1 < r_2$. We define
(counting with multiplicity) as well as
We then define
We need the following lemma [Reference CherryChe09, Theorem 2.5.1] which is central to our arguments.
Lemma 4.6 (Poisson–Jensen)
With ![]() $g$ as above, it holds that
$g$ as above, it holds that
4.4 Lower bounds
In this short subsection we record the Galois lower bounds that are valid for roots of unity over completions of number fields. As usual ![]() $K_v$ is a completion of
$K_v$ is a completion of ![]() $K$ with respect to a non-archimedean place
$K$ with respect to a non-archimedean place ![]() $v$ of
$v$ of ![]() $K$.
$K$.
Lemma 4.7 Let ![]() $N$ be a positive integer dividing a power of
$N$ be a positive integer dividing a power of ![]() $d$ and
$d$ and ![]() $\zeta _N$ a primitive
$\zeta _N$ a primitive ![]() $N$th root of
$N$th root of ![]() $1$. There exists a positive real number
$1$. There exists a positive real number ![]() $C_G$ depending on
$C_G$ depending on ![]() $v$,
$v$, ![]() $d$,
$d$, ![]() $K$ such that
$K$ such that
Proof. This follows from Corollary 6.5 in [Reference Boxall, Jones and SchmidtBJS22].
4.5 Auxiliary function
In what follows, we assume that ![]() $\mathcal {C}$ is not special. We switch coordinates first. If the curve
$\mathcal {C}$ is not special. We switch coordinates first. If the curve ![]() $\mathcal {C}$ is given by affine coordinates
$\mathcal {C}$ is given by affine coordinates ![]() $(X_1, X_2)$ we switch to coordinates
$(X_1, X_2)$ we switch to coordinates ![]() $(X,Y) = (1/X_1,1/X_2)$ and denote by
$(X,Y) = (1/X_1,1/X_2)$ and denote by ![]() $P \in \mathcal {O}_K[X,Y]$ the absolutely irreducible polynomial defining
$P \in \mathcal {O}_K[X,Y]$ the absolutely irreducible polynomial defining ![]() $\mathcal {C}$ in these coordinates. We then set
$\mathcal {C}$ in these coordinates. We then set
For a tuple ![]() $\underline {s}= (\zeta _1, \zeta _2, k_1,k_2, \beta )$ where
$\underline {s}= (\zeta _1, \zeta _2, k_1,k_2, \beta )$ where ![]() $\zeta _1, \zeta _2$ are roots of unity of order
$\zeta _1, \zeta _2$ are roots of unity of order ![]() $e$ dividing some power of
$e$ dividing some power of ![]() $d$ and
$d$ and ![]() $k_1,k_2$ are co-prime rational integers satisfying
$k_1,k_2$ are co-prime rational integers satisfying ![]() $k_1 > 0, k_1 \geq k_2$ and
$k_1 > 0, k_1 \geq k_2$ and ![]() $\beta \in \mathcal {O}_\alpha$ we define
$\beta \in \mathcal {O}_\alpha$ we define ![]() $\nu = \nu _{\underline {s}}$ by
$\nu = \nu _{\underline {s}}$ by
where ![]() $\phi = \Phi (\beta )$ and
$\phi = \Phi (\beta )$ and ![]() $b_k$ is given by
$b_k$ is given by
We note that ![]() $b_k$ does not necessarily lie in
$b_k$ does not necessarily lie in ![]() $\bar {K}$ but in
$\bar {K}$ but in ![]() $\bar {K}_v$. Moreover, the function
$\bar {K}_v$. Moreover, the function ![]() $\nu$ is an analytic function on the annulus
$\nu$ is an analytic function on the annulus ![]() $A[1,r)$ where
$A[1,r)$ where ![]() $r = R/|\phi |_v^{1/{|(k_1,k_2)|_\infty }}$. Note that we have
$r = R/|\phi |_v^{1/{|(k_1,k_2)|_\infty }}$. Note that we have ![]() $|\nu |_v \leq 1$.
$|\nu |_v \leq 1$.
Now we proceed to bounding ![]() $r$ and
$r$ and ![]() $|\nu |_1$ from below. We first prove these bounds up to finitely many possibilities for
$|\nu |_1$ from below. We first prove these bounds up to finitely many possibilities for ![]() $\beta \in \mathcal {O}_\alpha$.
$\beta \in \mathcal {O}_\alpha$.
Lemma 4.8 There exists a constant ![]() $C_{O}$ depending only on
$C_{O}$ depending only on ![]() $\mathcal {C}$ such that if
$\mathcal {C}$ such that if ![]() $|\phi |_v < C_O$ and
$|\phi |_v < C_O$ and ![]() $k_1 \neq k_2$, then
$k_1 \neq k_2$, then
for positive constants ![]() $C_2, C_3$ depending only on
$C_2, C_3$ depending only on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Recall our convention that ![]() $k_1 > 0$ and
$k_1 > 0$ and ![]() $k_1 \geq k_2$. Let
$k_1 \geq k_2$. Let ![]() $(n_0,m_0)$ be a pair of positive integers such that
$(n_0,m_0)$ be a pair of positive integers such that ![]() $a_{nm}\neq 0$ and
$a_{nm}\neq 0$ and ![]() $n +m$ is minimal with this property. Note that there are at most finitely many such pairs. Let
$n +m$ is minimal with this property. Note that there are at most finitely many such pairs. Let ![]() $k_0 = k_1n_0 + k_2m_0$ and first suppose there exists another pair of positive integers
$k_0 = k_1n_0 + k_2m_0$ and first suppose there exists another pair of positive integers ![]() $(n_1,m_1) \neq (n_0,m_0)$ such that
$(n_1,m_1) \neq (n_0,m_0)$ such that ![]() $k_1n_1 + k_2m_1 = k_0$ and
$k_1n_1 + k_2m_1 = k_0$ and ![]() $|a_{n_0m_0}\phi ^{n_0 + m_0}|_v \leq |a_{n_1m_1}\phi ^{n_1 + m_1}|_v$. Then
$|a_{n_0m_0}\phi ^{n_0 + m_0}|_v \leq |a_{n_1m_1}\phi ^{n_1 + m_1}|_v$. Then ![]() $|a_{n_0m_0}|_v \leq |\phi |^{k_1 - k_2}_v$ and by our assumption
$|a_{n_0m_0}|_v \leq |\phi |^{k_1 - k_2}_v$ and by our assumption ![]() $k_1- k_2 > 0$. Thus, if
$k_1- k_2 > 0$. Thus, if ![]() $|\phi |_v < |a_{n_0m_0}|$, no such pair
$|\phi |_v < |a_{n_0m_0}|$, no such pair ![]() $(n_1,n_2)$ exists and it follows that
$(n_1,n_2)$ exists and it follows that ![]() $|b_{k_0}|_v = |a_{n_0m_0}\phi ^{n_0 + m_0}|_v$. As
$|b_{k_0}|_v = |a_{n_0m_0}\phi ^{n_0 + m_0}|_v$. As ![]() $|b_{k_0}| \leq |\nu |_1$ the lemma follows.
$|b_{k_0}| \leq |\nu |_1$ the lemma follows.
From this point onward we may assume that ![]() $\beta = f^{\circ m}(\alpha )$ for
$\beta = f^{\circ m}(\alpha )$ for ![]() $m$ bounded by a constant only depending on
$m$ bounded by a constant only depending on ![]() $\mathcal {C}$. However, we indicate when we make use of this fact.
$\mathcal {C}$. However, we indicate when we make use of this fact.
Lemma 4.9 There exists a constant ![]() $C_{{\rm lower}} = C_{{\rm lower}}(\alpha,\mathcal {C}) \geq 2$ such that if
$C_{{\rm lower}} = C_{{\rm lower}}(\alpha,\mathcal {C}) \geq 2$ such that if ![]() $|(k_1,k_2)|_\infty \geq C_{{\rm lower}}$, then
$|(k_1,k_2)|_\infty \geq C_{{\rm lower}}$, then
for positive constants ![]() $C_2, C_3$ depending only on
$C_2, C_3$ depending only on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Let ![]() $(n_0,m_0)$ be, as in the previous lemma, a pair of positive integers such that
$(n_0,m_0)$ be, as in the previous lemma, a pair of positive integers such that ![]() $a_{nm}\neq 0$ and
$a_{nm}\neq 0$ and ![]() $n +m$ is minimal with this property and again suppose that there exists another pair of positive integers
$n +m$ is minimal with this property and again suppose that there exists another pair of positive integers ![]() $(n_1,m_1) \neq (n_0,m_0)$ such that
$(n_1,m_1) \neq (n_0,m_0)$ such that ![]() $k_1n_1 + k_2m_1 = k_0$ and
$k_1n_1 + k_2m_1 = k_0$ and ![]() $|a_{n_0m_0}\phi ^{n_0 + m_0}|_v \leq |a_{n_1m_1}\phi ^{n_1 + m_1}|_v$.
$|a_{n_0m_0}\phi ^{n_0 + m_0}|_v \leq |a_{n_1m_1}\phi ^{n_1 + m_1}|_v$.
We first prove that if ![]() $k_1 \neq k_2$, then
$k_1 \neq k_2$, then ![]() $|k_1 - k_2| \geq c_1|(k_1,k_2)|_\infty$ where
$|k_1 - k_2| \geq c_1|(k_1,k_2)|_\infty$ where ![]() $c_1 >0$ is a constant only depending on
$c_1 >0$ is a constant only depending on ![]() $\mathcal {C}$.
$\mathcal {C}$.
If ![]() $k_1k_2 <0$, this is trivial and we can set
$k_1k_2 <0$, this is trivial and we can set ![]() $c_1 =1$. If
$c_1 =1$. If ![]() $k_1k_2 >0$, we note that
$k_1k_2 >0$, we note that ![]() $(n_1 -n_0, m_1 -m_0) \in \mathbb {Z}(-k_2,k_1)$ and so either
$(n_1 -n_0, m_1 -m_0) \in \mathbb {Z}(-k_2,k_1)$ and so either ![]() $n_1 -n_0 \leq 0$ or
$n_1 -n_0 \leq 0$ or ![]() $m_1 - m_0 \leq 0$. If
$m_1 - m_0 \leq 0$. If ![]() $n_1 - n_0 \leq 0$, then
$n_1 - n_0 \leq 0$, then ![]() $n_1 -n_0 \leq -k_2$ and as
$n_1 -n_0 \leq -k_2$ and as ![]() $k_2 >0$ we deduce
$k_2 >0$ we deduce ![]() $k_2 \leq n_0$. Similarly, if
$k_2 \leq n_0$. Similarly, if ![]() $m_1 -m_0 \leq 0$ we deduce that
$m_1 -m_0 \leq 0$ we deduce that ![]() $k_1 \leq m_0$. In either case, we have that
$k_1 \leq m_0$. In either case, we have that ![]() $|2(k_1-k_2)(n_0,m_0)|_\infty \geq |(k_1, k_2)|_\infty$.
$|2(k_1-k_2)(n_0,m_0)|_\infty \geq |(k_1, k_2)|_\infty$.
We continue by noting as in the previous lemma that ![]() $|\phi |_v^{k_1-k_2} \geq |a_{n_0m_0}|_v$. Thus, if
$|\phi |_v^{k_1-k_2} \geq |a_{n_0m_0}|_v$. Thus, if ![]() $k_1 -k_2 > \log |a_{n_0m_0}|_v/\!\log |\phi |_v$, then we cannot find
$k_1 -k_2 > \log |a_{n_0m_0}|_v/\!\log |\phi |_v$, then we cannot find ![]() $(n_1,n_2)$ as previously. We deduce from the non-archimedean triangle inequality and what we just proved that if
$(n_1,n_2)$ as previously. We deduce from the non-archimedean triangle inequality and what we just proved that if ![]() $|(k_1,k_2)|_\infty > c_1^{-1}\log |a_{n_0m_0}|_v/\!\log |\phi |_v$, then
$|(k_1,k_2)|_\infty > c_1^{-1}\log |a_{n_0m_0}|_v/\!\log |\phi |_v$, then ![]() $|b_{k_0}|_v = |a_{n_0m_0} \phi ^{n_0 + m_0}|_v$ and we are finished.
$|b_{k_0}|_v = |a_{n_0m_0} \phi ^{n_0 + m_0}|_v$ and we are finished.
In the next two lemmas we are going to use the fact that we can concentrate on a finite subset of ![]() $\mathcal {O}_\alpha$ which is reflected in a bound for the height.
$\mathcal {O}_\alpha$ which is reflected in a bound for the height.
Lemma 4.10 Suppose that ![]() $|(k_1,k_2)|_\infty \leq C_1$ and
$|(k_1,k_2)|_\infty \leq C_1$ and ![]() $h(\beta ) \leq C_1$ for some positive constant
$h(\beta ) \leq C_1$ for some positive constant ![]() $C_1$. Then either
$C_1$. Then either
for ![]() $C_2 = C_2(C_1,\mathcal {C}, \alpha )$ or
$C_2 = C_2(C_1,\mathcal {C}, \alpha )$ or ![]() $\text {ord}(\zeta _1^{-k_2}\zeta _2^{k_1}) \leq C_3(\alpha,\mathcal {C})$.
$\text {ord}(\zeta _1^{-k_2}\zeta _2^{k_1}) \leq C_3(\alpha,\mathcal {C})$.
Proof. (First note that ![]() $e \neq \exp (1)$). Set
$e \neq \exp (1)$). Set ![]() $x_0 = \zeta _1^{-1/k_1}$ where we pick a
$x_0 = \zeta _1^{-1/k_1}$ where we pick a ![]() $k_1$th root such that the order of
$k_1$th root such that the order of ![]() $x_0$ still divides a power of
$x_0$ still divides a power of ![]() $d$. This can be done by writing
$d$. This can be done by writing ![]() $k_1 =k\tilde {k}$ with
$k_1 =k\tilde {k}$ with ![]() $k$ dividing a power of
$k$ dividing a power of ![]() $d$ and
$d$ and ![]() $\tilde {k}$ co-prime to
$\tilde {k}$ co-prime to ![]() $d$. We can write
$d$. We can write ![]() $\zeta _1 = \zeta _2^{\tilde {k}}$ with
$\zeta _1 = \zeta _2^{\tilde {k}}$ with ![]() $\zeta _2$ having the same order as
$\zeta _2$ having the same order as ![]() $\zeta _1$ and then pick any
$\zeta _1$ and then pick any ![]() $k$th root of
$k$th root of ![]() $\zeta _2$. We obtain
$\zeta _2$. We obtain ![]() $\nu (x_0) = P(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi ))$. Now if
$\nu (x_0) = P(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi ))$. Now if ![]() $\nu (x_0) = 0$, then the degree
$\nu (x_0) = 0$, then the degree ![]() $[K_v(\zeta _2\zeta _1^{-k_2/k_1}):K_v] \leq \deg (\mathcal {C})$ because otherwise we can let
$[K_v(\zeta _2\zeta _1^{-k_2/k_1}):K_v] \leq \deg (\mathcal {C})$ because otherwise we can let ![]() $\text {Gal}(\overline {K_v}/K_v)$ act on the point
$\text {Gal}(\overline {K_v}/K_v)$ act on the point ![]() $(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi )$ and find more than
$(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi )$ and find more than ![]() $\deg (\mathcal {C})$ points on
$\deg (\mathcal {C})$ points on ![]() $\mathcal {C}$ with
$\mathcal {C}$ with ![]() $X$-coordinate equal to
$X$-coordinate equal to ![]() $\beta$. This would imply that
$\beta$. This would imply that ![]() $\mathcal {C}$ is special. Thus,
$\mathcal {C}$ is special. Thus, ![]() $\text {ord}(\zeta _2^{k_1}\zeta _1^{-k_2})$ is bounded as in the statement.
$\text {ord}(\zeta _2^{k_1}\zeta _1^{-k_2})$ is bounded as in the statement.
Now suppose that ![]() $\nu (x_0) \neq 0$. We note that the point
$\nu (x_0) \neq 0$. We note that the point ![]() $(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi ))$ is algebraic of degree at most
$(\beta, \Psi (\zeta _2\zeta _1^{-k_2/k_1}\phi ))$ is algebraic of degree at most ![]() $|e(k_1,k_2)|_\infty ^{\log d/\!\log 2}$ over
$|e(k_1,k_2)|_\infty ^{\log d/\!\log 2}$ over ![]() $K$ as
$K$ as ![]() $|e(k_1,k_2)|_\infty$ is a bound on the order of
$|e(k_1,k_2)|_\infty$ is a bound on the order of ![]() $\zeta _2\zeta _1^{-k_2/k_1}$ and so
$\zeta _2\zeta _1^{-k_2/k_1}$ and so
with ![]() $d^{n} \leq |e(k_1,k_2 )|_\infty ^{\log d/\!\log 2}$. Thus,
$d^{n} \leq |e(k_1,k_2 )|_\infty ^{\log d/\!\log 2}$. Thus, ![]() $H(\nu (x_0))\leq c_1c_2^{e^{{\log d}/{\log 2}}}$ for constants
$H(\nu (x_0))\leq c_1c_2^{e^{{\log d}/{\log 2}}}$ for constants ![]() $c_1,c_2$ depending only on
$c_1,c_2$ depending only on ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\alpha$ and we deduce the inequality (10) from the standard
$\alpha$ and we deduce the inequality (10) from the standard ![]() $|y_0|_v \geq H(y_0)^{-[\mathbb {Q}(y_0):\mathbb {Q}]}$ that is valid for any algebraic point
$|y_0|_v \geq H(y_0)^{-[\mathbb {Q}(y_0):\mathbb {Q}]}$ that is valid for any algebraic point ![]() $y_0$.
$y_0$.
Lemma 4.11 Suppose that ![]() $\text {ord}(\zeta _1^{-k_2}\zeta _2^{k_1}) \leq C_1, h(\beta ) \leq C_1$ and
$\text {ord}(\zeta _1^{-k_2}\zeta _2^{k_1}) \leq C_1, h(\beta ) \leq C_1$ and ![]() $|(k_1, k_2)|_\infty \leq C_1$ for some constant
$|(k_1, k_2)|_\infty \leq C_1$ for some constant ![]() $C_1$ and that
$C_1$ and that ![]() $\nu$ is not the zero function. Then
$\nu$ is not the zero function. Then
for a positive constant ![]() $C_2 = C_2(C_1, \mathcal {C},\alpha )$.
$C_2 = C_2(C_1, \mathcal {C},\alpha )$.
Proof. We first note that there are only a finite number of possibilities for ![]() $\beta$ as the height of
$\beta$ as the height of ![]() $\beta$ is bounded. There are also only a finite number of possibilities for
$\beta$ is bounded. There are also only a finite number of possibilities for ![]() $k_1,k_2$. For each
$k_1,k_2$. For each ![]() $k$ we can choose
$k$ we can choose ![]() $(n_k,m_k)$ such that
$(n_k,m_k)$ such that ![]() $k_1n_k + k_2m_k = k$ and factor out
$k_1n_k + k_2m_k = k$ and factor out ![]() $\zeta _1^{n_k}\zeta _2^{m_k}$. Note that for each
$\zeta _1^{n_k}\zeta _2^{m_k}$. Note that for each ![]() $k$ the choice of
$k$ the choice of ![]() $(n_k,m_k)$ only depends on
$(n_k,m_k)$ only depends on ![]() $k_1,k_2$. Now we see that
$k_1,k_2$. Now we see that ![]() $b_k = \zeta _1^{n_k}\zeta _2^{m_k}\tilde {b}_k$ for
$b_k = \zeta _1^{n_k}\zeta _2^{m_k}\tilde {b}_k$ for ![]() $\tilde {b}_k$ only depending on
$\tilde {b}_k$ only depending on ![]() $\beta, k_1,k_2$ and
$\beta, k_1,k_2$ and ![]() $\zeta _1^{-k_2}\zeta _2^{k_1}$. It follows that if
$\zeta _1^{-k_2}\zeta _2^{k_1}$. It follows that if ![]() $\beta, k_1,k_2, \zeta _1^{-k_2}\zeta _2^{k_1}$ vary in a finite set, the sequence
$\beta, k_1,k_2, \zeta _1^{-k_2}\zeta _2^{k_1}$ vary in a finite set, the sequence ![]() $(|b_k|_v)_{k\in \mathbb {Z}}$ varies in a finite set. Thus,
$(|b_k|_v)_{k\in \mathbb {Z}}$ varies in a finite set. Thus, ![]() $|\nu _{\underline {s}}|_1$ varies in a finite set and as
$|\nu _{\underline {s}}|_1$ varies in a finite set and as ![]() $|\nu |_1 >0$ we get an absolute lower bound for
$|\nu |_1 >0$ we get an absolute lower bound for ![]() $|\nu |_1$.
$|\nu |_1$.
Lemma 4.12 Suppose that ![]() $\nu$ as above (8) is not the zero function. It holds that
$\nu$ as above (8) is not the zero function. It holds that
Proof. If ![]() $k_1k_2 > 0$, then
$k_1k_2 > 0$, then ![]() $b_k = 0$ for
$b_k = 0$ for ![]() $k<0$ and the statement becomes trivial. Thus, we may and do assume that
$k<0$ and the statement becomes trivial. Thus, we may and do assume that ![]() $k_1k_2<0$. From the expansion of
$k_1k_2<0$. From the expansion of ![]() $b_k$ (9) we deduce that
$b_k$ (9) we deduce that ![]() $|b_k|_v \leq |\phi |_v^{\ell _k}$ where
$|b_k|_v \leq |\phi |_v^{\ell _k}$ where ![]() $\ell _k$ is defined by
$\ell _k$ is defined by ![]() $\ell _k = \min _{m,n \in \mathbb {Z}_{\geq 0}}\{m + n; k_1m + k_2n = k\}$. As
$\ell _k = \min _{m,n \in \mathbb {Z}_{\geq 0}}\{m + n; k_1m + k_2n = k\}$. As ![]() $|k| \leq |(k_1,k_2)|_\infty \ell _k$ we see that for
$|k| \leq |(k_1,k_2)|_\infty \ell _k$ we see that for ![]() $\kappa = \kappa (\nu,1)$ holds
$\kappa = \kappa (\nu,1)$ holds ![]() $|\nu |_1 \leq |\phi |_v^{|\kappa |/|(k_1,k_2)|_\infty }$ and the lemma follows.
$|\nu |_1 \leq |\phi |_v^{|\kappa |/|(k_1,k_2)|_\infty }$ and the lemma follows.
4.6 Transcendence
In this subsection we record a transcendence result that belongs to the circle of classical transcendence results on Mahler functions. It is crucial for the application of Theorem 7 to the proof of Theorem 1.
As a direct consequence of work of Nishioka or Corvaja and Zannier we obtain the following theorem.
Theorem 8 (Nishioka)
Let ![]() $f \in K[X]$ be a non-exceptional polynomial. For
$f \in K[X]$ be a non-exceptional polynomial. For ![]() $\alpha \in D_{v}^{*}\cap \bar {\mathbb {Q}}$,
$\alpha \in D_{v}^{*}\cap \bar {\mathbb {Q}}$, ![]() $\Psi (\alpha )$ is transcendental.
$\Psi (\alpha )$ is transcendental.
Proof. From [Reference Becker and BergweilerBB93, Theorem 1] follows that ![]() $\Psi$ is not an algebraic function. Now for
$\Psi$ is not an algebraic function. Now for ![]() $v$ an archimedean place the present lemma follows from a theorem of Nishioka (see, for example, [Reference NishiokaNis96, Corollary of Theorem 1.5.1]). For a non-archimedean place we could perhaps trace the steps of Nishioka's proof and prove it in the non-archimedean case. However, it also follows almost directly from a result of Corvaja and Zannier [Reference Corvaja and ZannierCZ02].
$v$ an archimedean place the present lemma follows from a theorem of Nishioka (see, for example, [Reference NishiokaNis96, Corollary of Theorem 1.5.1]). For a non-archimedean place we could perhaps trace the steps of Nishioka's proof and prove it in the non-archimedean case. However, it also follows almost directly from a result of Corvaja and Zannier [Reference Corvaja and ZannierCZ02].
Namely, if ![]() $\Psi (\alpha )$ is algebraic we have that
$\Psi (\alpha )$ is algebraic we have that ![]() $\Psi (\alpha ^{d^{n}}) = f^{\circ n}(\Psi (\alpha ))$ lies in the same field. We then apply Theorem 1 of their paper to the function
$\Psi (\alpha ^{d^{n}}) = f^{\circ n}(\Psi (\alpha ))$ lies in the same field. We then apply Theorem 1 of their paper to the function ![]() $\Psi (R^{v} z)$ and
$\Psi (R^{v} z)$ and ![]() $z_{d^{n}} = (R^{v})^{-1}\alpha ^{d^{n}}$.
$z_{d^{n}} = (R^{v})^{-1}\alpha ^{d^{n}}$.
4.7 Proof of Proposition 4.1
Recall that we assume that ![]() $|\Phi (\alpha )|_v < (R^{v})^{d}$. From Theorem 8 follows that
$|\Phi (\alpha )|_v < (R^{v})^{d}$. From Theorem 8 follows that ![]() $\Phi (\beta )$ is a transcendental number for all
$\Phi (\beta )$ is a transcendental number for all ![]() $\beta \in \mathcal {O}_\alpha$. We start with a solution
$\beta \in \mathcal {O}_\alpha$. We start with a solution ![]() $(\beta _1, \beta _2) \in \mathcal {S}_\beta ^{2} \cap \mathcal {C}$ and let
$(\beta _1, \beta _2) \in \mathcal {S}_\beta ^{2} \cap \mathcal {C}$ and let ![]() $n$ be minimal such that
$n$ be minimal such that ![]() $f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2) = f^{\circ n}(\beta )$. We then have that
$f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2) = f^{\circ n}(\beta )$. We then have that
where ![]() $(\zeta _1, \zeta _2) \in \mathbb {G}_m^{2}$ is of order
$(\zeta _1, \zeta _2) \in \mathbb {G}_m^{2}$ is of order ![]() $N$ dividing
$N$ dividing ![]() $d^{n}$ and it holds that
$d^{n}$ and it holds that ![]() $2^{n} \leq N$. Thus, we may assume that
$2^{n} \leq N$. Thus, we may assume that ![]() $N \geq 17$, because we are finished otherwise. Let
$N \geq 17$, because we are finished otherwise. Let ![]() $C_{\text {lower}}$ be the constant from Lemma 4.9.
$C_{\text {lower}}$ be the constant from Lemma 4.9.
We set ![]() $c = 1- ({\log 2})/({4\log d})$ and employing Lemma 4.5 we set
$c = 1- ({\log 2})/({4\log d})$ and employing Lemma 4.5 we set ![]() $(\zeta _1, \zeta _2) = (\zeta _e^{(1)}\zeta _N^{k_1}, \zeta _e^{(2)}\zeta _N^{k_2})$, where
$(\zeta _1, \zeta _2) = (\zeta _e^{(1)}\zeta _N^{k_1}, \zeta _e^{(2)}\zeta _N^{k_2})$, where ![]() $\zeta _N$ is a primitive
$\zeta _N$ is a primitive ![]() $N$th root of unity,
$N$th root of unity, ![]() $\zeta _e^{(1)}, \zeta _e^{(2)}$ are
$\zeta _e^{(1)}, \zeta _e^{(2)}$ are ![]() $e$th roots of unity (with
$e$th roots of unity (with ![]() $e$ dividing
$e$ dividing ![]() $N$), and
$N$), and ![]() $|(k_1, k_2)|_\infty \leq N^{c}/e$. Moreover, either
$|(k_1, k_2)|_\infty \leq N^{c}/e$. Moreover, either ![]() $|(k_1, k_2)|_\infty > C_{\text {lower}}$ or
$|(k_1, k_2)|_\infty > C_{\text {lower}}$ or ![]() $e \leq C_\text {upper}N^{ 1 - c}$ for a constant
$e \leq C_\text {upper}N^{ 1 - c}$ for a constant ![]() $C_\text {upper}$ depending only on
$C_\text {upper}$ depending only on ![]() $\mathcal {C}, \alpha$. We set
$\mathcal {C}, \alpha$. We set ![]() $\nu = \nu _{\underline {s}}$, where
$\nu = \nu _{\underline {s}}$, where ![]() $\underline {s} = (\zeta _e^{(1)}, \zeta _e^{(2)}, k_1,k_2)$.
$\underline {s} = (\zeta _e^{(1)}, \zeta _e^{(2)}, k_1,k_2)$.
If ![]() $k_1 = 0$, then
$k_1 = 0$, then ![]() $\text {Gal}(K_v (\zeta _N)/K_v(\zeta _e^{(1)}))$ fixes
$\text {Gal}(K_v (\zeta _N)/K_v(\zeta _e^{(1)}))$ fixes ![]() $\beta _1$ whereas the Galois orbit of
$\beta _1$ whereas the Galois orbit of ![]() $\beta _2$ is bounded from below by
$\beta _2$ is bounded from below by ![]() $(C_G/C_{\rm upper})N^{c}$. Hence,
$(C_G/C_{\rm upper})N^{c}$. Hence, ![]() $N$ and also
$N$ and also ![]() $n$ are bounded unless
$n$ are bounded unless ![]() $\mathcal {C}$ is special. Similarly if
$\mathcal {C}$ is special. Similarly if ![]() $k_2 = 0$. Now if
$k_2 = 0$. Now if ![]() $k_1 =k_2$, then
$k_1 =k_2$, then ![]() $f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2)$ for
$f^{\circ n}(\beta _1) = f^{\circ n}(\beta _2)$ for ![]() $n$ such that
$n$ such that ![]() $d^{n} \leq e^{\log d/\!\log 2} \leq C_d N^{1/4}$ (
$d^{n} \leq e^{\log d/\!\log 2} \leq C_d N^{1/4}$ (![]() ${C_d = C_{\text {upper}}^{\log d/\!\log 2}}$). We deduce that the Galois orbit of
${C_d = C_{\text {upper}}^{\log d/\!\log 2}}$). We deduce that the Galois orbit of ![]() $(\beta _1, \beta _2)$ is contained in the intersection of
$(\beta _1, \beta _2)$ is contained in the intersection of ![]() $\mathcal {C}$ and the curve of degree
$\mathcal {C}$ and the curve of degree ![]() $d^{n}$ defined by
$d^{n}$ defined by ![]() $f^{\circ n}(X) -f^{\circ n}(Y) = 0$. Now the Galois orbit is bounded from below
$f^{\circ n}(X) -f^{\circ n}(Y) = 0$. Now the Galois orbit is bounded from below ![]() $C_GN$ and, thus, it follows from Bézout's theorem that
$C_GN$ and, thus, it follows from Bézout's theorem that ![]() $N$ is bounded unless
$N$ is bounded unless ![]() $\mathcal {C}$ is a component of
$\mathcal {C}$ is a component of ![]() $f^{\circ n}(X) - f^{\circ n}(Y) = 0$ and, thus, special.
$f^{\circ n}(X) - f^{\circ n}(Y) = 0$ and, thus, special.
From this point on we assume that ![]() $\mathcal {C}$ is not special and
$\mathcal {C}$ is not special and ![]() $k_1k_2(k_1-k_2) \neq 0$. From Theorems 8 and 7 it follows that
$k_1k_2(k_1-k_2) \neq 0$. From Theorems 8 and 7 it follows that ![]() $\nu$ is not the zero function. Moreover, the function
$\nu$ is not the zero function. Moreover, the function ![]() $\nu$ is defined on the annulus
$\nu$ is defined on the annulus ![]() $A[1, r)$ with
$A[1, r)$ with ![]() $r \geq c_v^{1/|(k_1,k_2)|_\infty }$, where
$r \geq c_v^{1/|(k_1,k_2)|_\infty }$, where ![]() $c_v = R/|\phi |_v > 1$.
$c_v = R/|\phi |_v > 1$.
We first note that
for a constant ![]() $C_1$ depending only on
$C_1$ depending only on ![]() $\alpha$ and
$\alpha$ and ![]() $v$. Moreover, from Lemma 4.12 it follows that
$v$. Moreover, from Lemma 4.12 it follows that ![]() $-\kappa (\nu,1) \leq |(k_1,k_2)|_\infty \log |\nu |_1/\!\log (|\phi |_v)$. From Lemma 4.6 it follows that
$-\kappa (\nu,1) \leq |(k_1,k_2)|_\infty \log |\nu |_1/\!\log (|\phi |_v)$. From Lemma 4.6 it follows that
and, thus,
As ![]() $|f^{\circ m}(\alpha )|_v = |\Phi (\alpha )|_v^{d^{m}}$ it holds that if
$|f^{\circ m}(\alpha )|_v = |\Phi (\alpha )|_v^{d^{m}}$ it holds that if ![]() $|\Phi (\beta )|_v \geq C_O$ (with
$|\Phi (\beta )|_v \geq C_O$ (with ![]() $C_O$ as in Lemma 4.8), then
$C_O$ as in Lemma 4.8), then ![]() $m$ is bounded and, thus,
$m$ is bounded and, thus, ![]() $h(\beta )$ is also bounded. Thus, there exists a constant
$h(\beta )$ is also bounded. Thus, there exists a constant ![]() $C_4$ depending only on
$C_4$ depending only on ![]() $\alpha, \mathcal {C}$ such that either
$\alpha, \mathcal {C}$ such that either
for positive constants ![]() $C_2,C_3$ depending only on
$C_2,C_3$ depending only on ![]() $\alpha,\mathcal {C}$, or
$\alpha,\mathcal {C}$, or ![]() $h(\beta ) \leq C_4$. We assume from now on that
$h(\beta ) \leq C_4$. We assume from now on that ![]() $h(\beta ) \leq C_4$. If also
$h(\beta ) \leq C_4$. If also ![]() $|(k_1,k_2)|_\infty \leq C_{\text {lower}}$, then it follows from Lemma 4.10 and 4.11 that either
$|(k_1,k_2)|_\infty \leq C_{\text {lower}}$, then it follows from Lemma 4.10 and 4.11 that either
for a constant ![]() $C_6$ depending only on
$C_6$ depending only on ![]() $\alpha, \mathcal {C}$ or
$\alpha, \mathcal {C}$ or ![]() $-\log |\nu |_1 \leq -C_2$. However, if
$-\log |\nu |_1 \leq -C_2$. However, if ![]() $|(k_1,k_2)|_\infty > C_{\text {lower}}$, then it follows from Lemma 4.9 that again the inequality (12) holds. However, from either inequality (13) or (12) it follows that
$|(k_1,k_2)|_\infty > C_{\text {lower}}$, then it follows from Lemma 4.9 that again the inequality (12) holds. However, from either inequality (13) or (12) it follows that
for a constant ![]() $C_7$ depending only on
$C_7$ depending only on ![]() $\alpha, \mathcal {C}$. On the other hand, Lemma 4.7 gives us that
$\alpha, \mathcal {C}$. On the other hand, Lemma 4.7 gives us that
for a constant ![]() $C_8$ depending only on
$C_8$ depending only on ![]() $\alpha, \mathcal {C}$. As
$\alpha, \mathcal {C}$. As ![]() $c <1$, combining the last two inequalities yields
$c <1$, combining the last two inequalities yields ![]() $N \leq C_9$ for
$N \leq C_9$ for ![]() $C_9$ depending only on
$C_9$ depending only on ![]() $\alpha$ and
$\alpha$ and ![]() $\mathcal {C}$. As
$\mathcal {C}$. As ![]() $N\geq 2^{n}$ we obtain a bound on
$N\geq 2^{n}$ we obtain a bound on ![]() $n$.
$n$.
5. Connected Julia sets
In this section we assume that ![]() $f \in \mathbb {C}[X]\setminus \{0\}$ (thus
$f \in \mathbb {C}[X]\setminus \{0\}$ (thus ![]() $\mathcal {K} = \mathbb {C}$) of degree
$\mathcal {K} = \mathbb {C}$) of degree ![]() $d \geq 2$ and that
$d \geq 2$ and that ![]() $f$ is monic. We first recall the following invariants of the dynamical system
$f$ is monic. We first recall the following invariants of the dynamical system
 \begin{align*} B_\infty & = \{z \in \mathbb{C}; |f^{\circ n}(z)| \rightarrow \infty, n\rightarrow \infty \},\\ J & = \{z \in \mathbb{C}; \{f^{\circ n}\}_{n \in \mathbb{Z}_{\geq 0}} \text{ is not a normal family in any neighbourhood of } z\} \end{align*}
\begin{align*} B_\infty & = \{z \in \mathbb{C}; |f^{\circ n}(z)| \rightarrow \infty, n\rightarrow \infty \},\\ J & = \{z \in \mathbb{C}; \{f^{\circ n}\}_{n \in \mathbb{Z}_{\geq 0}} \text{ is not a normal family in any neighbourhood of } z\} \end{align*}
where ![]() $B_\infty$ is called the basin of infinity and
$B_\infty$ is called the basin of infinity and ![]() $J$ is the Julia set of
$J$ is the Julia set of ![]() $f$. These sets are invariants of the dynamical system (hence, equal for all iterates of
$f$. These sets are invariants of the dynamical system (hence, equal for all iterates of ![]() $f$) and for polynomials are related by
$f$) and for polynomials are related by ![]() $\partial B_\infty = J$. In this section, unless we indicate otherwise, we assume that
$\partial B_\infty = J$. In this section, unless we indicate otherwise, we assume that ![]() $J$ is connected. This implies that
$J$ is connected. This implies that ![]() $\Psi$ is meromorphic on a disc of radius 1 [Reference MilnorMil06] and we set
$\Psi$ is meromorphic on a disc of radius 1 [Reference MilnorMil06] and we set
in this section. We moreover have that ![]() $\Psi$ is a bi-holomorphism
$\Psi$ is a bi-holomorphism
(and, thus, is a Riemann mapping of ![]() $B_\infty \cup \{\infty \}$). We make use of real analytic properties of analytic functions so it is convenient to introduce some notation. For any Laurent series
$B_\infty \cup \{\infty \}$). We make use of real analytic properties of analytic functions so it is convenient to introduce some notation. For any Laurent series ![]() $F \in \mathbb {C}((X_1,\ldots, X_n))$ we set
$F \in \mathbb {C}((X_1,\ldots, X_n))$ we set ![]() $F^{h}$ to be the Laurent series obtained by complex conjugating the coefficients of
$F^{h}$ to be the Laurent series obtained by complex conjugating the coefficients of ![]() $F$. For example, if
$F$. For example, if ![]() $F$ is univariate and defines a meromorphic function in some open disc about 0, then
$F$ is univariate and defines a meromorphic function in some open disc about 0, then ![]() $F^{h}(z) = \overline {F(\bar {z})}$ is the usual Schwarz reflection (with
$F^{h}(z) = \overline {F(\bar {z})}$ is the usual Schwarz reflection (with ![]() $\bar {\cdot }$ denoting complex conjugation). In what follows, we define for real
$\bar {\cdot }$ denoting complex conjugation). In what follows, we define for real ![]() $s \leq 1, S^{s} = \{z \in \mathbb {C}; |z|= s\}$. It is straightforward to see that for
$s \leq 1, S^{s} = \{z \in \mathbb {C}; |z|= s\}$. It is straightforward to see that for ![]() $r>0$
$r>0$
In this section we consider an irreducible polynomial ![]() $P \in \mathbb {C}[X,Y]\setminus \{0\}$ defining the curve
$P \in \mathbb {C}[X,Y]\setminus \{0\}$ defining the curve ![]() $\mathcal {C}$. We assume that
$\mathcal {C}$. We assume that ![]() $\partial _XP\partial _YP \neq 0$. Moreover, we assume that
$\partial _XP\partial _YP \neq 0$. Moreover, we assume that ![]() $\mathcal {C}$ has infinite intersection with
$\mathcal {C}$ has infinite intersection with ![]() $L_r^{2}$ for some
$L_r^{2}$ for some ![]() $r > 0$ and we let
$r > 0$ and we let ![]() $\phi = \exp (-r)$. As
$\phi = \exp (-r)$. As ![]() $L_r, \mathcal {C}$ are real analytic sets we deduce that
$L_r, \mathcal {C}$ are real analytic sets we deduce that ![]() $\mathcal {C}\cap L_r^{2}$ contains an analytic connected arc. Thus, we obtain an analytic curve
$\mathcal {C}\cap L_r^{2}$ contains an analytic connected arc. Thus, we obtain an analytic curve ![]() $(a_1,a_2):(0,1) \rightarrow (S^{1})^{2}$ such that
$(a_1,a_2):(0,1) \rightarrow (S^{1})^{2}$ such that
As ![]() $a_1^{h} = 1/a_1, a_2^{h} = 1/a_2$ we obtain that there is an analytic arc
$a_1^{h} = 1/a_1, a_2^{h} = 1/a_2$ we obtain that there is an analytic arc ![]() $\mathcal {A}\subset S^{\phi }\times S^{\phi }$ such that
$\mathcal {A}\subset S^{\phi }\times S^{\phi }$ such that
As our proofs rely on analytic continuation we are going to use paths frequently. For a path ![]() $\gamma : I \rightarrow X$ into some complex analytic set
$\gamma : I \rightarrow X$ into some complex analytic set ![]() $X$ we denote by
$X$ we denote by ![]() $|\gamma |$ its support
$|\gamma |$ its support ![]() $\gamma (I)$. Here
$\gamma (I)$. Here ![]() $I$ is an interval (not necessarily open or closed) and we always assume that
$I$ is an interval (not necessarily open or closed) and we always assume that ![]() $\gamma$ is piecewise smooth. For a set
$\gamma$ is piecewise smooth. For a set ![]() $U \subset \mathbb {C}$ we denote by
$U \subset \mathbb {C}$ we denote by ![]() $\partial U, \bar {U}$ its boundary and closure, respectively. Further, we denote by
$\partial U, \bar {U}$ its boundary and closure, respectively. Further, we denote by ![]() $U^{h}$ its complex conjugate.
$U^{h}$ its complex conjugate.
We give a brief summary of the proof strategy in this section. Our proof proceeds by constructing a pseudo-involution ![]() $\mu$ on the set
$\mu$ on the set
By a pseudo-involution we mean an analytic map ![]() $i:\mathcal {F} \rightarrow \mathcal {F}^{h}$ such that
$i:\mathcal {F} \rightarrow \mathcal {F}^{h}$ such that ![]() $i\circ i^{h} = \text {id}$. Using (14) we show that
$i\circ i^{h} = \text {id}$. Using (14) we show that ![]() $\mathcal {C}$ intersects
$\mathcal {C}$ intersects ![]() $\partial \mathcal {F}^{2}$ in a relatively open subset unless
$\partial \mathcal {F}^{2}$ in a relatively open subset unless ![]() $f$ is exceptional. More specifically, because
$f$ is exceptional. More specifically, because ![]() $\partial \mathcal {F} = \Psi (S^{\phi ^{2}})\times J$, we show then that either the smooth boundary component
$\partial \mathcal {F} = \Psi (S^{\phi ^{2}})\times J$, we show then that either the smooth boundary component ![]() $\Psi (S^{\phi ^{2}})$ parameterises a relatively open subset of
$\Psi (S^{\phi ^{2}})$ parameterises a relatively open subset of ![]() $J$ which implies again that
$J$ which implies again that ![]() $f$ is exceptional or
$f$ is exceptional or ![]() $\mathcal {C}$ intersects
$\mathcal {C}$ intersects ![]() $\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}})$ in infinitely many points. We can then proceed inductively to construct infinitely many pseudo-involutions. This construction allows us to use Schwarz's lemma to show that the polynomial
$\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}})$ in infinitely many points. We can then proceed inductively to construct infinitely many pseudo-involutions. This construction allows us to use Schwarz's lemma to show that the polynomial ![]() $P$ defines a ‘rotation’ of
$P$ defines a ‘rotation’ of ![]() $B_\infty$. We then use a theorem of Levin to show that this rotation is, in fact, rational. However, in order to show that this rotation defines a curve as defined in Theorem 3 we also need to employ the classification of periodic curves by Medvedev and Scanlon.
$B_\infty$. We then use a theorem of Levin to show that this rotation is, in fact, rational. However, in order to show that this rotation defines a curve as defined in Theorem 3 we also need to employ the classification of periodic curves by Medvedev and Scanlon.
Our starting point for a proof of Theorem 3 is an observation on complex algebraic curves.
Lemma 5.1 Let ![]() $U_1,U_2 \subset \mathbb {C}$ be bounded open and connected. Let
$U_1,U_2 \subset \mathbb {C}$ be bounded open and connected. Let ![]() $C$ be an irreducible complex plane curve whose projection to each coordinate is a dominant map. We denote the canonical projections to the affine coordinates
$C$ be an irreducible complex plane curve whose projection to each coordinate is a dominant map. We denote the canonical projections to the affine coordinates ![]() $\pi _1,\pi _2$. Suppose that
$\pi _1,\pi _2$. Suppose that ![]() $C(\mathbb {C}) \cap U_1\times U_2$ is non-empty. If
$C(\mathbb {C}) \cap U_1\times U_2$ is non-empty. If ![]() $C(\mathbb {C})\cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is empty, then each path
$C(\mathbb {C})\cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is empty, then each path ![]() $|\gamma | \subset U_1$ or
$|\gamma | \subset U_1$ or ![]() $|\gamma | \subset U_2$ can be lifted to a path in
$|\gamma | \subset U_2$ can be lifted to a path in ![]() $C\cap U_1\times U_2$ (via
$C\cap U_1\times U_2$ (via ![]() $\pi _1$ or
$\pi _1$ or ![]() $\pi _2$, respectively). Moreover, the maps
$\pi _2$, respectively). Moreover, the maps ![]() $\pi _i :C \cap \overline {U_1}\times \overline {U_2} \rightarrow \bar {U}_i, i = 1,2$, are surjective and
$\pi _i :C \cap \overline {U_1}\times \overline {U_2} \rightarrow \bar {U}_i, i = 1,2$, are surjective and ![]() $\pi _1^{-1}(\partial U_1) = \pi _2^{-1}(\partial U_2) \subset \partial U_1 \times \partial U_2$.
$\pi _1^{-1}(\partial U_1) = \pi _2^{-1}(\partial U_2) \subset \partial U_1 \times \partial U_2$.
If the boundaries ![]() $\partial U_1, \partial U_2$ do not contain isolated points and
$\partial U_1, \partial U_2$ do not contain isolated points and ![]() $C \cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is non-empty then, it contains infinitely many points.
$C \cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is non-empty then, it contains infinitely many points.
Proof. For the first part of the statement, assume that ![]() $C \cap U_1\times U_2$ is non-empty and let
$C \cap U_1\times U_2$ is non-empty and let ![]() $\gamma :[0,1]\rightarrow U_1$ be a path such that
$\gamma :[0,1]\rightarrow U_1$ be a path such that ![]() $\gamma (0) \in \pi _1(C\cap U_1\times U_2)$. As
$\gamma (0) \in \pi _1(C\cap U_1\times U_2)$. As ![]() $C$ is connected we can lift
$C$ is connected we can lift ![]() $\gamma$ to a path
$\gamma$ to a path ![]() $\tilde {\gamma }:[0,1] \rightarrow C$ such that
$\tilde {\gamma }:[0,1] \rightarrow C$ such that ![]() $\pi _2(\tilde {\gamma }(0)) \in U_2$ and as
$\pi _2(\tilde {\gamma }(0)) \in U_2$ and as ![]() $C\cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is empty,
$C\cap (\partial U_1\times U_2\cup U_1\times \partial U_2)$ is empty, ![]() $|\pi _2\circ \tilde {\gamma } | \subset U_2$ by the intermediate value theorem. We can repeat the arguments for a path in
$|\pi _2\circ \tilde {\gamma } | \subset U_2$ by the intermediate value theorem. We can repeat the arguments for a path in ![]() $U_2$ and obtain the first part of the statement. As
$U_2$ and obtain the first part of the statement. As ![]() $U_1$ is path connected we can find for each boundary point of
$U_1$ is path connected we can find for each boundary point of ![]() $U_1$ a path
$U_1$ a path ![]() $\gamma$ as previously with the endpoint being that boundary point. This proves that
$\gamma$ as previously with the endpoint being that boundary point. This proves that ![]() $\pi _1, \pi _2$ surject onto the boundaries.
$\pi _1, \pi _2$ surject onto the boundaries.
If ![]() $(x_0,y_0) \in C \cap \partial U_1\times U_2$, then as
$(x_0,y_0) \in C \cap \partial U_1\times U_2$, then as ![]() $\partial U_1$ does not contain isolated points, each neighbourhood of
$\partial U_1$ does not contain isolated points, each neighbourhood of ![]() $x_0$ contains infinitely many points of
$x_0$ contains infinitely many points of ![]() $\partial U_1$. Employing the implicit function theorem or Puiseux's theorem, we can find a non-constant analytic function
$\partial U_1$. Employing the implicit function theorem or Puiseux's theorem, we can find a non-constant analytic function ![]() $h$ defined on a neighbourhood of 0 and satisfying
$h$ defined on a neighbourhood of 0 and satisfying ![]() $h(0) = x_0$ and a positive integer
$h(0) = x_0$ and a positive integer ![]() $N$ such that
$N$ such that ![]() $(h(x), y_0 + x^{N}) \in C(\mathbb {C})$ for
$(h(x), y_0 + x^{N}) \in C(\mathbb {C})$ for ![]() $x$. We can find infinitely many
$x$. We can find infinitely many ![]() $x$ in any neighbourhood of
$x$ in any neighbourhood of ![]() $0$ such that
$0$ such that ![]() $y_0 + x^{N} \in \partial U_1$ and
$y_0 + x^{N} \in \partial U_1$ and ![]() $h(x) \in U_1$. This proves the claim.
$h(x) \in U_1$. This proves the claim.
We define an analytic function ![]() $\mu$ on
$\mu$ on ![]() $\mathcal {F}$ by
$\mathcal {F}$ by
and we call ![]() $\mu$ a pseudo-involution as
$\mu$ a pseudo-involution as ![]() $\mu :\mathcal {F} \rightarrow \mathcal {F}^{h}$ is bijective with
$\mu :\mathcal {F} \rightarrow \mathcal {F}^{h}$ is bijective with ![]() $\mu ^{h}\circ \mu = \mu \circ \mu ^{h} = \text {id}$. We can reformulate the relations (14) in terms of
$\mu ^{h}\circ \mu = \mu \circ \mu ^{h} = \text {id}$. We can reformulate the relations (14) in terms of ![]() $\mu$ as
$\mu$ as
where ![]() $\mathcal {B} = \Psi (\mathcal {A})$. We also note that
$\mathcal {B} = \Psi (\mathcal {A})$. We also note that ![]() $J(f^{h}) = J^{h},\ B_\infty (f^{h}) = B_\infty ^{h}$.
$J(f^{h}) = J^{h},\ B_\infty (f^{h}) = B_\infty ^{h}$.
Lemma 5.2 The function ![]() $\mu$ has the property that for each sequence
$\mu$ has the property that for each sequence ![]() $\{x_n\}_{n} \subset F$ such that
$\{x_n\}_{n} \subset F$ such that ![]() $\lim _n x_n = x \in J$ it holds that every limit point
$\lim _n x_n = x \in J$ it holds that every limit point ![]() $y$ of
$y$ of ![]() $\{\mu (x_n)\}$ satisfies
$\{\mu (x_n)\}$ satisfies ![]() $y \in \Psi ^{h}(S^{\phi ^{2}})$. Similarly, for each
$y \in \Psi ^{h}(S^{\phi ^{2}})$. Similarly, for each ![]() $\{x_n\}_n \subset F$ such that
$\{x_n\}_n \subset F$ such that ![]() $\lim _nx_n = x \in \Psi (S^{\phi ^{2}})$ any limit point
$\lim _nx_n = x \in \Psi (S^{\phi ^{2}})$ any limit point ![]() $y$ of
$y$ of ![]() $\{ \mu (x_n)\}_n$ satisfies
$\{ \mu (x_n)\}_n$ satisfies ![]() $y \in J^{h}$.
$y \in J^{h}$.
Proof. This follows from the fact that ![]() $J$ is the boundary of
$J$ is the boundary of ![]() $B_\infty$ and that
$B_\infty$ and that ![]() $B_\infty = \Psi (D^{*})$.
$B_\infty = \Psi (D^{*})$.
We use the properties of ![]() $\mu$ that are outlined in Lemma 5.2 to deduce that the existence of such an arc
$\mu$ that are outlined in Lemma 5.2 to deduce that the existence of such an arc ![]() $\mathcal {B}$ (15) implies that
$\mathcal {B}$ (15) implies that ![]() $f$ has to be exceptional. Our strategy is to reduce this to the following theorem of Fatou that he proved in his seminal papers.
$f$ has to be exceptional. Our strategy is to reduce this to the following theorem of Fatou that he proved in his seminal papers.
Theorem 9 [Reference FatouFat20, p. 250]
If a relatively open subset of the Julia set of a rational map ![]() $f$ is an analytic arc, then
$f$ is an analytic arc, then ![]() $f$ is conjugate to an exceptional polynomial.
$f$ is conjugate to an exceptional polynomial.
By an analytic arc we mean the image of an analytic map ![]() $\gamma :(0,1) \rightarrow \mathbb {C}$. We recall that
$\gamma :(0,1) \rightarrow \mathbb {C}$. We recall that ![]() $P$ is the polynomial defining
$P$ is the polynomial defining ![]() $\mathcal {C}$ and we set
$\mathcal {C}$ and we set ![]() $C_0$ to be the connected component of
$C_0$ to be the connected component of ![]() $\mathcal {C} \cap \mathcal {F}^{2}$ containing
$\mathcal {C} \cap \mathcal {F}^{2}$ containing ![]() $\mathcal {B}$.
$\mathcal {B}$.
Lemma 5.3 Suppose there exists ![]() $(x_0,y_0) \in \overline {C_0}\cap ( \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ such that
$(x_0,y_0) \in \overline {C_0}\cap ( \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ such that ![]() $P(x_0,y_0) = 0$. Then we can continue
$P(x_0,y_0) = 0$. Then we can continue ![]() $\mu$ analytically to an open disc centred at a point
$\mu$ analytically to an open disc centred at a point ![]() $x \in \Psi (S^{\phi ^{2}})$.
$x \in \Psi (S^{\phi ^{2}})$.
Proof. We can assume that ![]() $(x_0,y_0) \in \partial \mathcal {F} \times \mathcal {F}$ and from the relation (15) as well as Lemma 5.2 follows that we may assume that
$(x_0,y_0) \in \partial \mathcal {F} \times \mathcal {F}$ and from the relation (15) as well as Lemma 5.2 follows that we may assume that ![]() $(x_0,y_0) \in \Psi (S^{\phi ^{2}})\times \mathcal {F}$ (up to replacing
$(x_0,y_0) \in \Psi (S^{\phi ^{2}})\times \mathcal {F}$ (up to replacing ![]() $P$ by
$P$ by ![]() $P^{h}$ and
$P^{h}$ and ![]() $C_0$ by
$C_0$ by ![]() $(\mu, \mu )(C_0)$. As
$(\mu, \mu )(C_0)$. As ![]() $\partial \mathcal {F}$ does not contain isolated points we can pick
$\partial \mathcal {F}$ does not contain isolated points we can pick ![]() $(x_0,y_0)$ such that
$(x_0,y_0)$ such that ![]() $\partial _Y P(x_0,y_0)\partial _Y P(x,\mu (y_0)) \neq 0$ for all
$\partial _Y P(x_0,y_0)\partial _Y P(x,\mu (y_0)) \neq 0$ for all ![]() $x$ such that
$x$ such that ![]() $P(x,\mu (y_0))= 0$. We can pick an open disc
$P(x,\mu (y_0))= 0$. We can pick an open disc ![]() $D$ centred at
$D$ centred at ![]() $x_0$ such that
$x_0$ such that ![]() $D \setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with
$D \setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with ![]() $D_1, D_2$ open and such that
$D_1, D_2$ open and such that ![]() ${D_1 \subset \mathcal {F}, D_2 \subset \mathbb {C}\setminus \mathcal {F}}$. Moreover, such that there exists an analytic function
${D_1 \subset \mathcal {F}, D_2 \subset \mathbb {C}\setminus \mathcal {F}}$. Moreover, such that there exists an analytic function ![]() $h$ on
$h$ on ![]() $D$ with
$D$ with ![]() $h(x_0) = y_0$ and
$h(x_0) = y_0$ and ![]() $P(x,h(x)) = 0$ for
$P(x,h(x)) = 0$ for ![]() $x \in D$. We then have that
$x \in D$. We then have that
As ![]() $y_0 \in \mathcal {F}$,
$y_0 \in \mathcal {F}$, ![]() $\mu (y_0) = \mu \circ h(x_0) \in \mathcal {F}$. We set
$\mu (y_0) = \mu \circ h(x_0) \in \mathcal {F}$. We set ![]() $\mu (x_0)$ to be equal to a limit of points
$\mu (x_0)$ to be equal to a limit of points ![]() $\mu (x_n)$ where
$\mu (x_n)$ where ![]() $(x_n)_n$ is a sequence of points in
$(x_n)_n$ is a sequence of points in ![]() $D_1$ converging to
$D_1$ converging to ![]() $x_0$. As
$x_0$. As ![]() $\partial _YP(x,\mu (y_0))\neq 0$ for all
$\partial _YP(x,\mu (y_0))\neq 0$ for all ![]() $x$ satisfying
$x$ satisfying ![]() $P(x,y) = 0$ there exists an analytic function
$P(x,y) = 0$ there exists an analytic function ![]() $\tilde {h}$ on an open disc
$\tilde {h}$ on an open disc ![]() $\tilde {D}$ centred at
$\tilde {D}$ centred at ![]() $\mu (y_0)$ satisfying
$\mu (y_0)$ satisfying ![]() $P(\tilde {h}(y), y) = 0$ for all
$P(\tilde {h}(y), y) = 0$ for all ![]() $y \in \tilde {D}$ and
$y \in \tilde {D}$ and ![]() $\tilde {h}(\mu (y_0)) = \mu (x_0)$. We can shrink
$\tilde {h}(\mu (y_0)) = \mu (x_0)$. We can shrink ![]() $D$ such that
$D$ such that ![]() $\mu \circ h(D)\subset \tilde {D}$. From the uniqueness of
$\mu \circ h(D)\subset \tilde {D}$. From the uniqueness of ![]() $\tilde {h}$ it follows that
$\tilde {h}$ it follows that
for all ![]() $x \in D_1$ and so
$x \in D_1$ and so ![]() $\tilde {h}\circ \mu \circ h(x)$ is a continuation of
$\tilde {h}\circ \mu \circ h(x)$ is a continuation of ![]() $\mu$ to
$\mu$ to ![]() $D$.
$D$.
Lemma 5.4 Suppose we can continue ![]() $\mu$ analytically to an open disc centred at
$\mu$ analytically to an open disc centred at ![]() $\Psi (S^{\phi ^{2}})$. Then we can find a small disc
$\Psi (S^{\phi ^{2}})$. Then we can find a small disc ![]() $D$ centred at
$D$ centred at ![]() $x_0 \in \Psi (S^{\phi ^{2}})$ with the following properties. It holds that
$x_0 \in \Psi (S^{\phi ^{2}})$ with the following properties. It holds that ![]() $D\setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with
$D\setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with ![]() $D_1,D_2$ open such that
$D_1,D_2$ open such that ![]() $D_1 \subset \mathcal {F}, D_2 \subset \Psi (A(0,\phi ^{2}))$. Moreover,
$D_1 \subset \mathcal {F}, D_2 \subset \Psi (A(0,\phi ^{2}))$. Moreover, ![]() $\mu$ continues to
$\mu$ continues to ![]() $D$ and
$D$ and ![]() $\mu ^{h}$ to
$\mu ^{h}$ to ![]() $\mu (D)$ and it holds that
$\mu (D)$ and it holds that ![]() $\mu ^{h}\circ \mu (z) = z$ on
$\mu ^{h}\circ \mu (z) = z$ on ![]() $\mathcal {F}\cup D$.
$\mathcal {F}\cup D$.
Proof. The first part of the lemma concerning the choice of ![]() $D$ follows from the fact that
$D$ follows from the fact that ![]() $\Psi (S^{\phi ^{2}})$ is an analytic arc we can further choose
$\Psi (S^{\phi ^{2}})$ is an analytic arc we can further choose ![]() $D$ such that
$D$ such that ![]() $\mu '(z) \neq 0$ on
$\mu '(z) \neq 0$ on ![]() $D$ and
$D$ and ![]() $\mu (D)$ is simply connected. Thus, we can define
$\mu (D)$ is simply connected. Thus, we can define ![]() $\mu ^{-1}$ on
$\mu ^{-1}$ on ![]() $\mu (D)$ and as it holds that
$\mu (D)$ and as it holds that
we can continue ![]() $\mu ^{h}$ to
$\mu ^{h}$ to ![]() $\mu (D)$ and so it holds that
$\mu (D)$ and so it holds that ![]() $\mu ^{h}\circ \mu (z) = z$ on
$\mu ^{h}\circ \mu (z) = z$ on ![]() $\mathcal {F}\cup D$.
$\mathcal {F}\cup D$.
Corollary 5.5 Suppose we can continue ![]() $\mu$ analytically to a disc
$\mu$ analytically to a disc ![]() $D$ centred at
$D$ centred at ![]() $x_0 \in \Psi (S^{\phi ^{2}})$. Then
$x_0 \in \Psi (S^{\phi ^{2}})$. Then ![]() $f$ is exceptional.
$f$ is exceptional.
Proof. We can assume that ![]() $D$ is as in the previous lemma and we set
$D$ is as in the previous lemma and we set ![]() $D_1, D_2$ as in the previous lemma. We first note that
$D_1, D_2$ as in the previous lemma. We first note that ![]() $\mu$ is injective on
$\mu$ is injective on ![]() $\mathcal {F} \cup D$ as it has a global inverse. Thus,
$\mathcal {F} \cup D$ as it has a global inverse. Thus, ![]() $\mu (D_1) \subset \mathcal {F}^{h}$ and
$\mu (D_1) \subset \mathcal {F}^{h}$ and ![]() $\mu (D_2) \subset \mathbb {C}\setminus B_\infty ^{h}$ as
$\mu (D_2) \subset \mathbb {C}\setminus B_\infty ^{h}$ as ![]() $\mu (\mathcal {F}) = \mathcal {F}^{h}$ and
$\mu (\mathcal {F}) = \mathcal {F}^{h}$ and ![]() $\mu$ is injective. It follows that
$\mu$ is injective. It follows that ![]() $\mu (\Psi (S^{\phi ^{2}})\cap D) = J^{h}\cap \mu (D)$ and the claim follows from Fatou's theorem (Theorem 9).
$\mu (\Psi (S^{\phi ^{2}})\cap D) = J^{h}\cap \mu (D)$ and the claim follows from Fatou's theorem (Theorem 9).
We turn to the case for which ![]() $\overline {C_0} \cap \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ is empty. With the following lemma we discard one case right away.
$\overline {C_0} \cap \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ is empty. With the following lemma we discard one case right away.
Lemma 5.6 Suppose that ![]() $\overline {C_0} \cap \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ as well as
$\overline {C_0} \cap \partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ as well as ![]() $\overline {C_0}\cap ( \Psi (S^{\phi ^{2}})^{2}\cup J^{2})$ is empty. Then
$\overline {C_0}\cap ( \Psi (S^{\phi ^{2}})^{2}\cup J^{2})$ is empty. Then ![]() $f$ is exceptional.
$f$ is exceptional.
Proof. By Lemma 5.1 it holds that the projections ![]() $\pi _1, \pi _2$ from
$\pi _1, \pi _2$ from ![]() $\overline {C_0} \cap \bar {\mathcal {F}}^{2}$ to
$\overline {C_0} \cap \bar {\mathcal {F}}^{2}$ to ![]() $\partial \mathcal {F}$ are surjective. As
$\partial \mathcal {F}$ are surjective. As ![]() $\partial \mathcal {F} = \Psi (S^{\phi ^{2}})\times J\cup J \times \Psi (S^{\phi ^{2}})$ and our assumption it holds that
$\partial \mathcal {F} = \Psi (S^{\phi ^{2}})\times J\cup J \times \Psi (S^{\phi ^{2}})$ and our assumption it holds that ![]() $\pi _2(\pi _{1}^{-1}(\Psi (S^{\phi ^{2}}))) = J$. This implies that
$\pi _2(\pi _{1}^{-1}(\Psi (S^{\phi ^{2}}))) = J$. This implies that ![]() $J$ is a finite union of points and analytic arcs.
$J$ is a finite union of points and analytic arcs.
However, we can construct a smooth open subset of ![]() $J$ concretely. For this fix
$J$ concretely. For this fix ![]() $y_0 \in J$ such that
$y_0 \in J$ such that ![]() $\partial P(x,y_0)\partial _Y P(x,y_0)\neq 0$ for all
$\partial P(x,y_0)\partial _Y P(x,y_0)\neq 0$ for all ![]() $(x,y_0)\in \mathbb {C}^{2}$ satisfying
$(x,y_0)\in \mathbb {C}^{2}$ satisfying ![]() $P(x,y_0) = 0$.
$P(x,y_0) = 0$.
Let ![]() $D$ be an open disc in a neighbourhood of
$D$ be an open disc in a neighbourhood of ![]() $y$ such that there exists
$y$ such that there exists ![]() $n$, open connected sets
$n$, open connected sets ![]() $U_1, \ldots,U_n$ and analytic functions
$U_1, \ldots,U_n$ and analytic functions ![]() $h_i$ on
$h_i$ on ![]() $U_i, i = 1, \ldots,n$ such that
$U_i, i = 1, \ldots,n$ such that
It holds that ![]() $h_i(U_i \cap \Psi (S^{\phi ^{2}})) \cap h_j(U_{j} \cap \Psi (S^{\phi ^{2}}))$ is a finite union of points and analytic arcs for
$h_i(U_i \cap \Psi (S^{\phi ^{2}})) \cap h_j(U_{j} \cap \Psi (S^{\phi ^{2}}))$ is a finite union of points and analytic arcs for ![]() $i,j \in \{1, \ldots, n\}$. Thus, we can find a point
$i,j \in \{1, \ldots, n\}$. Thus, we can find a point ![]() $y_1 \in D \cap J$ and an open neighbourhood
$y_1 \in D \cap J$ and an open neighbourhood ![]() $U$ of
$U$ of ![]() $y_1$ such that
$y_1$ such that ![]() $U \cap J$ is an analytic arc. The lemma now follows from Fatou's theorem.
$U \cap J$ is an analytic arc. The lemma now follows from Fatou's theorem.
Before we proceed, we record a lemma that is a more or less straightforward consequence of Schwarz's lemma.
Lemma 5.7 Let ![]() $\mathcal {G}$ be an analytic non-zero function in two variables on
$\mathcal {G}$ be an analytic non-zero function in two variables on ![]() $D^{2}$. Suppose that there exists a sequence of circles
$D^{2}$. Suppose that there exists a sequence of circles ![]() $S_n$ whose radius
$S_n$ whose radius ![]() $r_n$ tends to zero as
$r_n$ tends to zero as ![]() $n$ tends to infinity such that for all
$n$ tends to infinity such that for all ![]() $n \in \mathbb {Z}_{\geq 0}$,
$n \in \mathbb {Z}_{\geq 0}$, ![]() $\mathcal {G}(x,y) = 0$ for infinitely many
$\mathcal {G}(x,y) = 0$ for infinitely many ![]() $(x,y) \in S_n^{2}$. Then there exists a complex number
$(x,y) \in S_n^{2}$. Then there exists a complex number ![]() $\theta \in S^{1}$ such that
$\theta \in S^{1}$ such that ![]() $\mathcal {G}(x,\theta x) =0$ identically.
$\mathcal {G}(x,\theta x) =0$ identically.
Proof. First, by continuity, ![]() $\mathcal {G}(0,0) = 0$. We may assume that
$\mathcal {G}(0,0) = 0$. We may assume that ![]() $\mathcal {G}$ is irreducible [Reference ZoladekZol06] and then by Puiseux's theorem as given in Lemma 6.2 there exists an analytic function
$\mathcal {G}$ is irreducible [Reference ZoladekZol06] and then by Puiseux's theorem as given in Lemma 6.2 there exists an analytic function ![]() $h$ in a neighbourhood
$h$ in a neighbourhood ![]() $U_0$ of 0 and a positive integer
$U_0$ of 0 and a positive integer ![]() $N$ such that
$N$ such that ![]() $(x^{N}, h(x))$,
$(x^{N}, h(x))$, ![]() $x \in U_0$ parameterises a neighbourhood of 0 of the zero set of
$x \in U_0$ parameterises a neighbourhood of 0 of the zero set of ![]() $\mathcal {G}$. For
$\mathcal {G}$. For ![]() $n$ large enough
$n$ large enough ![]() $S_n$ is contained in
$S_n$ is contained in ![]() $U_0$ and we may renumber
$U_0$ and we may renumber ![]() $S_n$ such that all of them are. We have that for each
$S_n$ such that all of them are. We have that for each ![]() $n \geq 0$ there are infinitely many
$n \geq 0$ there are infinitely many ![]() $x_n \in \mathbb {C}$ with
$x_n \in \mathbb {C}$ with ![]() $|x_n| = r_n^{1/N}$ and for which
$|x_n| = r_n^{1/N}$ and for which
holds. By analytic continuation this then holds for all ![]() $x$ of absolute value
$x$ of absolute value ![]() $r_n^{1/N}$. Thus, writing
$r_n^{1/N}$. Thus, writing ![]() $h$ in polar coordinates
$h$ in polar coordinates ![]() $(r,\omega )$ we have
$(r,\omega )$ we have ![]() $\partial _\omega h(r_0,\omega _0) = 0$ for all
$\partial _\omega h(r_0,\omega _0) = 0$ for all ![]() $(r_0,\omega ) \in \{r_n, n \in \mathbb {Z}_{\geq 0}\}\times [0,2\pi )$ and we deduce that
$(r_0,\omega ) \in \{r_n, n \in \mathbb {Z}_{\geq 0}\}\times [0,2\pi )$ and we deduce that ![]() $\partial _\omega |h(r,\omega )| = 0$ identically. We also have
$\partial _\omega |h(r,\omega )| = 0$ identically. We also have ![]() $|h(r,\omega )| = |h(r)| = r^{N}$ for infinitely
$|h(r,\omega )| = |h(r)| = r^{N}$ for infinitely ![]() $r$ and so
$r$ and so ![]() $|h(r)| = r^{N}$ identically by analyticity. However, this also implies that
$|h(r)| = r^{N}$ identically by analyticity. However, this also implies that ![]() $h(z) = z^{N}(1 + O(z))$ and so
$h(z) = z^{N}(1 + O(z))$ and so ![]() $h = \tilde {h}^{N}$ for an analytic function
$h = \tilde {h}^{N}$ for an analytic function ![]() $\tilde {h}(z)$ satisfying
$\tilde {h}(z)$ satisfying ![]() $\tilde {h}(0) = 0$. This contradicts irreducibility if
$\tilde {h}(0) = 0$. This contradicts irreducibility if ![]() $N \geq 2$ and we deduce that
$N \geq 2$ and we deduce that ![]() $|h(z)| = |z|$. By Schwarz's Lemma
$|h(z)| = |z|$. By Schwarz's Lemma ![]() $h(z) = \theta z$ for some
$h(z) = \theta z$ for some ![]() $\theta \in S^{1}$.
$\theta \in S^{1}$.
Now we come to the final proposition of this subsection.
Proposition 5.8 Suppose that ![]() $f$ is not exceptional and let
$f$ is not exceptional and let ![]() $P, \mathcal {B}$ be as in (15). There exists
$P, \mathcal {B}$ be as in (15). There exists ![]() $\theta \in S^{1}$ such that
$\theta \in S^{1}$ such that
identically.
Proof. By Lemma 5.3 and Corollary 5.5 and our assumption on ![]() $f$ to be non-exceptional we may assume that
$f$ to be non-exceptional we may assume that ![]() $\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty. By Lemmas 5.6 and 5.2 it holds that
$\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty. By Lemmas 5.6 and 5.2 it holds that ![]() $\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ or
$\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ or ![]() $\overline {C_0^{h}} \cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty. We first assume that the former holds. As
$\overline {C_0^{h}} \cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty. We first assume that the former holds. As ![]() $\Psi (S^{\phi ^{2}})$ is connected and
$\Psi (S^{\phi ^{2}})$ is connected and ![]() $\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty we can find infinitely many points in
$\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty we can find infinitely many points in ![]() $\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ and, thus, an analytic arc
$\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ and, thus, an analytic arc ![]() $\mathcal {B}_1$ in
$\mathcal {B}_1$ in ![]() $\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$. If
$\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$. If ![]() $\bar {C}^{h}_0 \cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty we can use the same arguments to prove that this contains an analytic arc. However, complex conjugating the arc we see that then also
$\bar {C}^{h}_0 \cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty we can use the same arguments to prove that this contains an analytic arc. However, complex conjugating the arc we see that then also ![]() $\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ contains an analytic arc.
$\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ contains an analytic arc.
We can repeat all of the above arguments with ![]() $\phi$ replaced by
$\phi$ replaced by ![]() $\phi ^{2}$ to deduce that there is an analytic arc in
$\phi ^{2}$ to deduce that there is an analytic arc in ![]() $\mathcal {C}\cap \Psi (S^{\phi ^{4}})\times \Psi (S^{\phi ^{4}})$. We can continue inductively and deduce that
$\mathcal {C}\cap \Psi (S^{\phi ^{4}})\times \Psi (S^{\phi ^{4}})$. We can continue inductively and deduce that ![]() $\mathcal {C} \cap \Psi (S^{\phi ^{2^{N}}}\!)\times \Psi (S^{\phi ^{2^{N}}}\!)$ contains a (connected) analytic arc
$\mathcal {C} \cap \Psi (S^{\phi ^{2^{N}}}\!)\times \Psi (S^{\phi ^{2^{N}}}\!)$ contains a (connected) analytic arc ![]() $\mathcal {B}_N$ for all integers
$\mathcal {B}_N$ for all integers ![]() $N \geq 0$. Thus, setting
$N \geq 0$. Thus, setting ![]() $\mathcal {G}(x,y) = x^{\deg _X P}y^{\deg _YP}P(\Psi (x), \Psi (y))$ in Lemma 5.7 we finish the proof.
$\mathcal {G}(x,y) = x^{\deg _X P}y^{\deg _YP}P(\Psi (x), \Psi (y))$ in Lemma 5.7 we finish the proof.
5.1 Rotations of the basin of infinity
In this subsection we prove the following lemma.
Lemma 5.9 Suppose that ![]() $f$ is not an exceptional polynomial with connected Julia set and suppose that there exists an irreducible polynomial
$f$ is not an exceptional polynomial with connected Julia set and suppose that there exists an irreducible polynomial ![]() $P \in \mathbb {C}[X,Y]\setminus \{0\}$ and a complex number
$P \in \mathbb {C}[X,Y]\setminus \{0\}$ and a complex number ![]() $\theta$ of absolute value 1 such that
$\theta$ of absolute value 1 such that ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ for all
$P(\Psi (z), \Psi (\theta z)) = 0$ for all ![]() $z \in D$. Then
$z \in D$. Then ![]() $\theta$ is a root of unity.
$\theta$ is a root of unity.
We assume that ![]() $\theta$ is not a root of unity and then construct a non-trivial family of symmetries of the Julia set
$\theta$ is not a root of unity and then construct a non-trivial family of symmetries of the Julia set ![]() $J(f)$ of
$J(f)$ of ![]() $f$ and by a theorem of Levin [Reference LevinLev91, Theorem 1] and Douady and Hubbard [Reference Douady and HubbardDH93] the existence of such a family implies that
$f$ and by a theorem of Levin [Reference LevinLev91, Theorem 1] and Douady and Hubbard [Reference Douady and HubbardDH93] the existence of such a family implies that ![]() $f$ is exceptional.
$f$ is exceptional.
Proof of Lemma 5.9 In what follows, we assume that ![]() $\theta$ is not a root of unity and derive a contradiction. We first note that the partial derivatives of
$\theta$ is not a root of unity and derive a contradiction. We first note that the partial derivatives of ![]() $P$ do not vanish identically. Otherwise
$P$ do not vanish identically. Otherwise ![]() $\Psi$ would be a constant function. We denote by
$\Psi$ would be a constant function. We denote by ![]() $h_\theta$ the function
$h_\theta$ the function
and, by assumption, ![]() $h_\theta$ is an algebraic function that can be continued to some disc centred at a point of
$h_\theta$ is an algebraic function that can be continued to some disc centred at a point of ![]() $J(f)$. Thus, we can continue
$J(f)$. Thus, we can continue ![]() $h_\theta$ as an analytic function to an open disc
$h_\theta$ as an analytic function to an open disc ![]() $D$ centred at
$D$ centred at ![]() $x_0\in J$. Choosing
$x_0\in J$. Choosing ![]() $D$ small enough
$D$ small enough ![]() $h_\theta$ is bi-holomorphic onto its image. Clearly
$h_\theta$ is bi-holomorphic onto its image. Clearly ![]() $h_\theta (D) \cap B_\infty$ is open and non-empty and, hence, we can continue
$h_\theta (D) \cap B_\infty$ is open and non-empty and, hence, we can continue ![]() $h_{\theta ^{-1}}$ to
$h_{\theta ^{-1}}$ to ![]() $h_\theta (D)$ using the relation
$h_\theta (D)$ using the relation ![]() $h_\theta ^{-1}(z) = h_{\theta ^{-1}}(z)$ for
$h_\theta ^{-1}(z) = h_{\theta ^{-1}}(z)$ for ![]() $z \in h_\theta (D) \cap B_\infty$. It follows that
$z \in h_\theta (D) \cap B_\infty$. It follows that ![]() $h_\theta (D \cap \mathbb {C}\setminus B_\infty ) \subset \mathbb {C}\setminus B_\infty$ because
$h_\theta (D \cap \mathbb {C}\setminus B_\infty ) \subset \mathbb {C}\setminus B_\infty$ because ![]() $h_{\theta ^{-1}}(B_\infty ) = B_\infty$. As also
$h_{\theta ^{-1}}(B_\infty ) = B_\infty$. As also ![]() $h_{\theta }(B_\infty ) = B_\infty$, we have
$h_{\theta }(B_\infty ) = B_\infty$, we have ![]() $h_\theta (D\cap J) = h_\theta (D)\cap J$. Thus,
$h_\theta (D\cap J) = h_\theta (D)\cap J$. Thus, ![]() $h_\theta$ is a symmetry of
$h_\theta$ is a symmetry of ![]() $J$.
$J$.
As the repelling periodic points of ![]() $f$ are dense in
$f$ are dense in ![]() $J$ we may assume that the centre of
$J$ we may assume that the centre of ![]() $D$ is a repelling fixed point of
$D$ is a repelling fixed point of ![]() $f$ (after possibly replacing
$f$ (after possibly replacing ![]() $f$ by an iterate of
$f$ by an iterate of ![]() $f$). Thus, there exists a holomorphic function
$f$). Thus, there exists a holomorphic function ![]() $F$ such that
$F$ such that
There exists a disc ![]() $D_0$ about 0 such that
$D_0$ about 0 such that ![]() $F(D_0) \subset D$ and
$F(D_0) \subset D$ and ![]() $F$ is bi-holomorphic onto its image. Setting
$F$ is bi-holomorphic onto its image. Setting ![]() $U = F(D_0)$ we see that a branch of the inverse of
$U = F(D_0)$ we see that a branch of the inverse of ![]() $f$ defined by
$f$ defined by ![]() $f^{-1}(z) = F(\lambda ^{-1}F^{-1}(z))$ is well-defined on
$f^{-1}(z) = F(\lambda ^{-1}F^{-1}(z))$ is well-defined on ![]() $U$ and it satisfies
$U$ and it satisfies ![]() $f^{-1}(U) \subset U$. Thus, we can define
$f^{-1}(U) \subset U$. Thus, we can define ![]() $h_{\theta ^{d}}(z)$ on
$h_{\theta ^{d}}(z)$ on ![]() $U$ by
$U$ by
As ![]() $h_\theta (J\cap U) = h_\theta (U) \cap J$ and
$h_\theta (J\cap U) = h_\theta (U) \cap J$ and ![]() $J$ is completely invariant under
$J$ is completely invariant under ![]() $f$ we have that
$f$ we have that ![]() $h_{\theta ^{d}}(U\cap J) = h_{\theta ^{d}}(U)\cap J$. Thus, the inductively constructed family
$h_{\theta ^{d}}(U\cap J) = h_{\theta ^{d}}(U)\cap J$. Thus, the inductively constructed family ![]() $H= \{g_n\}_{n \geq 0}$ with
$H= \{g_n\}_{n \geq 0}$ with ![]() $g_{n+1} = f\circ g_n\circ f^{-1}(z), g_0 = h_\theta$ is a family of symmetries of
$g_{n+1} = f\circ g_n\circ f^{-1}(z), g_0 = h_\theta$ is a family of symmetries of ![]() $J$. Now we prove that
$J$. Now we prove that ![]() $H$ is a normal family.
$H$ is a normal family.
We have that ![]() $U \cap B_\infty \subset V = \{g_f(z) \leq t\}$ for some fixed
$U \cap B_\infty \subset V = \{g_f(z) \leq t\}$ for some fixed ![]() $t > 0$ and, thus, that
$t > 0$ and, thus, that ![]() $g_n(U\cap B_\infty ) \subset V$ for all
$g_n(U\cap B_\infty ) \subset V$ for all ![]() $n \geq 0$. We also proved above that
$n \geq 0$. We also proved above that ![]() $g_n(\mathbb {C}\setminus B_\infty ) \subset \mathbb {C}\setminus B_\infty$ and, thus,
$g_n(\mathbb {C}\setminus B_\infty ) \subset \mathbb {C}\setminus B_\infty$ and, thus, ![]() $g_n(U) \subset V$ for all
$g_n(U) \subset V$ for all ![]() $n \geq 0$ and, thus,
$n \geq 0$ and, thus, ![]() $g_n$ is uniformly bounded on
$g_n$ is uniformly bounded on ![]() $U$. By Montel's theorem the family
$U$. By Montel's theorem the family ![]() $H$ is a normal family. Moreover, the set of rotations of the unit disc is a closed subset of the space of functions on the unit disc with respect to the sup-norm. Thus,
$H$ is a normal family. Moreover, the set of rotations of the unit disc is a closed subset of the space of functions on the unit disc with respect to the sup-norm. Thus, ![]() $g_n$ is a non-trivial normal family of symmetries of
$g_n$ is a non-trivial normal family of symmetries of ![]() $J$ in the sense of Levin. From his theorem [Reference LevinLev91] and [Reference Douady and HubbardDH93] it follows that
$J$ in the sense of Levin. From his theorem [Reference LevinLev91] and [Reference Douady and HubbardDH93] it follows that ![]() $f$ is exceptional.
$f$ is exceptional.
The next lemma is an addendum to the previous one, but it uses the precise classification of periodic varieties in the work of Medvedev and Scanlon [Reference Medvedev and ScanlonMS14]. For the following lemma we do not assume that the Julia set of ![]() $f$ is connected.
$f$ is connected.
Lemma 5.10 Suppose that ![]() $f$ is a non-exceptional polynomial of degree
$f$ is a non-exceptional polynomial of degree ![]() $d \geq 2$ and suppose that there exists an irreducible polynomial
$d \geq 2$ and suppose that there exists an irreducible polynomial ![]() $P \in \mathbb {C}[X,Y]\setminus \{0\}$ and a root of unity
$P \in \mathbb {C}[X,Y]\setminus \{0\}$ and a root of unity ![]() $\theta$ such that
$\theta$ such that ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ for all
$P(\Psi (z), \Psi (\theta z)) = 0$ for all ![]() $z \in D_R$. Then there exists a linear polynomial
$z \in D_R$. Then there exists a linear polynomial ![]() $L$ commuting with an iterate
$L$ commuting with an iterate ![]() $f^{\circ M}$ of
$f^{\circ M}$ of ![]() $f$ such that
$f$ such that ![]() $P$ divides
$P$ divides ![]() $f^{\circ M}(X) - L\circ f^{\circ M}(Y)$.
$f^{\circ M}(X) - L\circ f^{\circ M}(Y)$.
Proof. We first note that if ![]() $\theta \in \mu _{d^{\infty }}$, we can set
$\theta \in \mu _{d^{\infty }}$, we can set ![]() $L(X) = X$ and we are finished. We now assume that
$L(X) = X$ and we are finished. We now assume that ![]() $\theta \notin \mu _{d^{\infty }}$. As
$\theta \notin \mu _{d^{\infty }}$. As ![]() $\Psi (z), \Psi (\theta z)$ are algebraically dependent, so are
$\Psi (z), \Psi (\theta z)$ are algebraically dependent, so are ![]() $\Psi (z^{d^{n}}) = f^{\circ n}(\Psi (z)), \Psi (\theta ^{d^{n}} z^{d^{n}}) = f^{\circ n}(\Psi (\theta z))$ for every
$\Psi (z^{d^{n}}) = f^{\circ n}(\Psi (z)), \Psi (\theta ^{d^{n}} z^{d^{n}}) = f^{\circ n}(\Psi (\theta z))$ for every ![]() $n \in \mathbb {Z}_{\geq 0}$. Thus, picking
$n \in \mathbb {Z}_{\geq 0}$. Thus, picking ![]() $n$ large enough we may assume that the order of
$n$ large enough we may assume that the order of ![]() $\tilde {\theta } = \theta ^{d^{n}}$ is co-prime to
$\tilde {\theta } = \theta ^{d^{n}}$ is co-prime to ![]() $d$ (but larger than 1) and there exists an irreducible non-zero polynomial
$d$ (but larger than 1) and there exists an irreducible non-zero polynomial ![]() $\tilde {P}$ such that
$\tilde {P}$ such that ![]() $\tilde {P}(f^{\circ n}(\Psi (z)), f^{\circ n}(\Psi (\theta z)) = 0$. As
$\tilde {P}(f^{\circ n}(\Psi (z)), f^{\circ n}(\Psi (\theta z)) = 0$. As ![]() $\tilde {\theta }$ has order co-prime to
$\tilde {\theta }$ has order co-prime to ![]() $d$, there exists
$d$, there exists ![]() $N \geq 1$ such that
$N \geq 1$ such that ![]() $\tilde {\theta }^{d^{N}} = \tilde {\theta }$. We deduce that the curve defined by
$\tilde {\theta }^{d^{N}} = \tilde {\theta }$. We deduce that the curve defined by ![]() $\tilde {P}$ is invariant under the coordinate action of
$\tilde {P}$ is invariant under the coordinate action of ![]() $f^{\circ N}$. By [Reference Medvedev and ScanlonMS14, Theorem 6.24] there exists
$f^{\circ N}$. By [Reference Medvedev and ScanlonMS14, Theorem 6.24] there exists ![]() $\ell \in \mathbb {Z}_{\geq 0}$, a polynomial
$\ell \in \mathbb {Z}_{\geq 0}$, a polynomial ![]() $h$ of positive degree and a linear polynomial
$h$ of positive degree and a linear polynomial ![]() $L$ commuting with
$L$ commuting with ![]() $f^{\circ N}$ such that up to a constant
$f^{\circ N}$ such that up to a constant ![]() $\tilde {P} = Y -L\circ h^{\circ \ell }(X)$ or
$\tilde {P} = Y -L\circ h^{\circ \ell }(X)$ or ![]() $\tilde {P} = X -L\circ h^{\circ \ell }(Y)$. We may assume the former and if
$\tilde {P} = X -L\circ h^{\circ \ell }(Y)$. We may assume the former and if ![]() $\ell \geq 1$, it follows that the function
$\ell \geq 1$, it follows that the function
has meromorphic continuation to ![]() $\infty$ where it has a super-attracting fixed point of degree at least two. As
$\infty$ where it has a super-attracting fixed point of degree at least two. As ![]() $\Psi$ is one-to-one at infinity we get a contradiction and so
$\Psi$ is one-to-one at infinity we get a contradiction and so ![]() $\ell = 0$ and we obtain that
$\ell = 0$ and we obtain that ![]() $\tilde {P} = y - L(X)$ for
$\tilde {P} = y - L(X)$ for ![]() $L$ a linear polynomial satisfying
$L$ a linear polynomial satisfying ![]() $L\circ f^{\circ N} = f^{\circ N}\circ L$. Setting
$L\circ f^{\circ N} = f^{\circ N}\circ L$. Setting ![]() $M = N +n$, we conclude the proof.
$M = N +n$, we conclude the proof.
5.2 Proof of Theorem 3 for connected Julia sets
We recall that we may assume that ![]() $\mathcal {C}$ is defined by a polynomial
$\mathcal {C}$ is defined by a polynomial ![]() $P$ that satisfies
$P$ that satisfies ![]() $\partial _XP\partial _YP \neq 0$. If
$\partial _XP\partial _YP \neq 0$. If ![]() $\mathcal {C}$ intersects
$\mathcal {C}$ intersects ![]() $L_r^{2}$ in infinitely many points, we can find
$L_r^{2}$ in infinitely many points, we can find ![]() $\mathcal {B}$ as in (15). From Proposition 5.8 and Lemma 5.9 we deduce that
$\mathcal {B}$ as in (15). From Proposition 5.8 and Lemma 5.9 we deduce that ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ identically on
$P(\Psi (z), \Psi (\theta z)) = 0$ identically on ![]() $D$ for some
$D$ for some ![]() $\theta \in \mu _{\infty }$. Finally Lemma 5.10 finishes the proof.
$\theta \in \mu _{\infty }$. Finally Lemma 5.10 finishes the proof.
6. Disconnected Julia sets
In this section we consider as in the last section a monic complex polynomial ![]() $f\in \mathbb {C}[X]$ of degree
$f\in \mathbb {C}[X]$ of degree ![]() $d \geq 2$. However, in this section we suppose that its Julia set is disconnected. (In particular,
$d \geq 2$. However, in this section we suppose that its Julia set is disconnected. (In particular, ![]() $f$ is non-exceptional.)
$f$ is non-exceptional.)
We pause quickly to discuss the proof strategy. We use the same strategy as in the last section but instead of using the rigidity theorems of Fatou and Levin, we rely on investigations of the monodromy action on ![]() $\Psi$ as discussed in the following. In this sense our proof is independent of previous work on the geometry of Julia sets and introduces a new perspective. We can make the proof also independent of Fatou's theorem although we do not explicitly point it out in the following. This shows that monodromy contains ‘enough information’ about the geometric structure of the dynamical system.
$\Psi$ as discussed in the following. In this sense our proof is independent of previous work on the geometry of Julia sets and introduces a new perspective. We can make the proof also independent of Fatou's theorem although we do not explicitly point it out in the following. This shows that monodromy contains ‘enough information’ about the geometric structure of the dynamical system.
If the Julia set of ![]() $f$ is disconnected, then the basin of infinity
$f$ is disconnected, then the basin of infinity ![]() $B_\infty$ contains a critical point of
$B_\infty$ contains a critical point of ![]() $f$. Thus, it is useful to define
$f$. Thus, it is useful to define
and the inverse images
We can compute ![]() $R$ using
$R$ using ![]() $C_{\text {crit}}$. Namely
$C_{\text {crit}}$. Namely
and it is immediate that we can continue ![]() $\Psi$ analytically to
$\Psi$ analytically to
using the relation
but not to a larger disc. However, we can continue ![]() $\Psi$ along certain paths beyond
$\Psi$ along certain paths beyond ![]() $D_R$ but not as a global analytic function. In order to describe the situation more precisely, we introduce some terminology. We denote by
$D_R$ but not as a global analytic function. In order to describe the situation more precisely, we introduce some terminology. We denote by ![]() $D_R^{*} = D_R\setminus \{0\}$ and by
$D_R^{*} = D_R\setminus \{0\}$ and by ![]() $D_n^{*} = D^{*}_{R^{1/d^{n}}}$. We define an auxiliary set
$D_n^{*} = D^{*}_{R^{1/d^{n}}}$. We define an auxiliary set
where ![]() $n_c \in \mathbb {Z}_{\geq 1}$ is minimal among the integers
$n_c \in \mathbb {Z}_{\geq 1}$ is minimal among the integers ![]() $n$ such that
$n$ such that ![]() $f^{\circ n}(c) \in \Psi (D_R^{*})$. For a non-negative integer
$f^{\circ n}(c) \in \Psi (D_R^{*})$. For a non-negative integer ![]() $n$ we define the set
$n$ we define the set ![]() $S_n$ to be the local analytic functions
$S_n$ to be the local analytic functions ![]() $\tilde {\Psi }$ on
$\tilde {\Psi }$ on ![]() $D_n = D^{*}_n \setminus U_n$, where
$D_n = D^{*}_n \setminus U_n$, where ![]() $U_n = \{\zeta z; z\in \bigcup _{m = 1}^{n}E_m, \zeta \in \mu _{d^{n}}\}$, that satisfy
$U_n = \{\zeta z; z\in \bigcup _{m = 1}^{n}E_m, \zeta \in \mu _{d^{n}}\}$, that satisfy
Note that the left-hand side of (16) is a well-defined analytic function. We can interpret ![]() $\tilde {\Psi }$ as the algebraic function
$\tilde {\Psi }$ as the algebraic function ![]() $f^{-\circ n}(Y)$ in the variable
$f^{-\circ n}(Y)$ in the variable ![]() $Y = \Psi (z^{d^{n}})$. Note that we can restrict the solutions to
$Y = \Psi (z^{d^{n}})$. Note that we can restrict the solutions to ![]() $D^{*}_0 = D^{*}_R$ where they are analytic and we see that a complete set of solutions of (16) is given by the set of functions
$D^{*}_0 = D^{*}_R$ where they are analytic and we see that a complete set of solutions of (16) is given by the set of functions ![]() $\{\Psi (\zeta z); \zeta \in \mu _{d^{n}}\}$.
$\{\Psi (\zeta z); \zeta \in \mu _{d^{n}}\}$.
From the interpretation of ![]() $\tilde {\Psi }$ as an algebraic function in
$\tilde {\Psi }$ as an algebraic function in ![]() $\Psi (z)$ we see that each function element on
$\Psi (z)$ we see that each function element on ![]() $D_n$ is given by a triple
$D_n$ is given by a triple ![]() $(\zeta, D, \gamma )$ where
$(\zeta, D, \gamma )$ where ![]() $D$ is an open disc in
$D$ is an open disc in ![]() $D_n, \gamma$ a path from
$D_n, \gamma$ a path from ![]() $D_0$ to
$D_0$ to ![]() $D$ and the function
$D$ and the function ![]() $\tilde {\Psi }$ on
$\tilde {\Psi }$ on ![]() $D$ is the continuation of
$D$ is the continuation of ![]() $\Psi (\zeta z)$ from
$\Psi (\zeta z)$ from ![]() $_0$ to
$_0$ to ![]() $D$ along
$D$ along ![]() $\gamma$. Moreover at each point
$\gamma$. Moreover at each point ![]() $z_0 \in E_n$ restricting a function element
$z_0 \in E_n$ restricting a function element ![]() $\tilde {\Psi }$ to a disc
$\tilde {\Psi }$ to a disc ![]() $D$ centred at
$D$ centred at ![]() $z_0$ we obtain a Puiseux expansion of
$z_0$ we obtain a Puiseux expansion of ![]() $\tilde {\Psi }$ converging on
$\tilde {\Psi }$ converging on ![]() $D$ and a well-defined value
$D$ and a well-defined value ![]() $\tilde {\Psi }(z_0)$. As each function element
$\tilde {\Psi }(z_0)$. As each function element ![]() $\tilde {\Psi }$ is a continuation of
$\tilde {\Psi }$ is a continuation of ![]() $\Psi (\zeta z)$ for some
$\Psi (\zeta z)$ for some ![]() $\zeta \in \mu _{d^{n}}$ it follows that continuing
$\zeta \in \mu _{d^{n}}$ it follows that continuing ![]() $\tilde {\Psi }$ along a simple closed loop around
$\tilde {\Psi }$ along a simple closed loop around ![]() $z_0$ sends
$z_0$ sends ![]() $\tilde {\Psi }(z)$ to
$\tilde {\Psi }(z)$ to ![]() $\tilde {\Psi }(\zeta z)$ for some
$\tilde {\Psi }(\zeta z)$ for some ![]() $\zeta \in \mu _{d^{n}}$ where
$\zeta \in \mu _{d^{n}}$ where ![]() $\tilde {\Psi }(\zeta z)$ is given by the triple
$\tilde {\Psi }(\zeta z)$ is given by the triple ![]() $(\zeta \zeta _1, D, \gamma )$ when
$(\zeta \zeta _1, D, \gamma )$ when ![]() $\tilde {\Psi }$ is given by
$\tilde {\Psi }$ is given by ![]() $(\zeta _1, D, \gamma )$. Now if
$(\zeta _1, D, \gamma )$. Now if ![]() $\tilde {\Psi }(z_0) \in C_n$, then the monodromy action given by loops in
$\tilde {\Psi }(z_0) \in C_n$, then the monodromy action given by loops in ![]() $D$ around
$D$ around ![]() $z_0$ we just described is non-trivial. We can say something a bit more precise for continuations of
$z_0$ we just described is non-trivial. We can say something a bit more precise for continuations of ![]() $\Psi$ to
$\Psi$ to ![]() $D_n$. For this we define the set
$D_n$. For this we define the set ![]() $S_{n,\Psi }$ to be the set of locally analytic functions on
$S_{n,\Psi }$ to be the set of locally analytic functions on ![]() $D_n$ that are continuations of
$D_n$ that are continuations of ![]() $\Psi$. Clearly
$\Psi$. Clearly ![]() $S_{n, \Psi } \subset S_n$ and we write
$S_{n, \Psi } \subset S_n$ and we write ![]() $\Psi$ for a continuation of
$\Psi$ for a continuation of ![]() $\Psi$ to
$\Psi$ to ![]() $D_n$. We have the following lemma.
$D_n$. We have the following lemma.
Lemma 6.1 Let ![]() $\Psi$ be a continuation of
$\Psi$ be a continuation of ![]() $\Psi$ (on
$\Psi$ (on ![]() $D_0)$ along a path in
$D_0)$ along a path in ![]() $D_n$ to a small disc
$D_n$ to a small disc ![]() $\tilde {D}$ centred at
$\tilde {D}$ centred at ![]() $z_0 \in E_n$ (as an algebraic function of
$z_0 \in E_n$ (as an algebraic function of ![]() $\Psi (z^{d^{n}})$) and suppose that
$\Psi (z^{d^{n}})$) and suppose that ![]() $\Psi (z_0) \in C_n$. Continuing
$\Psi (z_0) \in C_n$. Continuing ![]() $\Psi$ restricted to a disc
$\Psi$ restricted to a disc ![]() $D \subset \tilde {D}\setminus \{z_0\}$ along a small loop around
$D \subset \tilde {D}\setminus \{z_0\}$ along a small loop around ![]() $z_0$ sends
$z_0$ sends ![]() $\Psi (z)$ to
$\Psi (z)$ to ![]() $\Psi (\zeta z)$ for
$\Psi (\zeta z)$ for ![]() $\zeta \in \mu _{d^{\infty }}$ of order at least
$\zeta \in \mu _{d^{\infty }}$ of order at least ![]() $2^{n}$.
$2^{n}$.
Proof. We prove this by induction on ![]() $n$. First consider
$n$. First consider
on ![]() $D_1$ and recall that
$D_1$ and recall that ![]() $S_{1,\Psi } \subset S_1$. Now if
$S_{1,\Psi } \subset S_1$. Now if ![]() $\Psi (z_0) \in C_1$, then
$\Psi (z_0) \in C_1$, then ![]() $f'(\Psi (z_0)) = 0$ and, thus, the monodromy action on
$f'(\Psi (z_0)) = 0$ and, thus, the monodromy action on ![]() $\Psi$ is non-trivial. It follows that continuing
$\Psi$ is non-trivial. It follows that continuing ![]() $\Psi$ along a simple closed loop around
$\Psi$ along a simple closed loop around ![]() $z_0$ sends
$z_0$ sends ![]() $\Psi (z)$ to
$\Psi (z)$ to ![]() $\Psi (\zeta z)$ where
$\Psi (\zeta z)$ where ![]() $\zeta \in \mu _d$ is of order at least two.
$\zeta \in \mu _d$ is of order at least two.
Now consider
on ![]() $D_n$ for
$D_n$ for ![]() $n \geq 2$ and
$n \geq 2$ and ![]() $z_0 \in E_n$ such that
$z_0 \in E_n$ such that ![]() $\Psi (z_0) \in C_n$ (for the continuation that we consider). Making the substitution
$\Psi (z_0) \in C_n$ (for the continuation that we consider). Making the substitution ![]() $w = z^{d}$ it follows from
$w = z^{d}$ it follows from ![]() $\Psi (z^{d}) = f(\Psi (z))$ that
$\Psi (z^{d}) = f(\Psi (z))$ that ![]() $\Psi (z^{d^{n}}) = f^{\circ n-1}(\Psi (z^{d}))$. Noting that
$\Psi (z^{d^{n}}) = f^{\circ n-1}(\Psi (z^{d}))$. Noting that ![]() $z_0^{d} \in E_{n-1}, \Psi (z_0^{d}) \in C_{n-1}$ we deduce that continuing
$z_0^{d} \in E_{n-1}, \Psi (z_0^{d}) \in C_{n-1}$ we deduce that continuing ![]() $\Psi (w)$ around
$\Psi (w)$ around ![]() $z_0$ sends
$z_0$ sends ![]() $\Psi (w)$ to
$\Psi (w)$ to ![]() $\zeta _1 w$ with
$\zeta _1 w$ with ![]() $\zeta _1 \in \mu _{d^{n-1}}$ of order at least
$\zeta _1 \in \mu _{d^{n-1}}$ of order at least ![]() $2^{n-1}$. Moreover, continuing
$2^{n-1}$. Moreover, continuing ![]() $\Psi$ around
$\Psi$ around ![]() $z_0$ sends
$z_0$ sends ![]() $\Psi (z)$ to
$\Psi (z)$ to ![]() $\Psi (\zeta _2 z)$ with
$\Psi (\zeta _2 z)$ with ![]() $\zeta _2 \in \mu _{d^{n}}$. From
$\zeta _2 \in \mu _{d^{n}}$. From ![]() $\Psi (z^{d})= f(\Psi (z))$ follows that
$\Psi (z^{d})= f(\Psi (z))$ follows that ![]() $\Psi (\zeta _1 z^{d}) = \Psi (\zeta _2^{d}z^{d})$ and, thus,
$\Psi (\zeta _1 z^{d}) = \Psi (\zeta _2^{d}z^{d})$ and, thus, ![]() $\zeta _2^{d} = \zeta _1$ and
$\zeta _2^{d} = \zeta _1$ and ![]() $\zeta _2$ has order at least
$\zeta _2$ has order at least ![]() $2^{n}$.
$2^{n}$.
6.1 Puiseux expansions
As we use Puiseux's theorem in many of the proofs, we give the version we are going to use as a lemma.
Lemma 6.2 (Puiseux)
Let ![]() $\mathcal {G}$ be an analytic function on
$\mathcal {G}$ be an analytic function on ![]() $D^{2}$ that satisfies
$D^{2}$ that satisfies ![]() $\mathcal {G}(0,0) = 0$. There exists an integer
$\mathcal {G}(0,0) = 0$. There exists an integer ![]() $N \geq 1$ and
$N \geq 1$ and ![]() $\epsilon > 0$ such that for any integer
$\epsilon > 0$ such that for any integer ![]() $M$ divisible by
$M$ divisible by ![]() $N$ and any analytic function
$N$ and any analytic function ![]() $w:D \rightarrow D_\epsilon$ where
$w:D \rightarrow D_\epsilon$ where ![]() $D$ is a disc about a point
$D$ is a disc about a point ![]() $x_0 \in \mathbb {C}$, that satisfies
$x_0 \in \mathbb {C}$, that satisfies ![]() $w(x_0) = 0$ and whose first
$w(x_0) = 0$ and whose first ![]() $M-1$ derivatives vanish at
$M-1$ derivatives vanish at ![]() $x_0$ there exists an analytic function
$x_0$ there exists an analytic function ![]() $h_w$ on
$h_w$ on ![]() $D$ such that
$D$ such that ![]() $\mathcal {G}(w(x), h_w(x))= 0$ for all
$\mathcal {G}(w(x), h_w(x))= 0$ for all ![]() $x \in D$.
$x \in D$.
Proof. This follows from [Reference ZoladekZol06, The Puiseux Theorem, p. 28]. We only need to note that ![]() $w$ sends simple loops about
$w$ sends simple loops about ![]() $x_0$ to loops winding
$x_0$ to loops winding ![]() $M$ times about
$M$ times about ![]() $0$.
$0$.
We describe the Puiseux expansions of ![]() $\Psi$ a bit more concretely in what follows.
$\Psi$ a bit more concretely in what follows.
Lemma 6.3 At each point ![]() $z_0 \in D_n^{*}$ and each
$z_0 \in D_n^{*}$ and each ![]() $w_0 \in \{f^{-\circ n}(\Psi (z_0^{d^{n}}))\}$ there exists a disc
$w_0 \in \{f^{-\circ n}(\Psi (z_0^{d^{n}}))\}$ there exists a disc ![]() $D$ about
$D$ about ![]() $z_0$, a positive integer
$z_0$, a positive integer ![]() $N$ and an analytic function
$N$ and an analytic function ![]() $\Psi _N$ on
$\Psi _N$ on ![]() $D$ such that
$D$ such that ![]() $S= \{z \in D; (z_0 +(z-z_0)^{N}, \Psi _N(z))\}$ is the set of
$S= \{z \in D; (z_0 +(z-z_0)^{N}, \Psi _N(z))\}$ is the set of ![]() $(z,w) \in \mathbb {C}^{2}$ such that
$(z,w) \in \mathbb {C}^{2}$ such that
Proof. Setting ![]() $\mathcal {G} = \Psi (z^{d^{n}}) - f^{\circ n}(w)$ in Lemma 6.2 we obtain the claim after noting that the zero set of
$\mathcal {G} = \Psi (z^{d^{n}}) - f^{\circ n}(w)$ in Lemma 6.2 we obtain the claim after noting that the zero set of ![]() $\mathcal {G}$ is smooth and irreducible in a neighbourhood of each point
$\mathcal {G}$ is smooth and irreducible in a neighbourhood of each point ![]() $(z_0,w_0)\in (D_n^{*})^{2}$.
$(z_0,w_0)\in (D_n^{*})^{2}$.
Similarly as in the previous section we define
Recall that ![]() $\phi \in D_R\cap \mathbb {R}$. For any
$\phi \in D_R\cap \mathbb {R}$. For any ![]() $a < b$ we define
$a < b$ we define ![]() $A(a,b) = \{z \in \mathbb {C}; a<|z|< b\}$. There exists
$A(a,b) = \{z \in \mathbb {C}; a<|z|< b\}$. There exists ![]() $\epsilon > 0$ such that the function
$\epsilon > 0$ such that the function ![]() $\mu$ defined by
$\mu$ defined by
is well-defined on ![]() $\Psi (A(\phi -\epsilon, \phi + \epsilon ))$. We start this section by investigating various properties of this function. From the discussion of the last section it already follows that it cannot be defined globally on
$\Psi (A(\phi -\epsilon, \phi + \epsilon ))$. We start this section by investigating various properties of this function. From the discussion of the last section it already follows that it cannot be defined globally on ![]() $B_\infty$, but we can make sense of it as a locally defined function on paths. We have the following lemma.
$B_\infty$, but we can make sense of it as a locally defined function on paths. We have the following lemma.
Lemma 6.4 Let ![]() $\gamma :[0,1)\rightarrow \mathcal {F}$ be a path with
$\gamma :[0,1)\rightarrow \mathcal {F}$ be a path with ![]() $\gamma (0) \in \Psi (S^{\phi })$. We can continue
$\gamma (0) \in \Psi (S^{\phi })$. We can continue ![]() $\mu$ along this path and
$\mu$ along this path and ![]() $\mu _{|\gamma |}$ is continuous and has a Puiseux expansion at each point of
$\mu _{|\gamma |}$ is continuous and has a Puiseux expansion at each point of ![]() $|\gamma |$. Moreover, we can continue
$|\gamma |$. Moreover, we can continue ![]() $\mu ^{h}$ along
$\mu ^{h}$ along ![]() $\mu \circ \gamma$ such that it holds that
$\mu \circ \gamma$ such that it holds that ![]() $\mu ^{h}\circ \mu (z) = z$ on
$\mu ^{h}\circ \mu (z) = z$ on ![]() $|\gamma |$.
$|\gamma |$.
Proof. It is clear that the claim is true for ![]() $\gamma$ restricted to
$\gamma$ restricted to ![]() $[0,T)$ for some
$[0,T)$ for some ![]() $T>0$. We pick
$T>0$. We pick ![]() $T$ maximal such that the claim is true and are going to show that
$T$ maximal such that the claim is true and are going to show that ![]() $T = 1$. We prove this by contradiction. Suppose that
$T = 1$. We prove this by contradiction. Suppose that ![]() $T <1$. Then
$T <1$. Then ![]() $\gamma (T) = x_0 \in \mathcal {F}$ and
$\gamma (T) = x_0 \in \mathcal {F}$ and ![]() $\mu$ has a Puiseux expansion at
$\mu$ has a Puiseux expansion at ![]() $x_0$. Let
$x_0$. Let ![]() $D$ be the disc at which the function
$D$ be the disc at which the function ![]() $\Psi _N$ in Lemma 6.3 is analytic. Moreover,
$\Psi _N$ in Lemma 6.3 is analytic. Moreover, ![]() $\mu ^{h}$ has a Puiseux expansion at
$\mu ^{h}$ has a Puiseux expansion at ![]() $\mu (x_0)$ where the value
$\mu (x_0)$ where the value ![]() $\mu (x_0)$ is well-defined by the definition of the Puiseux expansion. We can shrink
$\mu (x_0)$ is well-defined by the definition of the Puiseux expansion. We can shrink ![]() $D$ such that
$D$ such that ![]() $\mu (D)$ is contained in a disc on which the Puiseux expansion of
$\mu (D)$ is contained in a disc on which the Puiseux expansion of ![]() $\mu ^{h}$ at
$\mu ^{h}$ at ![]() $\mu (x_0)$ converges. Let
$\mu (x_0)$ converges. Let ![]() $T' < T$ be such that
$T' < T$ be such that ![]() $\gamma (T') \in \partial D$ and such that
$\gamma (T') \in \partial D$ and such that ![]() $\gamma (t) \notin \partial D$ for any
$\gamma (t) \notin \partial D$ for any ![]() $T'< t< T$. Then we can continue
$T'< t< T$. Then we can continue ![]() $\mu$ along any path that consists of
$\mu$ along any path that consists of ![]() $\gamma$ restricted to
$\gamma$ restricted to ![]() $[0,T']$ composed with any path in
$[0,T']$ composed with any path in ![]() $D\setminus \{x_0\}$. Along any such path it holds that
$D\setminus \{x_0\}$. Along any such path it holds that ![]() $\mu ^{h}\circ \mu (z) = z$. For
$\mu ^{h}\circ \mu (z) = z$. For ![]() $D$ sufficiently small
$D$ sufficiently small ![]() $D \cap |\gamma |$ consists of two connected open components
$D \cap |\gamma |$ consists of two connected open components ![]() $D_1,D_2$ and
$D_1,D_2$ and ![]() $\mu$ is analytic on
$\mu$ is analytic on ![]() $D_1$ and
$D_1$ and ![]() $\mu ^{h}$ is analytic on
$\mu ^{h}$ is analytic on ![]() $\mu (D_1)$. On
$\mu (D_1)$. On ![]() $D_1$ it holds that
$D_1$ it holds that ![]() $\mu ^{h}\circ \mu (z) = z$ and then, by continuity, also on
$\mu ^{h}\circ \mu (z) = z$ and then, by continuity, also on ![]() $|\gamma |$ if we continue
$|\gamma |$ if we continue ![]() $\mu$ to
$\mu$ to ![]() $|\gamma |$ from
$|\gamma |$ from ![]() $D_1$. Thus, we can continue
$D_1$. Thus, we can continue ![]() $\mu$ with the properties demanded of the Lemma to
$\mu$ with the properties demanded of the Lemma to ![]() $\gamma$ restricted to
$\gamma$ restricted to ![]() $[0,T^{\prime \prime })$ with
$[0,T^{\prime \prime })$ with ![]() $T'' > T$. A contradiction.
$T'' > T$. A contradiction.
Lemma 6.5 Let ![]() $P_1,P_2 \in \mathbb {C}[X,Y]$ and suppose that there exists a non-constant analytic function
$P_1,P_2 \in \mathbb {C}[X,Y]$ and suppose that there exists a non-constant analytic function ![]() $h$ in a neighbourhood of
$h$ in a neighbourhood of ![]() $x_0 \in \Psi (S^{\phi })$ such that
$x_0 \in \Psi (S^{\phi })$ such that
and ![]() $h(x_0) = y_0 \in \Psi (S^{\phi })$. Suppose there is a path
$h(x_0) = y_0 \in \Psi (S^{\phi })$. Suppose there is a path ![]() $\gamma : [0,1) \rightarrow \mathcal {F} \times \mathcal {F}$ with
$\gamma : [0,1) \rightarrow \mathcal {F} \times \mathcal {F}$ with ![]() $\gamma (0) = (x_0,y_0) \in \Psi (S^{\phi })^{2}$ and such that
$\gamma (0) = (x_0,y_0) \in \Psi (S^{\phi })^{2}$ and such that ![]() $P_1\circ \gamma = 0$. Then for any continuation of
$P_1\circ \gamma = 0$. Then for any continuation of ![]() $(\mu, \mu )$ along
$(\mu, \mu )$ along ![]() $\gamma$, it holds that
$\gamma$, it holds that ![]() $P_2(\mu (x),\mu (y)) = 0$ for all
$P_2(\mu (x),\mu (y)) = 0$ for all ![]() $(x,y) \in |\gamma |$.
$(x,y) \in |\gamma |$.
Proof. Let ![]() $T$ be maximal such that the claim is true for
$T$ be maximal such that the claim is true for ![]() $\gamma$ restricted to
$\gamma$ restricted to ![]() $[0,T)$. By assumption
$[0,T)$. By assumption ![]() $T > 0$ and we are going to show that
$T > 0$ and we are going to show that ![]() $T = 1$. If
$T = 1$. If ![]() $T < 1$, then
$T < 1$, then ![]() $\gamma (T) \in \mathcal {F}$ and we can set
$\gamma (T) \in \mathcal {F}$ and we can set ![]() $x_0 = \gamma (T)$ for
$x_0 = \gamma (T)$ for ![]() $x_0$ as in Lemma 6.4. By Lemmas 6.2 and 6.4 there exists a positive integer
$x_0$ as in Lemma 6.4. By Lemmas 6.2 and 6.4 there exists a positive integer ![]() $N$, analytic functions
$N$, analytic functions ![]() $h_{N}, \mu _{N_1}$ in a neighbourhood of
$h_{N}, \mu _{N_1}$ in a neighbourhood of ![]() $x_0$ and an analytic function
$x_0$ and an analytic function ![]() $\mu _{N_2}$ in a neighbourhood of
$\mu _{N_2}$ in a neighbourhood of ![]() $h(x_0)$ as well as
$h(x_0)$ as well as ![]() $\epsilon > 0$ such that
$\epsilon > 0$ such that
 \begin{align*} \mu_{N_1}(y) & = \mu(x_0 + (y-x_0)^{N}),\\ h_{N}(y) & = h(x_0 + (y-x_0)^{N}), \\ \mu_{N_2}(h_N(y)) & = \mu(h(y_0 + (x-y_0)^{N})) \end{align*}
\begin{align*} \mu_{N_1}(y) & = \mu(x_0 + (y-x_0)^{N}),\\ h_{N}(y) & = h(x_0 + (y-x_0)^{N}), \\ \mu_{N_2}(h_N(y)) & = \mu(h(y_0 + (x-y_0)^{N})) \end{align*}
for all ![]() $y$ satisfying
$y$ satisfying ![]() $x_0 + (y-y_0)^{N} \in \gamma (T-\epsilon, T)$. Thus, we can continue (17) by
$x_0 + (y-y_0)^{N} \in \gamma (T-\epsilon, T)$. Thus, we can continue (17) by
to a neighbourhood of ![]() $x_0$. This is a contradiction.
$x_0$. This is a contradiction.
Now we record an analogue of Lemma 5.2.
Lemma 6.6 Let ![]() $\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ be a path such that
$\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ be a path such that ![]() $\gamma ([0,1)) \subset \mathcal {F}$ and
$\gamma ([0,1)) \subset \mathcal {F}$ and ![]() $\gamma (0) \in \Psi (S^{\phi }), \gamma (1) \in \Psi (S^{\phi ^{2}})$. Then for any limit point
$\gamma (0) \in \Psi (S^{\phi }), \gamma (1) \in \Psi (S^{\phi ^{2}})$. Then for any limit point ![]() $c$ of
$c$ of ![]() $\mu \circ \gamma (t)$ as
$\mu \circ \gamma (t)$ as ![]() $t \rightarrow 1$, it holds that
$t \rightarrow 1$, it holds that ![]() $c \in J^{h}$. Moreover, for any path
$c \in J^{h}$. Moreover, for any path ![]() $\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ with
$\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ with ![]() $\gamma ([0,1))\subset \mathcal {F}$ and
$\gamma ([0,1))\subset \mathcal {F}$ and ![]() $\gamma (0) \in \Psi (S^{\phi }),\ \gamma (1) \in J$, we have that for any limit point
$\gamma (0) \in \Psi (S^{\phi }),\ \gamma (1) \in J$, we have that for any limit point ![]() $c$ of
$c$ of ![]() $\mu \circ \gamma$ it holds that
$\mu \circ \gamma$ it holds that ![]() $c \in \Psi ^{h}(S^{\phi ^{2}})$.
$c \in \Psi ^{h}(S^{\phi ^{2}})$.
Proof. This follows from Lemma 6.4.
6.2 Analytic continuation
We assume that for ![]() $\exp (-r) = \phi,\ \mathcal {C}\cap L_r^{2}$ contains an analytic arc
$\exp (-r) = \phi,\ \mathcal {C}\cap L_r^{2}$ contains an analytic arc ![]() $\mathcal {A}$. We let
$\mathcal {A}$. We let ![]() $C_0$ be the connected component of
$C_0$ be the connected component of ![]() $\mathcal {C}\cap \mathcal {F}^{2}$ containing
$\mathcal {C}\cap \mathcal {F}^{2}$ containing ![]() $\mathcal {A}$. We recall that relation (15) holds on
$\mathcal {A}$. We recall that relation (15) holds on ![]() $\mathcal {A}$. Now we prove an analogue of Lemma 5.3 for disconnected Julia sets.
$\mathcal {A}$. Now we prove an analogue of Lemma 5.3 for disconnected Julia sets.
Lemma 6.7 Suppose that ![]() $\overline {C_0}\cap \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ is not empty. Then there exists
$\overline {C_0}\cap \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F}$ is not empty. Then there exists ![]() $x_0 \in \Psi (S^{\phi ^{2}})$ such that we can continue
$x_0 \in \Psi (S^{\phi ^{2}})$ such that we can continue ![]() $\mu$ analytically along a path
$\mu$ analytically along a path ![]() $\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ with
$\gamma :[0,1] \rightarrow \bar {\mathcal {F}}$ with ![]() $\gamma ([0,1)) \subset \mathcal {F}$,
$\gamma ([0,1)) \subset \mathcal {F}$, ![]() $\gamma (0) \in \Psi (S^{\phi }),\ \gamma (1) = x_0$.
$\gamma (0) \in \Psi (S^{\phi }),\ \gamma (1) = x_0$.
Proof. We first note that we can continue ![]() $\mu$ to a point on
$\mu$ to a point on ![]() $\Psi (S^{\phi ^{2}})$ if and only if we can continue
$\Psi (S^{\phi ^{2}})$ if and only if we can continue ![]() $\mu ^{h}$ to a point on
$\mu ^{h}$ to a point on ![]() $\Psi ^{h}(S^{\phi ^{2}})$.
$\Psi ^{h}(S^{\phi ^{2}})$.
From the relation (15) and Lemma 6.5 follows that there exists a path ![]() $\tilde {\gamma }:[0,1]\rightarrow \bar {\mathcal {F}}^{2}$,
$\tilde {\gamma }:[0,1]\rightarrow \bar {\mathcal {F}}^{2}$, ![]() $\tilde {\gamma }(0) \in \Psi (S^{\phi })^{2}$,
$\tilde {\gamma }(0) \in \Psi (S^{\phi })^{2}$, ![]() $\gamma (1) \in \partial \mathcal {F}\times \partial \mathcal {F}$ such that
$\gamma (1) \in \partial \mathcal {F}\times \partial \mathcal {F}$ such that
for all ![]() $(x,y) \in |\tilde {\gamma }|$ and by Lemma 6.4 it follows that
$(x,y) \in |\tilde {\gamma }|$ and by Lemma 6.4 it follows that ![]() $P(\mu ^{h}\circ x, \mu ^{h} \circ y) = P^{h}(x,y) = 0$ for all
$P(\mu ^{h}\circ x, \mu ^{h} \circ y) = P^{h}(x,y) = 0$ for all ![]() $(x,y) \in \mu \circ \tilde {\gamma }$. (Here we have taken the appropriate continuations of
$(x,y) \in \mu \circ \tilde {\gamma }$. (Here we have taken the appropriate continuations of ![]() $\mu ^{h}$ as described in Lemma 6.4). Thus, up to replacing
$\mu ^{h}$ as described in Lemma 6.4). Thus, up to replacing ![]() $P$ by
$P$ by ![]() $P^{h}$ and permuting
$P^{h}$ and permuting ![]() $(x,y)$ we may assume that there exists
$(x,y)$ we may assume that there exists ![]() $(x_0,y_0) \in \bar {C}_0\cap \Psi (S^{\phi ^{2}})\times \mathcal {F}$ and as
$(x_0,y_0) \in \bar {C}_0\cap \Psi (S^{\phi ^{2}})\times \mathcal {F}$ and as ![]() $\Psi (S^{\phi ^{2}})$ does not contain isolated points and
$\Psi (S^{\phi ^{2}})$ does not contain isolated points and ![]() $\mathcal {F}$ is open we may even assume that
$\mathcal {F}$ is open we may even assume that ![]() $\partial _YP(x_0,y_0)\partial _X P(x,\mu (y_0)) \neq 0$ for all
$\partial _YP(x_0,y_0)\partial _X P(x,\mu (y_0)) \neq 0$ for all ![]() $x$ such that
$x$ such that ![]() $P(x,\mu (y_0)) = 0$. Thus, there exists an analytic function
$P(x,\mu (y_0)) = 0$. Thus, there exists an analytic function ![]() $g$ on a disc
$g$ on a disc ![]() $D$ centred at
$D$ centred at ![]() $x_0$ such that
$x_0$ such that
for all ![]() $x \in D_1 \subset \mathcal {F}$, where
$x \in D_1 \subset \mathcal {F}$, where ![]() $D_1$ is such that
$D_1$ is such that ![]() $D\setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with
$D\setminus \Psi (S^{\phi ^{2}}) = D_1\cup D_2$ with ![]() $D_2 \subset B_\infty \setminus \mathcal {F}$. Let
$D_2 \subset B_\infty \setminus \mathcal {F}$. Let ![]() $\mu _0$ be some limit point of
$\mu _0$ be some limit point of ![]() $\mu (x)$ for
$\mu (x)$ for ![]() $x \rightarrow x_0, x \in D_1$. There exists an analytic function
$x \rightarrow x_0, x \in D_1$. There exists an analytic function ![]() $\tilde {g}$ on a disc
$\tilde {g}$ on a disc ![]() $\tilde {D}$ centred at
$\tilde {D}$ centred at ![]() $\mu \circ g(x_0)$ such that
$\mu \circ g(x_0)$ such that ![]() $\tilde {g}(\mu \circ g(x_0)) = \mu _0$ and
$\tilde {g}(\mu \circ g(x_0)) = \mu _0$ and ![]() $P^{h}(\tilde {g}(z),z ) = 0$ for all
$P^{h}(\tilde {g}(z),z ) = 0$ for all ![]() $z \in \tilde {D}$. We can shrink
$z \in \tilde {D}$. We can shrink ![]() $D$ sufficiently such that
$D$ sufficiently such that ![]() $\mu \circ g(D)\subset \tilde {D}$ and we see that
$\mu \circ g(D)\subset \tilde {D}$ and we see that ![]() $\tilde {g}\circ \mu \circ g$ is a continuation of
$\tilde {g}\circ \mu \circ g$ is a continuation of ![]() $\mu$ to
$\mu$ to ![]() $D$.
$D$.
As a direct consequence of the previous lemma we obtain the analogue of Corollary 5.5.
Corollary 6.8 The set ![]() $\overline {C_0}\cap (\partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty.
$\overline {C_0}\cap (\partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty.
Proof. Suppose for contradiction that ![]() $\bar {C}_0\cap (\partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is not empty. By Lemma 6.7 we can continue
$\bar {C}_0\cap (\partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is not empty. By Lemma 6.7 we can continue ![]() $\mu$ analytically to a disc
$\mu$ analytically to a disc ![]() $D$ centred at a point of
$D$ centred at a point of ![]() $\Psi (S^{\phi ^{2}})$.
$\Psi (S^{\phi ^{2}})$.
We first note that it is sufficient to show that there exists ![]() $x_0 \in D$ such that
$x_0 \in D$ such that ![]() $\mu (x_0) \in C_{\infty }$. If that is true, then there exists
$\mu (x_0) \in C_{\infty }$. If that is true, then there exists ![]() $n$ such that
$n$ such that ![]() $f^{\circ n'}(x_0) = 0$ and as
$f^{\circ n'}(x_0) = 0$ and as ![]() $f^{\circ n}(\Psi (\phi ^{2}/\Phi (X))) = \Psi (\phi ^{2d}/\Phi ^{d}(X))$ we obtain that the equation
$f^{\circ n}(\Psi (\phi ^{2}/\Phi (X))) = \Psi (\phi ^{2d}/\Phi ^{d}(X))$ we obtain that the equation ![]() $f^{\circ n}(z) = w$ as an analytic solution
$f^{\circ n}(z) = w$ as an analytic solution ![]() $z = g(w)$ satisfying
$z = g(w)$ satisfying ![]() $g(f^{\circ n}(x_0)) = x_0$. This contradicts
$g(f^{\circ n}(x_0)) = x_0$. This contradicts ![]() $f^{\circ n'}(x_0) = 0$.
$f^{\circ n'}(x_0) = 0$.
Now ![]() $\Phi (D)$ contains an open disc
$\Phi (D)$ contains an open disc ![]() $D'$ centred at a point of
$D'$ centred at a point of ![]() $S^{\phi ^{2}}$ and
$S^{\phi ^{2}}$ and ![]() $\phi ^{2}/\Phi (D')$ contains an open set
$\phi ^{2}/\Phi (D')$ contains an open set ![]() $U$ of the form
$U$ of the form ![]() $U = \{r\exp (2\pi i \epsilon ); r_1 < r<1, \epsilon \in I \}$ for some open interval
$U = \{r\exp (2\pi i \epsilon ); r_1 < r<1, \epsilon \in I \}$ for some open interval ![]() $I \subset (0,1)$. It is clear that for
$I \subset (0,1)$. It is clear that for ![]() $n$ large enough the set
$n$ large enough the set ![]() $\{z^{d^{n}}; z \in U\}$ contains an annulus
$\{z^{d^{n}}; z \in U\}$ contains an annulus ![]() $A_0$ of the form
$A_0$ of the form ![]() $A_0 = \{z \in \mathbb {C}; r_1' <|z|< r_2'\}$ for some
$A_0 = \{z \in \mathbb {C}; r_1' <|z|< r_2'\}$ for some ![]() $r_1'< R< r_2'$ and then we can deduce that there exists
$r_1'< R< r_2'$ and then we can deduce that there exists ![]() $z_0 \in U$ such that
$z_0 \in U$ such that ![]() $f^{\circ n}(\Psi (z_0)) = \Psi (z_0^{d^{n}}) = c_0$ with
$f^{\circ n}(\Psi (z_0)) = \Psi (z_0^{d^{n}}) = c_0$ with ![]() $f'(c_0) = 0$. This implies that
$f'(c_0) = 0$. This implies that ![]() $\Psi (z_0) \in C_{\infty }$ and we are finished.
$\Psi (z_0) \in C_{\infty }$ and we are finished.
Now we need an analogue of Lemma 5.6.
Lemma 6.9 Suppose that ![]() $\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty. Then
$\bar {C}_0 \cap ( \partial \mathcal {F}\times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty. Then ![]() $\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is non-empty.
$\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is non-empty.
Proof. Suppose for contradiction that ![]() $\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is empty. As in the proof of Lemma 5.6 we deduce from Lemma 5.1 that
$\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is empty. As in the proof of Lemma 5.6 we deduce from Lemma 5.1 that ![]() $J = \pi _2(\pi _1^{-1}(\Psi (S^{\phi ^{2}}))\cap \bar {C}_0)$ and, in particular, that
$J = \pi _2(\pi _1^{-1}(\Psi (S^{\phi ^{2}}))\cap \bar {C}_0)$ and, in particular, that ![]() $J$ has finitely many connected components. This contradicts the fact that
$J$ has finitely many connected components. This contradicts the fact that ![]() $J$ has infinitely (in fact, uncountably) many connected components.
$J$ has infinitely (in fact, uncountably) many connected components.
Now we prove an analogue of proposition 5.8 and the proof is, in fact, quite similar.
Proposition 6.10 Let ![]() $f$ be, as previously, a polynomial with disconnected Julia set and
$f$ be, as previously, a polynomial with disconnected Julia set and ![]() $P$ be such that there exists
$P$ be such that there exists ![]() $\mathcal {B}$ as in (15). Then there exists
$\mathcal {B}$ as in (15). Then there exists ![]() $\theta \in S^{1}$ such that
$\theta \in S^{1}$ such that ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ for
$P(\Psi (z), \Psi (\theta z)) = 0$ for ![]() $z \in D_R$.
$z \in D_R$.
Proof. We first recall that by Corollary 6.8 ![]() $\bar {C}_0 \cap (\partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty and, thus, also
$\bar {C}_0 \cap (\partial \mathcal {F} \times \mathcal {F}\cup \mathcal {F}\times \partial \mathcal {F})$ is empty and, thus, also ![]() $\bar {C}^{h}_0 \cap (\partial \mathcal {F}^{h} \times \mathcal {F}^{h}\cup \mathcal {F}^{h}\times \partial \mathcal {F}^{h})$ is empty. From Lemma 6.9 follows that
$\bar {C}^{h}_0 \cap (\partial \mathcal {F}^{h} \times \mathcal {F}^{h}\cup \mathcal {F}^{h}\times \partial \mathcal {F}^{h})$ is empty. From Lemma 6.9 follows that ![]() $\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is non-empty. We now prove that
$\bar {C}_0 \cap (\Psi (S^{\phi ^{2}})\times \Psi (S^{\phi ^{2}}) \cup J^{2})$ is non-empty. We now prove that ![]() $\mathcal {C} \cap \Psi (S^{\phi ^{2}})^{2}$ contains an analytic arc. From Lemma 5.2 we deduce that
$\mathcal {C} \cap \Psi (S^{\phi ^{2}})^{2}$ contains an analytic arc. From Lemma 5.2 we deduce that ![]() $\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ or
$\bar {C}_0 \cap \Psi (S^{\phi ^{2}})^{2}$ or ![]() $\bar {C}^{h}_0\cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty. However, those two conditions are equivalent which can be seen by applying complex conjugation and as
$\bar {C}^{h}_0\cap \Psi ^{h}(S^{\phi ^{2}})^{2}$ is non-empty. However, those two conditions are equivalent which can be seen by applying complex conjugation and as ![]() $\Psi (S^{\phi ^{2}})$ is connected we deduce that
$\Psi (S^{\phi ^{2}})$ is connected we deduce that ![]() $\mathcal {C} \cap \Psi (S^{\phi ^{2}})^{2}$ contains infinitely many points and, thus, an analytic arc.
$\mathcal {C} \cap \Psi (S^{\phi ^{2}})^{2}$ contains infinitely many points and, thus, an analytic arc.
We may finish the proof as in the proof of Proposition 5.8.
Now we prove the analogue of Lemma 5.9 for ![]() $f$ with disconnected Julia set.
$f$ with disconnected Julia set.
Lemma 6.11 Let ![]() $f$ be a polynomial with disconnected Julia set and suppose there exists
$f$ be a polynomial with disconnected Julia set and suppose there exists ![]() $\theta \in S^{1}$ and an irreducible polynomial
$\theta \in S^{1}$ and an irreducible polynomial ![]() $P \in \mathbb {C}[X,Y]\setminus \{0\}$ such that
$P \in \mathbb {C}[X,Y]\setminus \{0\}$ such that ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ for
$P(\Psi (z), \Psi (\theta z)) = 0$ for ![]() $z \in D_R$. Then
$z \in D_R$. Then ![]() $\theta \in \mu _\infty$.
$\theta \in \mu _\infty$.
Proof. We first prove that we may assume that there exists ![]() $N \in \mathbb {Z}_{\geq 0}$ such that for all
$N \in \mathbb {Z}_{\geq 0}$ such that for all ![]() $n \geq N$ it holds that if
$n \geq N$ it holds that if ![]() $z \in E_n$, then
$z \in E_n$, then ![]() $\theta z \notin E_n$. Suppose to the contrary that there exist infinitely many
$\theta z \notin E_n$. Suppose to the contrary that there exist infinitely many ![]() $n \in \mathbb {Z}_{\geq 1}$ such that there exists
$n \in \mathbb {Z}_{\geq 1}$ such that there exists ![]() $z \in E_n$ with
$z \in E_n$ with ![]() $\theta z \in E_n$. It follows that
$\theta z \in E_n$. It follows that ![]() $z^{d^{n}}, (\theta z)^{d^{n}} \in \{\Phi (f^{\circ {n_c}}(c)); c \in C_{\text {crit}}\}$ and so
$z^{d^{n}}, (\theta z)^{d^{n}} \in \{\Phi (f^{\circ {n_c}}(c)); c \in C_{\text {crit}}\}$ and so ![]() $\theta ^{d^{n}}$ is contained in a finite set independent of
$\theta ^{d^{n}}$ is contained in a finite set independent of ![]() $n$ for infinitely many
$n$ for infinitely many ![]() $n$. It follows that
$n$. It follows that ![]() $\theta \in \mu _{\infty }$.
$\theta \in \mu _{\infty }$.
We assume now that ![]() $N$ as described previously exists. We can then pick
$N$ as described previously exists. We can then pick ![]() $n$ such that
$n$ such that ![]() $2^{n} > \deg (P)$ and continue the relation
$2^{n} > \deg (P)$ and continue the relation ![]() $P(\Psi (z), \Psi (\theta z)) = 0$ to some
$P(\Psi (z), \Psi (\theta z)) = 0$ to some ![]() $z_0 \in E_n$ such that for the continuation of
$z_0 \in E_n$ such that for the continuation of ![]() $\Psi (z)$ holds
$\Psi (z)$ holds ![]() $\Psi (z_0) \in C_n$. By Lemma 6.1 continuing
$\Psi (z_0) \in C_n$. By Lemma 6.1 continuing ![]() $\Psi (z)$ along a small simple loop around
$\Psi (z)$ along a small simple loop around ![]() $z_0$ sends
$z_0$ sends ![]() $\Psi (z)$ to
$\Psi (z)$ to ![]() $\Psi (\zeta z)$ with
$\Psi (\zeta z)$ with ![]() $\zeta \in \mu _{d^{n}}$ of order at least
$\zeta \in \mu _{d^{n}}$ of order at least ![]() $2^{n}$. Thus, we obtain
$2^{n}$. Thus, we obtain ![]() $P(\Psi (\zeta z), \Psi (\theta z)) = 0$. Now we can continue this relation to
$P(\Psi (\zeta z), \Psi (\theta z)) = 0$. Now we can continue this relation to ![]() $\zeta ^{-1}z_0$ and continue it along a small loop around
$\zeta ^{-1}z_0$ and continue it along a small loop around ![]() $\zeta ^{-1}z_0$. As
$\zeta ^{-1}z_0$. As ![]() $\zeta ^{-1}z_0 \in E_n, \theta \zeta ^{-1}z_0 \notin E_n$ and, thus, we obtain
$\zeta ^{-1}z_0 \in E_n, \theta \zeta ^{-1}z_0 \notin E_n$ and, thus, we obtain ![]() $P(\Psi (\zeta ^{2} z), \Psi (\theta z))= 0$. We can continue this procedure with
$P(\Psi (\zeta ^{2} z), \Psi (\theta z))= 0$. We can continue this procedure with ![]() $\zeta$ replaced by
$\zeta$ replaced by ![]() $\zeta ^{2}$ and then continue inductively to obtain
$\zeta ^{2}$ and then continue inductively to obtain ![]() $P(\Psi (\zeta ^{i} z), \Psi (z)) = 0, i = 0,1,\ldots, 2^{n}-1$. As
$P(\Psi (\zeta ^{i} z), \Psi (z)) = 0, i = 0,1,\ldots, 2^{n}-1$. As ![]() $2^{n} > \deg (\mathcal {C})$ we deduce that
$2^{n} > \deg (\mathcal {C})$ we deduce that ![]() $\partial _X P = 0$ which contradicts the fact that
$\partial _X P = 0$ which contradicts the fact that ![]() $\Psi$ is non-constant.
$\Psi$ is non-constant.
6.3 Proof of Theorem 3 for polynomials with disconnected Julia sets
6.4 Proof of Theorem 4
If ![]() $L_r$ contains a semi-algebraic curve, then so does
$L_r$ contains a semi-algebraic curve, then so does ![]() $f^{\circ n}(L_r)$ and, thus, we may assume that
$f^{\circ n}(L_r)$ and, thus, we may assume that ![]() $L_r \subset D_R$ and that
$L_r \subset D_R$ and that ![]() $L_r = \Psi (S^{\phi })$. Applying complex conjugation and arguing similarly as in the deduction of the relation (15) we deduce that there exists a polynomial
$L_r = \Psi (S^{\phi })$. Applying complex conjugation and arguing similarly as in the deduction of the relation (15) we deduce that there exists a polynomial ![]() $P \in \mathbb {C}[X,Y]\setminus \{0\}$ such that
$P \in \mathbb {C}[X,Y]\setminus \{0\}$ such that ![]() $P(X,\mu (X)) = 0$ identically. Thus, we can continue
$P(X,\mu (X)) = 0$ identically. Thus, we can continue ![]() $\mu$ analytically to a point on
$\mu$ analytically to a point on ![]() $\Psi (S^{\phi ^{2}})$ and deduce from Corollary 5.5 or the proof of Corollary 6.8 that
$\Psi (S^{\phi ^{2}})$ and deduce from Corollary 5.5 or the proof of Corollary 6.8 that ![]() $f$ is exceptional.
$f$ is exceptional.
7. Proof of Theorem 1
We already noted that there exists a place ![]() $v$ of
$v$ of ![]() $K$ such that
$K$ such that ![]() $|f^{\circ n}(\alpha )|_v\rightarrow \infty$ as
$|f^{\circ n}(\alpha )|_v\rightarrow \infty$ as ![]() $n\rightarrow \infty$. We also remarked that the theorem for
$n\rightarrow \infty$. We also remarked that the theorem for ![]() $\alpha$ follows from the theorem for
$\alpha$ follows from the theorem for ![]() $f^{\circ n}(\alpha )$, thus we may assume that
$f^{\circ n}(\alpha )$, thus we may assume that ![]() $\alpha \in \Psi (D_R)$ where
$\alpha \in \Psi (D_R)$ where ![]() $R$ is the convergence radius of
$R$ is the convergence radius of ![]() $z\Psi (z)$ at the place
$z\Psi (z)$ at the place ![]() $v$. If
$v$. If ![]() $v$ is finite, then Theorem 1 follows directly from Proposition 4.1. If, however, the place
$v$ is finite, then Theorem 1 follows directly from Proposition 4.1. If, however, the place ![]() $v$ is infinite, then assuming that the curve
$v$ is infinite, then assuming that the curve ![]() $\mathcal {C}$ has infinite intersection with
$\mathcal {C}$ has infinite intersection with ![]() $\mathcal {S}_\alpha ^{2}$, it also has infinite intersection with
$\mathcal {S}_\alpha ^{2}$, it also has infinite intersection with ![]() $L_r^{2}$ for some
$L_r^{2}$ for some ![]() $r>0$ such that
$r>0$ such that ![]() $L_r\subset \Psi (D_R)$. From Theorem 3 follows that
$L_r\subset \Psi (D_R)$. From Theorem 3 follows that ![]() $\mathcal {C}$ is pre-periodic by
$\mathcal {C}$ is pre-periodic by ![]() $(f,f)$ and Theorem 1 follows from Lemma 2.
$(f,f)$ and Theorem 1 follows from Lemma 2.
8. Proof of Theorem 2
In this section we assume that ![]() $\mathcal {C}$ is not pre-periodic and that it is not fibral and show that
$\mathcal {C}$ is not pre-periodic and that it is not fibral and show that ![]() $\mathcal {C} \cap \mathcal {G}_\alpha$ is finite. With Lemma 2.1 that suffices to conclude Theorem 2. Suppose that
$\mathcal {C} \cap \mathcal {G}_\alpha$ is finite. With Lemma 2.1 that suffices to conclude Theorem 2. Suppose that ![]() $\alpha \in \Psi (D_{v}^{*})$ for some finite place
$\alpha \in \Psi (D_{v}^{*})$ for some finite place ![]() $v$ of
$v$ of ![]() $K$ of good reduction that is co-prime to
$K$ of good reduction that is co-prime to ![]() $d$. For an element
$d$. For an element ![]() $(\beta _1,\beta _2) \in \mathcal {G}_\alpha ^{2} \cap \mathcal {C}(\bar {\mathbb {Q}})$ we set
$(\beta _1,\beta _2) \in \mathcal {G}_\alpha ^{2} \cap \mathcal {C}(\bar {\mathbb {Q}})$ we set ![]() $n_1, m_1, n_2,m_2$ to be the minimal positive integers such that
$n_1, m_1, n_2,m_2$ to be the minimal positive integers such that
The proof goes by bounding ![]() $n_1,n_2,m_1,m_2$ in several steps. In what follows we set
$n_1,n_2,m_1,m_2$ in several steps. In what follows we set
We start by collecting some facts about Kummer extensions.
8.1 Kummer extensions
We first note that as ![]() $|d|_v = 1$, the extension
$|d|_v = 1$, the extension ![]() $K_v(\mu _{d^{\infty }})/K_v$ is an unramified extension [Reference NeukirchNeu92, Satz 7.13]. In particular, the value group of
$K_v(\mu _{d^{\infty }})/K_v$ is an unramified extension [Reference NeukirchNeu92, Satz 7.13]. In particular, the value group of ![]() $K_v(\mu _{d^{\infty }})$ is the same as the value group of
$K_v(\mu _{d^{\infty }})$ is the same as the value group of ![]() $K_v$. It is straightforward to check (for example, by looking at ramification) that for
$K_v$. It is straightforward to check (for example, by looking at ramification) that for ![]() $a \in K_v$ it holds that
$a \in K_v$ it holds that
where the right-hand side is the cardinality of the index as multiplicative groups. We obtain the following immediately.
Lemma 8.1 Let ![]() $K, \alpha, \phi$ be as in the previous sections and
$K, \alpha, \phi$ be as in the previous sections and ![]() $d$ as previously. There exists a constant
$d$ as previously. There exists a constant ![]() $C_{{\rm Kum}} > 0$ depending only on
$C_{{\rm Kum}} > 0$ depending only on ![]() $\alpha, K$ such that
$\alpha, K$ such that
for any integer ![]() $M$ dividing a power of
$M$ dividing a power of ![]() $d$.
$d$.
Proof. As ![]() $\Phi (\alpha ) \in K_v$ and the value group of
$\Phi (\alpha ) \in K_v$ and the value group of ![]() $K_v(\mu _{d^{\infty }})$ is the same as that of
$K_v(\mu _{d^{\infty }})$ is the same as that of ![]() $K_v$, the lemma follows from (20).
$K_v$, the lemma follows from (20).
As a consequence of these observations we obtain the following lemma.
Lemma 8.2 There exists a constant ![]() $C_{{\rm min}} > 0$ such that
$C_{{\rm min}} > 0$ such that ![]() $|{\min \{\ell _1,0\} - \min \{\ell _2,0\}}| \leq C_{\textrm {min}}$.
$|{\min \{\ell _1,0\} - \min \{\ell _2,0\}}| \leq C_{\textrm {min}}$.
Proof. We may assume that ![]() $\ell _1 < \ell _2$ and note that from the above it follows that there is a constant
$\ell _1 < \ell _2$ and note that from the above it follows that there is a constant ![]() $C_{P} > 0$ such that
$C_{P} > 0$ such that ![]() $[K_v(\beta _1, \mu _{d^{\infty }}):K_v(\beta _2, \mu _{d^{\infty }})] \geq C_Pd^{|\!\min \{\ell _1,0\} - \min \{\ell _2,0\}|}$ and as
$[K_v(\beta _1, \mu _{d^{\infty }}):K_v(\beta _2, \mu _{d^{\infty }})] \geq C_Pd^{|\!\min \{\ell _1,0\} - \min \{\ell _2,0\}|}$ and as ![]() $\mathcal {C}$ is not special the claim follows.
$\mathcal {C}$ is not special the claim follows.
8.2 Heights
For the canonical height ![]() $\hat {h}_f$ associated to
$\hat {h}_f$ associated to ![]() $f$, it holds that
$f$, it holds that
We denote by ![]() $d_1,d_2$ the degree of the coordinate functions of
$d_1,d_2$ the degree of the coordinate functions of ![]() $\mathcal {C}$, respectively. By a theorem of Néron the following height inequality holds between the coordinates of a curve.
$\mathcal {C}$, respectively. By a theorem of Néron the following height inequality holds between the coordinates of a curve.
where ![]() $(x,y) \in \mathcal {C}(\bar {\mathbb {Q}})$ and
$(x,y) \in \mathcal {C}(\bar {\mathbb {Q}})$ and ![]() $c = c(\mathcal {C})$ depends only on
$c = c(\mathcal {C})$ depends only on ![]() $\mathcal {C}$.
$\mathcal {C}$.
We can deduce the following lemma quite quickly from the above facts.
Lemma 8.3 There exists a constant ![]() $C_m$ depending only on
$C_m$ depending only on ![]() $\mathcal {C}, \alpha$ such that
$\mathcal {C}, \alpha$ such that ![]() $|\max \{\ell _1, 0\} - \max \{\ell _2, 0\}| \leq C_m$.
$|\max \{\ell _1, 0\} - \max \{\ell _2, 0\}| \leq C_m$.
Proof. There exists a constant ![]() $c_f$ depending only on
$c_f$ depending only on ![]() $f$ such that
$f$ such that ![]() $|h(z) - \hat {h}_f(z)| \leq c_f$ for all
$|h(z) - \hat {h}_f(z)| \leq c_f$ for all ![]() $z \in \bar {\mathbb {Q}}^{*}$. Here
$z \in \bar {\mathbb {Q}}^{*}$. Here ![]() $h$ is the usual logarithmic Weil height. Now combine the equalities (21) and (22) with (23).
$h$ is the usual logarithmic Weil height. Now combine the equalities (21) and (22) with (23).
In the proof of the next lemma we make use of [Reference Ghioca, Nguyen and YeGNY19, Theorem 2.1].
Lemma 8.4 There exists a positive constant ![]() $C_B$ depending only on
$C_B$ depending only on ![]() $\mathcal {C}, \alpha$ such that
$\mathcal {C}, \alpha$ such that ![]() $\max \{\ell _1, \ell _2\} \geq -C_{B}$.
$\max \{\ell _1, \ell _2\} \geq -C_{B}$.
Proof. From [Reference Ghioca, Nguyen and YeGNY19, Theorem 1.5], (21) and (22) it follows that unless ![]() $\mathcal {C}$ is pre-periodic under
$\mathcal {C}$ is pre-periodic under ![]() $(f,f)$, there exists a constant
$(f,f)$, there exists a constant ![]() $c >0$ depending only on
$c >0$ depending only on ![]() $\mathcal {C}$ such that
$\mathcal {C}$ such that ![]() $\hat {h}_f(\beta _1) + \hat {h}_f(\beta _2) \geq c$. From (21) and (22) it follows immediately that
$\hat {h}_f(\beta _1) + \hat {h}_f(\beta _2) \geq c$. From (21) and (22) it follows immediately that ![]() $\max \{m_1 - n_1, m_2-n_2\} \geq -C_{B}$ for some positive constant
$\max \{m_1 - n_1, m_2-n_2\} \geq -C_{B}$ for some positive constant ![]() $C_B$.
$C_B$.
As a corollary of Lemmas 8.2–8.4 we obtain the following.
Corollary 8.5 There exists a constant ![]() $C_{{\rm diff}} > 0$ depending only on
$C_{{\rm diff}} > 0$ depending only on ![]() $\alpha$ and
$\alpha$ and ![]() $\mathcal {C}$ such that for
$\mathcal {C}$ such that for ![]() $\ell _1,\ell _2$ as above, it holds that
$\ell _1,\ell _2$ as above, it holds that
In the following lemma we make use of the uniformity of Proposition 4.1.
Lemma 8.6 For ![]() $n_1$,
$n_1$, ![]() $n_2$,
$n_2$, ![]() $m_1$,
$m_1$, ![]() $m_2$ as in (18) and (19) it holds that
$m_2$ as in (18) and (19) it holds that
for a constant ![]() $C_{{\rm inv}}$ depending only on
$C_{{\rm inv}}$ depending only on ![]() $\alpha$ and
$\alpha$ and ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Let ![]() $M$ be an integer, larger than
$M$ be an integer, larger than ![]() $C_{\text {diff}}$ and consider the finite union of curves
$C_{\text {diff}}$ and consider the finite union of curves
By Proposition 4.1 there exists a constant ![]() $N_{\mathcal {C}}$ such that if
$N_{\mathcal {C}}$ such that if ![]() $(\gamma _1, \gamma _2) \in \tilde {\mathcal {C}}\cap \mathcal {S}_{\beta }^{2}$ for some
$(\gamma _1, \gamma _2) \in \tilde {\mathcal {C}}\cap \mathcal {S}_{\beta }^{2}$ for some ![]() $\beta \in \mathcal {O}_\alpha$, then
$\beta \in \mathcal {O}_\alpha$, then ![]() $f^{N_{\mathcal {C}}}(\gamma _1) = f^{N_{\mathcal {C}}}(\gamma _2) = f^{N_{\mathcal {C}}}(\alpha )$. However, by Corollary 8.5 it holds that if
$f^{N_{\mathcal {C}}}(\gamma _1) = f^{N_{\mathcal {C}}}(\gamma _2) = f^{N_{\mathcal {C}}}(\alpha )$. However, by Corollary 8.5 it holds that if ![]() $(\beta _1,\beta _2) \in \mathcal {C}\cap \mathcal {G}_\alpha ^{2}$, then there exists
$(\beta _1,\beta _2) \in \mathcal {C}\cap \mathcal {G}_\alpha ^{2}$, then there exists ![]() $\tilde {\mathcal {C}} \in S_{\mathcal {C}}$ such that
$\tilde {\mathcal {C}} \in S_{\mathcal {C}}$ such that ![]() $(f^{k_1}(\beta _1), f^{k_2}(\beta _2)) \in \tilde {\mathcal {C}}\cap \mathcal {S}_\beta ^{2}$ for some
$(f^{k_1}(\beta _1), f^{k_2}(\beta _2)) \in \tilde {\mathcal {C}}\cap \mathcal {S}_\beta ^{2}$ for some ![]() $\beta \in \mathcal {O}_\alpha$ and
$\beta \in \mathcal {O}_\alpha$ and ![]() $0\leq k_1,k_2 \leq M+ C_{\text {diff}}$. This concludes the proof of the lemma.
$0\leq k_1,k_2 \leq M+ C_{\text {diff}}$. This concludes the proof of the lemma.
8.3 Concluding the proof
From Lemma 8.6 and Corollary 8.5 it follows that
where
(In fact, it is enough to consider the curves for which ![]() $f_1 = 0$ or
$f_1 = 0$ or ![]() $f_2 = 0$). Now if the left-hand side is infinite, then the intersection of two curves in the union of curves
$f_2 = 0$). Now if the left-hand side is infinite, then the intersection of two curves in the union of curves ![]() $(f^{-\circ n_1},f^{-\circ n_2})(\mathcal {C}) \cap S_{f_1,f_2}$ contains a one-dimensional component. It follows that there exist
$(f^{-\circ n_1},f^{-\circ n_2})(\mathcal {C}) \cap S_{f_1,f_2}$ contains a one-dimensional component. It follows that there exist ![]() $n,m$ such that
$n,m$ such that ![]() $f^{\circ n}(\xi ) = f^{\circ m}(\eta )$ for the coordinate functions
$f^{\circ n}(\xi ) = f^{\circ m}(\eta )$ for the coordinate functions ![]() $\xi, \eta$ of
$\xi, \eta$ of ![]() $\mathcal {C}$, which contradicts our assumption on
$\mathcal {C}$, which contradicts our assumption on ![]() $\mathcal {C}$ not being pre-periodic.
$\mathcal {C}$ not being pre-periodic.
9. Concluding remarks
In this section we discuss some issues surrounding effectivity and uniformity as well as future work.
It seems feasible to obtain an entirely effective version of Theorem 1. The main issue seems to be making Proposition 4.1 effective. Almost all steps in the proof of Proposition 4.1 can be made effective quite straightforwardly, but in the case of Lemma 4.11 especially more work is required as its proof uses something akin to a compactness argument.
In order to make Theorem 3 effective, we can employ some sort of effective implicit function theorem such as in [Reference LangLan73, p. 124] and estimate the partial derivatives of the function ![]() $P(\Psi (z), \Psi (w))$ carefully which seems to be feasible to be done effectively.
$P(\Psi (z), \Psi (w))$ carefully which seems to be feasible to be done effectively.
A stumbling block on the way to effectivity for Theorem 2 is that we use the results on the dynamical Bogomolov conjecture by Ghioca, Nguyen and Ye. However, if the degree ![]() $d$ is prime, there is some hope that the methods in this paper might suffice.
$d$ is prime, there is some hope that the methods in this paper might suffice.
For our final theorem, we use ![]() $o$-minimality (perhaps some weaker machinery would suffice) to find a uniform version of Theorem 3.
$o$-minimality (perhaps some weaker machinery would suffice) to find a uniform version of Theorem 3.
Theorem 10 There exists a constant ![]() $C_D$ depending only on
$C_D$ depending only on ![]() $D$ such that any curve of total degree at most
$D$ such that any curve of total degree at most ![]() $D$ satisfies
$D$ satisfies
for ![]() $\exp (-r)< R/2$ unless
$\exp (-r)< R/2$ unless ![]() $\mathcal {C}$ has the form in the conclusion of Theorem 3.
$\mathcal {C}$ has the form in the conclusion of Theorem 3.
Proof. The complex-analytic function ![]() $\Psi (z)$ is definable in the structure
$\Psi (z)$ is definable in the structure ![]() $\mathbb {R}_{an}$ on the open disc of radius
$\mathbb {R}_{an}$ on the open disc of radius ![]() $R/2$ and the statement follows from standard properties of
$R/2$ and the statement follows from standard properties of ![]() $o$-minimal structures because the sets
$o$-minimal structures because the sets
as ![]() $P$ varies over polynomials of degree at most
$P$ varies over polynomials of degree at most ![]() $D$ and
$D$ and ![]() $\phi$ in the interval
$\phi$ in the interval ![]() $(0,R/2)$ form a definable family. There is a uniform bound on the number of connected components of the members of a definable family in
$(0,R/2)$ form a definable family. There is a uniform bound on the number of connected components of the members of a definable family in ![]() $\mathbb {R}_{an}$ (see [Reference van den DriesvdDri98]) and we deduce the present theorem from Theorem 3.
$\mathbb {R}_{an}$ (see [Reference van den DriesvdDri98]) and we deduce the present theorem from Theorem 3.
Theorem 10 implies that we have a similar uniformity in orbits as in Proposition 4.1. However, we are missing the strong Galois bounds or, in fact, any arithmetic Galois information in order to extend Theorem 2 to infinite places. This is an interesting direction for future research.
We can prove variations of Theorem 1 in that we can mix our statement with the dynamical Bogomolov conjecture. For example, our methods seem to allow structure theorems to be proved for ![]() $\mathcal {S}_\alpha \times \text {Preper}$ (perhaps under some conditions on
$\mathcal {S}_\alpha \times \text {Preper}$ (perhaps under some conditions on ![]() $\alpha$) where
$\alpha$) where ![]() $\text {Preper}$ is the set of pre-periodic points. This will be explored in a future paper.
$\text {Preper}$ is the set of pre-periodic points. This will be explored in a future paper.
We now show that an extension of Theorem 2 to pre-periodic ![]() $\alpha$ is not possible. For this let
$\alpha$ is not possible. For this let ![]() $g$ be a polynomial of degree 2 defined over the reals, whose Julia set is connected and let
$g$ be a polynomial of degree 2 defined over the reals, whose Julia set is connected and let ![]() $f = g^{\circ 3}$. Then every periodic external ray of
$f = g^{\circ 3}$. Then every periodic external ray of ![]() $f$ lands [Reference MilnorMil06, Theorem 18.1]. Note that
$f$ lands [Reference MilnorMil06, Theorem 18.1]. Note that ![]() $\Psi (z^{2}) = g(\Psi (z))$. Let
$\Psi (z^{2}) = g(\Psi (z))$. Let ![]() $\zeta _3$ be primitive third root of unity and let
$\zeta _3$ be primitive third root of unity and let
We set ![]() $\alpha$ to be the limit point of
$\alpha$ to be the limit point of ![]() $E$ as
$E$ as ![]() $r \rightarrow 1$. Then
$r \rightarrow 1$. Then ![]() $f^{\circ 2}(\alpha ) = \alpha$ as
$f^{\circ 2}(\alpha ) = \alpha$ as ![]() $f^{\circ 2}(E) = E$ and for
$f^{\circ 2}(E) = E$ and for
it holds that ![]() $|\mathcal {C}\cap \mathcal {G}_\alpha ^{2}| = \infty$. To see this, we can consider
$|\mathcal {C}\cap \mathcal {G}_\alpha ^{2}| = \infty$. To see this, we can consider ![]() $\alpha _n$ the limiting point of
$\alpha _n$ the limiting point of ![]() $E_n = \{\Psi (r\zeta ); r \in (1,\infty )\}$ where
$E_n = \{\Psi (r\zeta ); r \in (1,\infty )\}$ where ![]() $\zeta = \zeta _{8^{n}}\zeta _3$ for a primitive
$\zeta = \zeta _{8^{n}}\zeta _3$ for a primitive ![]() $8^{n}$th root of 1,
$8^{n}$th root of 1, ![]() $\zeta _{8^{n}}$. Then
$\zeta _{8^{n}}$. Then ![]() $f^{\circ n}(E_n) = f^{\circ n}(E)$ and, thus,
$f^{\circ n}(E_n) = f^{\circ n}(E)$ and, thus, ![]() $f^{\circ n}(\alpha _n) = f^{\circ n}(\alpha )$. However, it also holds that
$f^{\circ n}(\alpha _n) = f^{\circ n}(\alpha )$. However, it also holds that ![]() $f^{\circ 2n +1}(g(E_n)) = E_n$ and, thus,
$f^{\circ 2n +1}(g(E_n)) = E_n$ and, thus, ![]() $(\alpha _n ,g(\alpha _n)) \in \mathcal {G}_\alpha ^{2}$ for all
$(\alpha _n ,g(\alpha _n)) \in \mathcal {G}_\alpha ^{2}$ for all ![]() $n \geq 1$. Moreover, the set of
$n \geq 1$. Moreover, the set of ![]() $\alpha _n$ just constructed is infinite [Reference MilnorMil06, Lemma 18.3].
$\alpha _n$ just constructed is infinite [Reference MilnorMil06, Lemma 18.3].
However, the variety ![]() $\mathcal {C}$ is not in the zero locus of
$\mathcal {C}$ is not in the zero locus of ![]() $f^{\circ n}(X)- f^{\circ m}(Y)$ for any choice of non-zero integers
$f^{\circ n}(X)- f^{\circ m}(Y)$ for any choice of non-zero integers ![]() $n,m$ and, thus, we cannot extend Theorem 2 to pre-periodic points.
$n,m$ and, thus, we cannot extend Theorem 2 to pre-periodic points.
9.1 A conjecture for grand orbits
In this subsection we want to generalise Conjecture 1 to all projective varieties, following a suggestion of Ghioca. It is modelled after the conjecture of Ghioca and Tucker on pre-periodic varieties [Reference Ghioca and TuckerGT21]. The novelty is that we need to define an analogue of a co-set for dynamical systems.
We assume that everything is defined over some algebraically closed field ![]() $\mathcal {K}$ of charact- eristic zero. We let
$\mathcal {K}$ of charact- eristic zero. We let ![]() $\mathcal {X}$ be a projective variety and let
$\mathcal {X}$ be a projective variety and let ![]() $f: \mathcal {X} \rightarrow \mathcal {X}$ be an endomorphism of degree at least 2. We first give a definition of admissible tuple associated to
$f: \mathcal {X} \rightarrow \mathcal {X}$ be an endomorphism of degree at least 2. We first give a definition of admissible tuple associated to ![]() $f, \mathcal {X}$.
$f, \mathcal {X}$.
Definition 3 Let ![]() $\mathcal {V} \subset \mathcal {X}$ be a subvariety. A tuple
$\mathcal {V} \subset \mathcal {X}$ be a subvariety. A tuple ![]() $(\mathcal {Y}, h, H,\tilde {\mathcal {V}}, \varphi )$ is admissible for
$(\mathcal {Y}, h, H,\tilde {\mathcal {V}}, \varphi )$ is admissible for ![]() $(\mathcal {X}, f, \mathcal {V})$ if the following holds. First,
$(\mathcal {X}, f, \mathcal {V})$ if the following holds. First, ![]() $\mathcal {Y}$ is a projective variety and
$\mathcal {Y}$ is a projective variety and ![]() $h, H$ are endomorphism of
$h, H$ are endomorphism of ![]() $\mathcal {Y}$ of degree at least 2 that commute. Moreover,
$\mathcal {Y}$ of degree at least 2 that commute. Moreover, ![]() $\varphi$ is a rational map
$\varphi$ is a rational map ![]() $\varphi : \mathcal {Y} \rightarrow \mathcal {X}$ with finite fibres that satisfies
$\varphi : \mathcal {Y} \rightarrow \mathcal {X}$ with finite fibres that satisfies ![]() $\varphi \circ f^{\circ n} = h\circ \varphi$ for some
$\varphi \circ f^{\circ n} = h\circ \varphi$ for some ![]() $n \geq 0$, as well as
$n \geq 0$, as well as ![]() $\varphi (\tilde {\mathcal {V}}) = \mathcal {V}$.
$\varphi (\tilde {\mathcal {V}}) = \mathcal {V}$.
Note that we can take ![]() $\mathcal {Y} = \mathcal {Y}$ and
$\mathcal {Y} = \mathcal {Y}$ and ![]() $H=h = f, \tilde {\mathcal {V}} = \mathcal {V}$ as well as
$H=h = f, \tilde {\mathcal {V}} = \mathcal {V}$ as well as ![]() $\varphi$ to be the identity to obtain an admissible tuple. Now we can define a notion of a variety to be dynamically weakly special with respect to
$\varphi$ to be the identity to obtain an admissible tuple. Now we can define a notion of a variety to be dynamically weakly special with respect to ![]() $f$.
$f$.
Definition 4 We say that a subvariety ![]() $\mathcal {V}\subset \mathcal {X}$ is dynamically weakly special with respect to
$\mathcal {V}\subset \mathcal {X}$ is dynamically weakly special with respect to ![]() $f$ if there exists an admissible tuple
$f$ if there exists an admissible tuple ![]() $(\mathcal {Y}, h, H,\tilde {\mathcal {V}}, \varphi )$ for
$(\mathcal {Y}, h, H,\tilde {\mathcal {V}}, \varphi )$ for ![]() $(\mathcal {X}, f, \mathcal {V})$ such that either
$(\mathcal {X}, f, \mathcal {V})$ such that either ![]() $\tilde {\mathcal {V}}$ is pre-periodic by
$\tilde {\mathcal {V}}$ is pre-periodic by ![]() $H$ or
$H$ or ![]() $\mathcal {Y} = \mathcal {Y}_1 \times \mathcal {Y}_2$ (with
$\mathcal {Y} = \mathcal {Y}_1 \times \mathcal {Y}_2$ (with ![]() $\dim (\mathcal {Y}_2) > 0$) and
$\dim (\mathcal {Y}_2) > 0$) and ![]() $H(\tilde {\mathcal {V}}) \subset \mathcal {Y}_1\times \{\alpha \}$ for some
$H(\tilde {\mathcal {V}}) \subset \mathcal {Y}_1\times \{\alpha \}$ for some ![]() $\alpha \in \mathcal {Y}_2(\mathcal {K})$.
$\alpha \in \mathcal {Y}_2(\mathcal {K})$.
As in the introduction we define the grand orbit of a point ![]() $\alpha \in \mathcal {X}(\mathcal {K})$ by an endomorphism
$\alpha \in \mathcal {X}(\mathcal {K})$ by an endomorphism ![]() $f$ to be
$f$ to be
Now let ![]() $\mathcal {X}_1, \ldots, \mathcal {X}_n$ be projective varieties and let
$\mathcal {X}_1, \ldots, \mathcal {X}_n$ be projective varieties and let ![]() $f_1, \ldots, f_n$ be endomorphisms of
$f_1, \ldots, f_n$ be endomorphisms of ![]() $\mathcal {X}_1, \ldots, \mathcal {X}_n$, respectively, such that
$\mathcal {X}_1, \ldots, \mathcal {X}_n$, respectively, such that ![]() $f = (f_1, \ldots, f_n)$ has degree at least 2.
$f = (f_1, \ldots, f_n)$ has degree at least 2.
Conjecture 2 Let ![]() $\mathcal {X} = \mathcal {X}_1 \times \cdots \times \mathcal {X}_n$ and
$\mathcal {X} = \mathcal {X}_1 \times \cdots \times \mathcal {X}_n$ and ![]() $(\alpha _1, \ldots, \alpha _n) \in \mathcal {X}(\mathcal {K})$. If for an irreducible subvariety
$(\alpha _1, \ldots, \alpha _n) \in \mathcal {X}(\mathcal {K})$. If for an irreducible subvariety ![]() $\mathcal {V} \subset \mathcal {X}$ it holds that
$\mathcal {V} \subset \mathcal {X}$ it holds that
is infinite, then ![]() $\mathcal {V}$ is dynamically weakly special with respect to
$\mathcal {V}$ is dynamically weakly special with respect to ![]() $f$.
$f$.
If all points ![]() $\alpha _1, \ldots, \alpha _n$ are pre-periodic, then Conjecture 2 follows from Conjecture 1.2 in [Reference Ghioca and TuckerGT21] as we can take (in the notation there)
$\alpha _1, \ldots, \alpha _n$ are pre-periodic, then Conjecture 2 follows from Conjecture 1.2 in [Reference Ghioca and TuckerGT21] as we can take (in the notation there) ![]() $\mathcal {X} = X$,
$\mathcal {X} = X$, ![]() $\mathcal {V} = Z$ as well as
$\mathcal {V} = Z$ as well as ![]() $(Y, \Phi _{|Y},\Psi, i )$ as an admissible tuple where
$(Y, \Phi _{|Y},\Psi, i )$ as an admissible tuple where ![]() $i$ is the inclusion of
$i$ is the inclusion of ![]() $Y$ in
$Y$ in ![]() $X$.
$X$.
Acknowledgements
Special thanks goes to Myrto Mavraki for answering a lot of questions about the arithmetic of dynamical systems and for reading a previous draft of this paper. Thanks also go to Holly Krieger for answering my first basic questions about the state of the art of the arithmetic of dynamical systems. It is also a great pleasure to thank my colleagues at Universität Basel (some of them not there anymore) Gabriel Dill, Richard Griffon, Philipp Habegger, Lars Kühne, Myrto Mawraki, Julia Schneider and Robert Wilms for many discussions surrounding this paper. A big thanks goes to Laura Demarco and to Dragos Ghioca for valuable advice and encouragement as well as helpful comments. Another big thanks goes to Federico Pellarin for answering questions about Mahler functions. Finally, I would like to heartily thank Philipp Habegger and the mathematical department of Basel (and its staff) for continuing support on all fronts. I would also like to thank the referee for his careful reading and many helpful suggestions which have greatly improved the exposition.