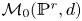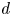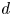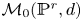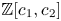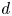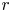1. Introduction
1.1 Results and strategy of proof
The main goal of this work is to compute the integral Chow ring of the interior of the space of stable maps of odd degree from rational curves to projective space; its closed points parameterize maps from irreducible source curves isomorphic to 
$\mathbb {P}^1$. We exhibit this ring as the quotient of a polynomial ring in two variables, and provide an efficient set of generators for the ideal of relations. We state here the complete result, which is proven in several steps throughout the paper.
Main Theorem (Theorems 3.8, 4.3, 5.1 and 6.1)
For 
$r$ a positive integer and 
$d$ an odd positive integer, a presentation for the integral Chow ring of the stack 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$ is given by
\[ A^\ast(\mathcal{M}_{0}(\mathbb{P}^r, d)) = \frac{\mathbb{Z}[c_1,c_2]}{(\alpha^{r,d}_{i,k})_{i,k}}, \]
where 
$c_i$ is a graded variable of degree 
$i$ and 
$\alpha _{i,k}^{r,d}$ is homogeneous of degree 
$ir+k$ (Theorem 3.8). In order to generate the ideal of relations it is sufficient to consider the following values for 
$i,k$ (Theorem 4.3):
•
$i = 1$ and $k = 0,1$;•
$i$ is a prime power and $k = 0$.
The generating relations are exhibited in generating function form, where
\[ \mathcal{A}_{i,k}(d) := \sum_{r=0}^{\infty} \alpha_{i,k}^{r,d}. \]
Relations of the form 
$\alpha ^{r,d}_{1,k}$ are computed explicitly in Theorem 5.1:
\begin{align*} \mathcal{A}_{1,0}(d) &= \frac{d}{\bigl(1+(({d-1})/{2})c_1\bigr)\bigl(1-(({d+1})/{2})c_1\bigr)+d^2c_2},\\ \mathcal{A}_{1,1}(d) &= \frac{1+(({d-1})/{2})c_1}{\bigl(1+(({d-1})/{2})c_1\bigr)\bigl(1-(({d+1})/{2})c_1\bigr)+d^2c_2}-1. \end{align*}
Relations of the form 
$\alpha ^{r,d}_{i,0}$ are computed in Theorem 6.1 as
\[ \mathcal{A}_{i,0}(d)= \sum_{j=0}^{i}
\frac{(-1)^{j}}{i! (l_1-l_2)^i}\binom{i}{j}\biggl[\biggl(1-\frac{\prod_{k = 0}^{d}\bigl({c_1}/{2}+(k-{d}/{2})(l_1-l_2)
\bigr)}{\prod_{k = j}^{d-i+j}\bigl({c_1}/{2}+(k-{d}/{2})(l_1-l_2)\bigr)}\biggr)^{-1}-1\biggr],\]
where 
$-l_1, -l_2$ are the Chern roots of the variables 
$c_1, c_2$, i.e. 
$c_1 = -l_1-l_2$ and 
$c_2 = l_1l_2$.
The integral Chow rings of the spaces 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$ exhibit a remarkable combinatorial structure. In Corollary 6.5 it is shown that for fixed 
$i,r$, the relations of the form 
$\alpha _{i,0}$ are polynomial in 
$d$, whereas in Corollary 6.4 one sees that, for fixed 
$d,r$, all relations of the form 
$\alpha _{i,0}$ may be extracted from a single two-variable monomial via the action of a differential operator, and an appropriate Hadamard product of multi-variate power series.
The proof of the main theorem is organized into three main stages: the first consists of producing a presentation of 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$, where the ideal of relations has a very redundant generating set; the second consists of eliminating a large number of redundant generators; and in the third we compute the remaining relations.
To obtain a presentation of 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$, we exhibit 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$ as a global quotient stack 
$[\widehat {U}_{r,d}/\text { GL}_2]$ of an open set in affine space by the action of the group 
$\text { GL}_2$, thus reducing the task to computing the 
$\text { GL}_2$ equivariant Chow ring of 
$\widehat {U}_{r,d}$. It is at this moment that the hypothesis of 
$d$ being odd becomes necessary. By considering 
$\widehat {U}_{r,d}$ as a 
$\mathbb {G}_m$-bundle over its image in projective space, we reduce the computation of the equivariant Chow ring of 
$\widehat {U}_{r,d}$ to that of its image 
$U_{r,d}$: this is an open set in projective space, and its complement is covered by a 
$\text { GL}_2$-equivariant envelope 
$\bigsqcup _i \{\widetilde {Z}_i \stackrel {\pi _i}{\longrightarrow } \mathbb {P}^N \}$. Its connected components 
$\widetilde {Z}_i\cong \mathbb {P}^i\times \mathbb {P}^{N_i}$ are isomorphic to products of projective spaces. Using the standard excision sequence, we exhibit the Chow ring of 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$ as the quotient of the Chow ring of the ambient projective space by the ideal generated by the images of the push-forward maps from the components of the envelope.
Elementary arguments suffice to show that the push-forward 
${\pi _{i}}_\ast (h_i^k)$ of powers of the hyperplane classes from the left factor of the 
$Z_i$, with degree bounded by 
$i$, generate the ideal of relations. In order to further reduce the set of necessary generators, a more subtle analysis is needed. One may replace the powers 
$h_i^k$ in the 
$i$th component of the envelope with suitably chosen monic polynomials in 
$h_i$. In many cases, such polynomials may be seen as arising from classes from lower envelopes, leading to an inductive argument that allows to narrow down the indispensable generators to those mentioned in the main theorem. The generating set we obtain is still not minimal, as can be seen from the computations in § 7.2. Experimental computations led to the following conjecture.
Conjecture 7.2 Consider the presentation of 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$ from Theorem 3.8. A minimal set of generators for the ideal of relations is given by 
$\alpha _{1,0}^{r,d}, \alpha _{1,1}^{r,d}$ and 
$\alpha _{p,0}^{r,d}$ where 
$p$ runs over all primes that divide 
$d$.
Regardless of the optimal generating set, we set forth to compute all relations coming from the first component of the envelope or from the push-forward of fundamental classes of any other component of the envelope. We use two different techniques to compute the two types of relations. For the relations coming from the first envelope, the embedding of 
$\mathbb {P}^r$ as a coordinate hyperplane in 
$\mathbb {P}^{r+1}$ gives the relations a recursive structure which allows to reconstruct them for all values of 
$r$ from the degenerate 
$r=0$ case. Encoding the relations in generating function form, the recursions become a linear system of functional equations which is easily solved. Such recursive structure is present for the relations coming from higher envelopes, but it becomes substantially more computationally intensive to use this technique to extract the relations. Hence, for the fundamental class relations, we instead use the Atyiah–Bott localization theorem on the left factor of the envelope 
$Z_i$ to obtain an expression for the fundamental class supported at the fixed points. Such an expression is then readily pushed forward to obtain the formulas in the main theorem.Footnote 1 The drawback of this technique is that the answer is not produced immediately as a polynomial in 
$c_1, c_2$, but rather as a (non-obviously) symmetric polynomial in the Chern roots 
$l_1, l_2$. It would be interesting to symmetrize formula (43).
1.2 History, motivation and considerations
One of the key conceptual leaps in modern enumerative geometry has been the translation of enumerative questions into intersection theory on appropriate moduli spaces of geometric objects. Thus, for example, the unique conic through five points in the plane is obtained as the intersection of 5 hyperplanes in the 
$\mathbb {P}^5$ of all conics and 12 rational cubics through 8 points arise as the intersection of 8 hyperplanes and the discriminant hypersurface in the 
$\mathbb {P}^9$ of plane cubics.
The rich and rapid development of the field that followed in the late 1800s led to many exciting computations, some of which were alas incorrect; these early mistakes brought awareness of many delicate issues and technical difficulties in implementing the intuitive plan of counting geometric objects by intersecting subvarieties in moduli spaces. On the one hand, this led to Hilbert's 15th problem [Reference HilbertHil30], requesting rigorous foundations for Schubert calculus, which we now understand as intersection theory on Grassmannians and flag varieties. On the other, new perspectives on geometric objects and their moduli were developed to tackle even the most classical problems. For example, the classical enumerative problem of counting the number of plane rational curves of degree 
$d$ through 
$3d-1$ general points was solved in [Reference KontsevichKon95] by introducing the moduli spaces of stable maps, that shifted the perspective by thinking of plane curves as the images of functions from abstract curves.
The main object of study in algebraic intersection theory [Reference FultonFul98, Reference Eisenbud and HarrisEH16] is the Chow ring, a codimension-graded ring generated by equivalence classes of closed subvarieties up to rational equivalence, where the product extends the notion of transverse intersection of subvarieties. A full understanding of the Chow ring of a moduli space gives access, in principle, to any enumerative geometric problem involving the geometric objects described by the moduli space. It should come as no surprise then that Chow rings of moduli spaces are typically very sophisticated and hard to compute objects. To further complicate things, automorphisms of geometric objects cause most moduli spaces to be represented only by stacks, rather than varieties or schemes.
Working with rational coefficients gives the significant advantage that the Chow ring of a Deligne–Mumford stack agrees with that of its coarse moduli space, see [Reference EdidinEdi13, Theorem 4.40]. Still, the Chow ring of moduli spaces of curves 
$\mathcal {M}_g$ are known only up to 
$g = 9$ [Reference MumfordMum83, Reference FaberFab90a, Reference FaberFab90b, Reference IzadiIza95, Reference Penev and VakilPV15, Reference Canning and LarsonCL21] and for 
$\overline {\mathcal {M}}_g$ up to 
$g = 3$ [Reference MumfordMum83, Reference FaberFab90a]. In recent work [Reference Canning and LarsonCL22] it was shown that for genus up to seven the rational coefficients Chow rings of 
$\overline {\mathcal {M}}_g$ are tautological, and therefore algorithmically computable.
Although rational coefficients are often sufficient for any application to enumerative problems, they cause to lose all torsion classes, arguably containing interesting information about the geometry of the moduli space. For example, the stack of smooth hyperelliptic curves of genus 
$g$ has coarse moduli space which is a finite quotient of 
$M_{0,2g+2}$ (an open subset of 
$\mathbb {A}^{2g-1})$, and has therefore trivial Chow ring, i.e. 
$A^\ast (\mathcal {H}_g, \mathbb {Q}) = \mathbb {Q}$.
Edidin and Graham [Reference Edidin and GrahamEG98a] generalized the work of Totaro [Reference TotaroTot99] and approached the study of Chow rings of moduli spaces with integer coefficients via equivariant geometry: if a moduli space is presented as a global stack quotient 
$[X/G]$, then its integral Chow ring is the equivariant Chow ring 
$A^\ast _G(X).$
This perspective was used to unveil rich torsion structure in the integral Chow ring of hyperelliptic loci [Reference Edidin and FulghesuEF09, Reference Di LorenzoDL21], and in the locus of non-hyperelliptic curves of genus three [Reference Di Lorenzo, Fulghesu and VistoliDLFV21]. The only moduli spaces of curves for which the integral Chow ring has been computed are 
$\overline {\mathcal {M}}_{2}$ (see [Reference LarsonLar21a]) and 
$\overline {\mathcal {M}}_{2,1}$ (see [Reference Di Lorenzo, Pernice and VistoliDLPV21]).
Besides hyperelliptic loci, there are few infinite families of moduli spaces for which the integral Chow ring is known, with the list substantially grown thanks to notable recent work [Reference LarsonLar21b, Reference CanningCan21, Reference Canning, di Lorenzo and InchiostroCdLI22]. The most classical case is that of Grassmannians 
$G(k,n)$. A structurally satisfying presentation for the Chow rings of Grassmannians is given, for example, in [Reference Eisenbud and HarrisEH16, Theorem 5.26]: 
$A^{\ast }(G(k,r+1), \mathbb {Z})$ is a quotient of the polynomial ring 
$\mathbb {Z}[c_1, \ldots, c_k]$, where 
$c_i$ is a variable of degree 
$i$. The ideal of relations is generated by the homogeneous terms of degrees between 
$r+2-k$ and 
$r+1$ in the power series expansion ofFootnote 2
\begin{equation} \frac{1}{1-c_1+c_2-\cdots +(-1)^k c_k}. \end{equation}
We view (1) as a generating function for the ideal of relations of all Grassmannians of 
$k$ planes as the ambient dimension 
$r+1$ varies.
When 
$k=2$, we have 
$Gr(2,r+1) \cong \mathcal {M}_{0}(\mathbb {P}^r, 1)$, and it is easily seen that the terms of degree 
$r$ and 
$r+1$ of 
$1/(1-c_1+c_2)$ agree with the generating functions 
$\mathcal {A}_{1,0}(1)$ and 
$\mathcal {A}_{1,1}(1)$ from the main theorem.
In [Reference PandharipandePan98], Pandharipande considered the function 
$\Phi _f: Gr(2,r+1) = \mathcal {M}_{0}(\mathbb {P}^r, 1)\to \mathcal {M}_{0}(\mathbb {P}^r, d)$ induced by post-composition with a fixed degree 
$d$ map 
$f:\mathbb {P}^r\to \mathbb {P}^r$. He showed that when working with rational coefficients, the pull-back
\begin{equation} \Phi_f^\ast: A^\ast(\mathcal{M}_{0}(\mathbb{P}^r, d),\mathbb{Q})\to A^\ast(\mathcal{M}_{0}(\mathbb{P}^r, 1),\mathbb{Q}) \end{equation}
is an isomorphism. It is interesting to observe how this result relates to the main theorem. First off, all relations 
$\alpha _{i,0}$ with 
$i>1$ are 
$i$-torsion and, therefore, vanish when tensoring coefficients with 
$\mathbb {Q}$. In order to check that relations from the first envelope agree, one must analyze the lift
\[ \widehat{\Phi}_f: \widehat U_{r,1}\to \widehat U_{r,d}, \]
where the 
$\text { GL}_2$-action on the two spaces is as in Proposition 2.4. A non-trivial endomorphism 
$\varphi _f$ of 
$\text { GL}_2$ is required to make the map 
$\widehat {\Phi }_f$ equivariant and this induces the transformation 
$\varphi _f^\ast (c_1) = {c_1}/{d}$, 
$\varphi _f^\ast (c_2) = c_2 -{(d^2-1)c_1^2}/{4d^2}$. It is then immediate to check that the relations agree up to global factors which are powers of 
$d$ (irrelevant after tensoring with 
$\mathbb {Q})$. The result in [Reference PandharipandePan98] is, in fact, more general, asserting that the rational coefficients Chow rings of spaces of degree 
$d$ maps from 
$\mathbb {P}^k$ to 
$\mathbb {P}^r$ are independent of 
$d$. It is reasonable to expect that a similar comparison statement for the integral coefficients Chow rings would hold in the case 
$k>1$.
We make two important assumptions on the base field 
$k$. The first is that 
$k$ is algebraically closed. We use this condition to unambiguously determine the degree of certain maps in Lemma 4.2. Moreover, we assume that the base field has characteristic zero or greater than 
$d$. This condition allows us to work with localization formulas and to construct formula (49).
1.3 Notation
There are four main discrete invariants that take different values in this work:
(i)
$r$, the dimension of the target projective space;(ii)
$d$, the degree of the map $f:\mathbb {P}^1\to \mathbb {P}^r$ or equivalently of the $(r+1)$ defining polynomials;(iii)
$i$, the component of the envelope parameterizing polynomials that contain a common factor of degree $i$;(iv)
$k$, the power of the hyperplane class on the left factor of $\mathbb {P}(W_i)\times \mathbb {P}(W_{d-i}^{\oplus r+1})$.
As a consequence, the generators of the ideal of relations for the presentation of 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$ are polynomials 
$\alpha _{i,k}^{r,d}$ depending on four indices.
Convention 1.1 To lighten this notation, we adopt the convention of suppressing indices corresponding to discrete invariants that remain fixed throughout a section. Thus, for example, in § 3, where 
$r$ and 
$d$ are fixed, the relations are denoted 
$\alpha _{i,k}$; whereas in §§ 5, where we consider maps comparing different 
$\mathbb {P}^r$, we maintain the superscript 
$r$. A similar convention is adopted for any other quantity depending on these four discrete invariants.
The Chow ring 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$ is presented as a quotient of the equivariant Chow ring of 
$\mathbb {P}(W_{d}^{\oplus r+1})$, where one of the relations is 
$H - (d+1)c_1/2$. One may then eliminate the hyperplane class 
$H$ and regard 
$A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$ as a quotient of the polynomial ring 
$\mathbb {Z}[c_1, c_2]$. We adopt the following notation to deal with this phenomenon.
Convention 1.2 We denote the class 
$\pi _{i_\ast }(h_i^k)$ by 
$\alpha _{i,k}(H)$ when we wish to regard it as a Chow class on 
$\mathbb {P}(W_{d}^{\oplus r+1})$, by 
$\alpha _{i,k}$ when we wish to regard it as a Chow class on 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$, so that 
$\alpha _{i, k}=\alpha _{i,k}((d+1)c_1/2)$. This convention extends to any other class with such double personality.
Some of the commonly recurring notation throughout the paper is collected in Table 1.
Table 1. Recurring notation.
2. Presentation of the stack $\mathcal {M}_{0}(\mathbb {P}^r, 2s+1)$
Let 
$k$ be an algebraically closed field of characteristic zero or larger than 
$2s+1$. We refer the reader to [Reference Fulton and PandharipandeFP97] for a general definition of the stack of stable maps 
$\mathcal {M}_{g,n}(X,\beta )$ where 
$X$ is a projective variety and 
$\beta$ is a class in 
$A_1(X,\mathbb {Z})$. In this paper, we focus on the special case 
$\mathcal {M}_{0}(\mathbb {P}^r,d)$ of maps from rational curves to projective space. For completeness, we recall the definition.
Definition 2.1 Let 
$\mathcal {M}_{0}(\mathbb {P}^r,d)$ be the category whose objects are diagrams
such that:
•
$S$ is a $k$-scheme;• the morphism
$\pi : C \to S$ is a projective flat family of curves isomorphic to $\mathbb {P}^1$;• the degree of
$f^*\mathcal {O}_{\mathbb {P}^r}(1)$ on the geometric fibers of $\pi : C \to S$ is $d$.
As a consequence of the third point, the restriction of 
$f$ on the geometric fibers of 
$\pi : C \to S$ is, in particular, not constant. Arrows are cartesian diagrams:
The category 
$\mathcal {M}_{0}(\mathbb {P}^r,d)$ is naturally a category fibered in groupoids over the category 
$(\text {Sch}/k)$ of 
$k$-schemes. It is a Deligne–Mumford stack; see, for example, [Reference Behrend and ManinBM96, Theorem 3.14]. As an example of a moduli point with non-trivial isotropy, let 
$f_d: \mathbb {P}^1 \to \mathbb {P}^1$ be defined as 
$f_d(x:y) = (x^d:y^d)$ and let 
$\iota _L:\mathbb {P}^1\to \mathbb {P}^r$ be the inclusion of 
$\mathbb {P}^1$ as a line in 
$\mathbb {P}^r$; then 
$(\mathbb {P}^1, \iota _L\circ f_d)\in \mathcal {M}_{0}(\mathbb {P}^r,d)$ has isotropy group 
$\mu _d$.
Observe that 
$\mathcal {M}_{0}(\mathbb {P}^r,d)$ has a structure of a global quotient by a linear algebraic group. Let 
$E$ be the standard representation of 
$\text { GL}_2$. We identify the projective line as
\[ \mathbb{P}^1 \cong \mathbb{P}(E). \]
Consider the vector space of homogeneous forms of degree 
$d$ over 
$\mathbb {P}^1$
\[ W_d:= H^0(\mathbb{P}^1,\mathcal{O}_{\mathbb{P}^1}(d)) = \text{Sym}^d(E^\vee), \]
where 
$E^\vee$ is the dual of the representation 
$E$.
The set of regular maps 
$\mathbb {P}^1 \to \mathbb {P}^r$ of degree 
$d$ is an open subset 
$U_{r,d}$ of 
$\mathbb {P} ( W_d^{\oplus r+1} )$. More precisely, a general element 
$f$ of 
$U_{r,d}$ can be written as
\[ f= \big[ f_1(x,y), \ldots, f_{r+1} (x,y) \big], \]
where:
• for all
$i=1, \ldots, r+1$, the polynomial in two variables $f_i(x,y)$ is homogeneous of degree $d$;• the map
$f$ is free of base points, in other words, the polynomials $f_i(x,y)$ have no common factors.
Call 
$\Delta _{r,d}$ the complement of 
$U_{r,d}$ in 
$\mathbb {P} ( W_d^{\oplus r+1} )$ and 
$\widehat {U}_{r,d}$ the affine cone over 
$U_{r,d}$, that is, the preimage of 
$U_{r,d}$ via the tautological map
\[ W_d^{\oplus r+1} \backslash 0 \to \mathbb{P} \big( W_d^{\oplus r+1} \big). \]
One has the following isomorphism of stacks (see [Reference Fulton and PandharipandeFP97, § 2] for a more general result):
\begin{equation} \mathcal{M}_{0}(\mathbb{P}^r, d) \cong \big[ U_{r,d} / \text{ PGL}_2 \big], \end{equation}
where the action of 
$\text { PGL}_2$ on 
$U_{r,d}$ is given by
\begin{equation} (A \cdot [f_1, f_2, \ldots, f_{r+1}])(x,y) = [f_1 (A^{-1}(x,y)), f_2(A^{-1}(x,y)), \ldots, f_{r+1}(A^{-1}(x,y))]. \end{equation}The use of the inverse matrix is necessary to have a well-defined left action.
Lemma 2.2 Let 
$H$ be a normal subgroup of a linear group 
$G$ and let 
$X$ be a quasi-projective scheme equipped with a 
$G$-action. Assume that 
$H$ acts freely on 
$X$ so that the quotient 
$X/H$ is a quasi-projective scheme as well. Then we have an isomorphism of quotient stacks:
\[ [ X / G ] \cong [ (X/H) / (G/H) ] \]
Proof. See, for example, [Reference HeinlothHei05, Example 3.3].
Remark 2.3 A consequence of Lemma 2.2 is the induced isomorphism of equivariant intersection rings:
\[ A^*_G(X) \cong A^*_{G/H}(X/H). \]
For a direct proof of this isomorphism see [Reference Molina Rojas and VistoliMRV06, Lemma 2.1].
From now on, assume the degree 
$d$ is odd.
Proposition 2.4 Let 
$d=2s+1$ be a positive odd integer. The stack 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$ is isomorphic to the quotient stack
\[ \mathcal{M}_{0}(\mathbb{P}^r, d) \cong \big[ \widehat{U}_{r,d} / \text{ GL}_2 \big], \]
where the action of 
$\text { GL}_2$ is
\[ A \cdot (f_0, f_1, \ldots, f_{r}) (x,y) = \det{A}^{s+1} (f_0 (A^{-1}(x,y)), f_1(A^{-1}(x,y)), \ldots, f_{r}(A^{-1}(x,y))). \]
Proof. Apply Lemma 2.2 with the substitutions
\[ X= \widehat{U}_{r,d}; \quad G=\text{ GL}_2; \quad H=\mathbb{G}_m. \]
Here 
$\mathbb {G}_m$ is normal in 
$\text { GL}_2$; one must describe the induced action of 
$\mathbb {G}_m$ on 
$\widehat {U}_{r,d} \subset W_d^{\oplus r+1}$.
Refer to the exact sequence of groups:
\[ 1 \to \mathbb{G}_m \xrightarrow{\varphi} \text{ GL}_2 \xrightarrow{\pi} \text{ PGL}_2 \to 1. \]
Let 
$\lambda \in \mathbb {G}_m$ and 
$\varphi (\lambda )= \big [ \begin {smallmatrix} \lambda & 0\\ 0 & \lambda \end {smallmatrix} \big ]=:A$, we have
\begin{align*} A \cdot (f_1, f_2, \ldots, f_{r+1}) (x,y) &= \det{A}^{s+1} (f_1 (A^{-1}(x,y)), f_2(A^{-1}(x,y)), \ldots, f_{r+1}(A^{-1}(x,y))) \\ & = \lambda^{2(s+1)} \frac{1}{\lambda^{d}}(f_1, f_2, \ldots, f_{r+1}) (x,y) = \lambda (f_1, f_2, \ldots, f_{r+1}) (x,y), \end{align*}
therefore 
$\widehat {U}_{r,d}/\mathbb {G}_m = U_{r,d}$. Note that the action of 
$\mathbb {G}_m$ is free on 
$\widehat {U}_{r,d}$. Lemma 2.2 implies
\[ \big[ \widehat{U}_{r,d} / \text{ GL}_2 \big] \cong \big[ U_{r,d} / \text{ PGL}_2 \big], \]
where the action of 
$\text { PGL}_2$ over 
$U_{r,d}$ is as in (4). We conclude thanks to isomorphism (3).
3. Generators and relations
By Proposition 2.4, we are reduced to computing the equivariant intersection ring 
$A^*_{\text { GL}_2}( \widehat {U}_{r,d} )$. First, we recall some facts about equivariant Chow rings we will use and set notation. Let 
$T$ denote the maximal torus for 
$\text { GL}_2$ represented by diagonal matrices and consider the induced morphism 
$Bi: BT \to B\text { GL}_2$. We denote by 
$E$ the standard representation of 
$\text { GL}_2$, which we think of as (the pull-back to the point via the quotient map 
$pt \to B\text { GL}_2$ of) a rank-two vector bundle over 
$B\text { GL}2$. As the Chern classes of 
$E$ are frequently used, we denote 
$c_i(E)$ simply by 
$c_i$. The pull-back 
$Bi^\ast (E^\vee )$ splits as the direct sum of two line bundles on 
$BT$: the characters 
$\lambda _1, \lambda _2$ are given by the two coordinate projections of 
$T$.
Denoting 
$A^{*}_T = A^{ *}_T(pt.)$, it is known (see, e.g., [Reference Hori, Katz, Klemm, Pandharipande, Thomas, Vafa, Vakil and ZaslowHKK+03, Chapter 4]) that 
$A^{*}_T=\mathbb {Z} [ l_1, l_2 ]$, with 
$l_i = c_1( \lambda _i)$. By a slight abuse of notation we also denote by 
$l_i$ the Chern roots of the vector bundle 
$E^\vee$, because we have
\begin{align*} Bi^\ast c_1&=-(l_1+l_2),\\ Bi^\ast c_2 &= l_1 l_2. \end{align*}
The Weyl group 
$S_2$ acts on 
$A^*_T$ by permuting the classes 
$l_i$ and 
$A^*_{\text { GL}_2}=( A^*_T )^{S_2}$ (see [Reference Edidin and GrahamEG98a, Proposition 6]).
Consider the following commutative 
$\text { GL}_2$-equivariant diagram
where the horizontal arrows are the natural open inclusions and the vertical arrows are the natural quotient maps by the action of 
$\mathbb {G}_m$. The vertical maps may be interpreted as principal 
$\mathbb {G}_m$-bundles associated to the 
$\text { GL}_2$-equivariant line bundle 
$\mathcal {D}^{\otimes s+1} \otimes \mathcal {O}(-1)$, where 
$\mathcal {O}(-1)$ is the tautological bundle over 
$\mathbb {P} ( W_d^{\oplus r+1} )$ and 
$\mathcal {D}$ is the one-dimensional representation of 
$\text { GL}_2$ associated to the determinant 
$\bigwedge ^2 E$. The first Chern class of 
$\mathcal {D}$ is 
$c_1(\mathcal {D})=c_1$, therefore we have
\[ c_1 \big( \mathcal{D}^{\otimes s+1} \otimes \mathcal{O}(-1) \big)=(s+1)c_1 - H, \]
where 
$H$ is the canonical equivariant lift of the hyperplane class of 
$\mathbb {P} ( W_d^{\oplus r+1} )$. By arguing as in Lemma 3.2 of [Reference Edidin and FulghesuEF09], the pull-back morphism
\[ \pi^*: A^*_{\text{ GL}_2} \big( U_{r,d} \big) \to A^*_{\text{ GL}_2} \big( \widehat{U}_{r,d} \big) \]
is surjective and its kernel is generated by 
$H-(s+1)c_1$. We may therefore determine 
$A^*_{\text { GL}_2} ( \widehat {U}_{r,d} )$ from a presentation of the ring 
$A^*_{\text { GL}_2} ( U_{r,d})$ by applying the substitution 
$H=(s+1)c_1$.
In order to compute 
$A^*_{\text { GL}_2} ( U_{r,d} )$, we consider the following exact sequence of 
$A^*_{\text { GL}_2}$-modules:
\[ A^*_{\text{ GL}_2}\big( \Delta_{r,d} \big) \xrightarrow{i_*} A^*_{\text{ GL}_2}\big( \mathbb{P} \big( W_d^{\oplus r+1} \big) \big) \xrightarrow{j^*} A^*_{\text{ GL}_2}\big( U_{r,d} \big) \to 0. \]
Using standard techniques as in [Reference Fulghesu and VistoliFV18, § 3.2], we have the following isomorphism:
\begin{equation} A^*_{\text{ GL}_2}\big( \mathbb{P} \big( W_d^{\oplus r+1} \big) \big) \cong \frac{\mathbb{Z}[c_1,c_2,H]}{(P_{r,d}(H))}, \end{equation}where
\begin{equation} P_{r,d}(H)= \prod_{k=0}^d (H+(d-k)l_1 + kl_2)^{r+1}. \end{equation}In conclusion, we have
\begin{equation} A^* \big( \mathcal{M}_{0}(\mathbb{P}^r, d) \big) \cong \frac{A^*_{\text{ GL}_2}\big( \mathbb{P} \big( W_d^{\oplus r+1} \big) \big)}{(\text{Im}(i_*), H-(s+1)c_1)} \cong \frac{\mathbb{Z}[c_1,c_2,H]}{(\text{Im}(i_*), H-(s+1)c_1,P_{r,d}((s+1)c_1))}, \end{equation}
where 
$\text {Im}(i_*)$ is the image of the push-forward 
$i_*$. The goal is now to compute generators for the ideal 
$\text {Im}(i_*)$.
Let 
$X$ be a 
$G$-scheme and 
$\Delta \xrightarrow {i} X$ an equivariant closed embedding. A consolidated method to determine the image of the group homomorphism
\[ A_G^*(\Delta) \xrightarrow{i_*} A_G^*(X), \]
is to use a so-called equivariant envelope of 
$\Delta$. Recall that an envelope 
$\widetilde {\Delta } \xrightarrow {\widetilde {\pi }} \Delta$, see [Reference FultonFul98, Definition 18.3], is a proper map such that for every subvariety 
$V$ of 
$\Delta$, there is a subvariety 
$\widetilde {V}$ of 
$\widetilde {\Delta }$ such that the morphism 
$\widetilde {\pi }$ maps 
$\widetilde {V}$ birationally onto 
$V$. In the category of 
$G$-schemes, 
$\widetilde {\pi }$ is called an equivariant envelope, see [Reference Edidin and GrahamEG98a, § 2.6], if 
$\widetilde {\pi }$ is 
$G$-equivariant and if one can choose 
$\widetilde {V}$ to be 
$G$-invariant whenever 
$V$ is 
$G$-invariant. An equivariant envelope 
$\widetilde {\Delta } \xrightarrow {\widetilde {\pi }} \Delta$ for a closed subscheme 
$\Delta \xrightarrow {i} X$ is especially helpful when one can explicitly describe the Chow group of 
$\widetilde {\Delta }$ and the image of the group homomorphism
\[ A_G^*(\widetilde{\Delta}) \xrightarrow{(i \circ \widetilde{\pi})_*} A_G^*(X). \]
As the group homomorphism 
$\widetilde {\pi }_\ast$ is surjective (see [Reference Edidin and GrahamEG98a, Lemma 3] and [Reference FultonFul98, Lemma 18.3(6)]), one has the following result.
Theorem 3.1 Let 
$X$ be a 
$G$-scheme and 
$\Delta \xrightarrow {i} X$ an equivariant closed embedding. If 
$\widetilde {\Delta } \xrightarrow {\widetilde {\pi }} \Delta$ is an equivariant envelope of 
$\Delta$, then
\[ (i \circ \widetilde{\pi})_* \big( A_{G}^* ( \widetilde{\Delta}) \big) = { i_* }\big( A_{G}^* \big( \Delta \big) \big). \]
Returning to the computation, we construct an equivariant envelope for the locus of degenerate maps 
$\Delta _{r,d}$.
Definition 3.2 For every 
$i=1, \ldots, d$, denote by 
$Z_i$ the subspace of 
$\mathbb {P} ( W_d^{\oplus r+1} )$ representing 
$(r+1)$-tuples of polynomials with a common factor of degree 
$i$, but not 
$i+1$:
\begin{equation} Z_i = \{(f_1, \ldots, f_{r+1}) | \deg(\gcd(f_1, \ldots, f_{r+1}) = i \}. \end{equation} The family 
$\{ Z_i\}_{i=1, \ldots, d}$ is an equivariant stratification of 
$\Delta _{r,d}$, in the sense of [Reference Di Lorenzo, Fulghesu and VistoliDLFV21, Definition 1.2].
Define
\begin{equation} \widetilde{Z}_i := \mathbb{P}(W_i) \times \mathbb{P} \big( W_{d-i}^{\oplus r + 1} \big) \end{equation}and the morphisms
\begin{equation}
\begin{aligned} \pi_i:
\widetilde{Z}_i & \to \mathbb{P} \big( W_d^{\oplus r+1}
\big) \\ ([c(x,y)],[g_1(x,y), g_2(x,y), \ldots,
g_{r+1}(x,y)]) & \mapsto [c(x,y) \cdot g_1(x,y), c(x,y) \\ &\quad\ \ \cdot g_2(x,y), \ldots, c(x,y)\cdot g_{r+1}(x,y)].
\end{aligned} \end{equation}
Proposition 3.3 We use the notation 
$\widetilde {Z} := \bigsqcup _{i=1, \ldots, d} \widetilde {Z}_i$ and 
$\pi := \sqcup \pi _i$. Denoting by 
$\widetilde \pi$ the restriction of 
$\pi$ onto its image 
$\Delta _{r,d}$, we have that
\[ \widetilde\pi: \widetilde{Z}\to \Delta_{r,d} \]
is an equivariant envelope on 
$\Delta _{r,d}$.
Proof. This proposition may be proved following the argument in [Reference VistoliVis98, Lemma 3.2]. Observe that each 
$\widetilde {Z}_i$ maps to the closure 
$\overline {Z}_i$ of a stratum of 
$\Delta _{r,d}$. The morphism 
$\widetilde {\pi }$ is proper and 
$\text { GL}_2$-equivariant. The morphisms from the components 
$\widetilde {Z}_i \to \overline {Z}_i$ are birational and isomorphisms over 
$\overline {Z}_i\smallsetminus \overline {Z}_{i+1}$. Given 
$V$ an irreducible 
$\text { GL}_2$-invariant subvariety of 
$\overline {Z}_i$ not contained in 
$\overline {Z}_{i+1}$, one may take the preimage of 
$V \smallsetminus \overline {Z}_{i+1}$ in 
$\widetilde {Z}_i$ and close it to obtain 
$\widetilde {V}$. Then the map 
$\widetilde {V}\to V$ is birational and 
$\text { GL}_2$-equivariant, and thus 
$[\widetilde {V}]$ pushes forward to 
$[V]$, which completes the proof.
Corollary 3.4 We have the identity
\[ \pi_* \big( A_{\text{ GL}_2}^* ( \widetilde{Z}) \big) = { i_* }\big( A_{\text{ GL}_2}^* \big( \Delta_{r,d} \big) \big). \]
For the next definition, we adopt the notation in the following diagram.
Definition 3.5 For all 
$i=1, \ldots, d$, denote by 
$h_{i} = p_1^\ast c_1^{eq} (\mathcal {O}_{\mathbb {P}(W_i) }(1))$ the (pull-back via the first projection of the) canonical equivariant lift of the hyperplane class on the first component of 
$\widetilde {Z}_i = \mathbb {P}(W_i) \times \mathbb {P} ( W_{d-i}^{\oplus r + 1} )$. In addition, denote by 
$H = c_1^{eq} (\mathcal {O}_{ \mathbb {P}(W_d^{\oplus r+1} ) }(1))$ and by 
$\eta _i = p_2^\ast c_1^{eq} (\mathcal {O}_{ \mathbb {P} ( W_{d-i}^{\oplus r + 1})}(1))$. Define the classes
\[ \alpha_{i,k}(H):= \pi_{i_*} \big( h_i^k\big) \in A_{\text{ GL}_2}^* \big( \mathbb{P}(W_d^{\oplus r+1} ) \big). \]
Proposition 3.6 We have the ideal identity
\[ i_* \big( A_{\text{ GL}_2}^* \big( \Delta_{r,d} \big) \big) = \big( \alpha_{i,k}(H)\big)_{i=1, \ldots, d; \; k=0, \ldots, i}. \]
Proof. Using Corollary 3.4, it suffices to show that 
$\pi _* ( A_{\text { GL}_2}^* ( \widetilde {Z}) )$ is contained in the ideal 
$I$ generated by the classes 
$\alpha _{i,k}(H)$. From (10),
\begin{equation} \pi_i^\ast(H) = h_i+\eta_i. \end{equation} We prove that any class of the form 
$\pi _{i_\ast } (h_i^{k} \eta _i^{m})$ is in 
$I$ by induction on 
$m$. As the classes 
$h_i^k \eta _i^m$ generate 
$A_{\text { GL}_2}^*(\widetilde {Z}_i)$ over 
$A_{\text { GL}_2}^*$, this will prove the proposition. For 
$m=0$, 
$k>i$, note that the class 
$\pi _{i_\ast }(h_i^k)$ is a linear combination of the classes 
$\alpha _{i,k}(H)$, 
$k\leq i$, with coefficients in 
$\mathbb {Z}[l_1, l_2]$ (this can be seen by using the relation in the equivariant Chow ring of the left factor to express 
$h_i^k$ as a polynomial of degree at most 
$i$ in 
$h_i$, and then pushing forward); hence, the base case 
$m = 0$ is established.
Using projection formula and (12) one obtains the following equalities:
\[ H \pi_{i_\ast}(h_i^k \eta_i^{m-1}) = \pi_{i_\ast}(h_i^k \eta_i^{m-1} \pi_i^\ast H) = \pi_{i_\ast}(h_i^k \eta_i^{m-1} (h_i+\eta_i)) = \pi_{i_\ast}(h_i^{k+1} \eta_i^{m-1} ) + \pi_{i_\ast}(h_i^{k} \eta_i^{m} ). \]
Solving
\[ \pi_{i_\ast}(h_i^{k} \eta_i^{m}) = H \pi_{i_\ast}(h_i^k \eta_i^{m-1}) - \pi_{i_\ast}(h_i^{k+1} \eta_i^{m-1} ) \]
completes the inductive step.
Lemma 3.7 For every value of 
$r,d$, we have 
$P_{r,d}(H) \in Im(i_\ast )$.
Proof. The case 
$d=1$ is treated by direct inspection: it is known that 
$\alpha _{1,0}, \alpha _{1,1}$ generate the ideal of relations for the integral Chow ring of Grassmannians ([Reference Eisenbud and HarrisEH16, Theorem 5.26]).
For 
$d\geq 2$, we consider the component 
$\widetilde {Z}_2$ of the equivariant envelope and the point 
$P = (0:1:0) = [xy]\in \mathbb {P}(W_2).$ The point 
$P$ is invariant with respect to the action of the maximal torus of 
$\text { GL}_2$, and its class is symmetric in the two torus weights. It follows that 
$P$ defines a class in 
$A^\ast _{\text { GL}_2}(\mathbb {P}(W_2))$ (see the discussion at the beginning of § 3). The class 
$\pi _{2_\ast }(p_1^\ast ([P]))$ is contained in the ideal of relations. The lemma is proved by showing that such class divides 
$P_{r,d}(H)$.
The map 
${\pi _2}_{|p_1^{-1}([P])}$ has degree one onto the coordinate linear subspace of 
$\mathbb {P}(W_d^{\oplus r+1})$ obtained by setting to zero all homogeneous coordinates corresponding to monomials of the form 
$x^d$ or 
$y^d$. It follows that
\begin{equation} \pi_{2_\ast}(p_1^\ast([P])) = \big((H+dl_1)(H+dl_2)\big)^{r+1}, \end{equation}
which indeed is a factor of 
$P_{r,d}(H)$.
Using Proposition 3.6, Lemma 3.7 and recalling the notational convention 1.2, we have obtained from (7) the following presentation for the Chow ring of 
$\mathcal {M}_{0}(\mathbb {P}^r, d)$.
Theorem 3.8 For any odd positive integer 
$d$ and any integer 
$r\geq 0$ we have
\begin{equation} A^* \big( \mathcal{M}_{0}(\mathbb{P}^r, d) \big) \cong \frac{\mathbb{Z}[c_1,c_2]}{(\alpha_{i,k})_{i=1, \ldots, d, k=0, \ldots, i}}. \end{equation}Remark 3.9 Although for 
$r=0$ the constructions in this section do not yield a space of stable maps (but rather a space of quasi-maps as in [Reference Ciocan-Fontanine, Kim and MaulikCFKM14]), we find convenient to include this case in our study because we compute some of the generating relations inductively on 
$r$, with 
$r=0$ being the base case.
4. Eliminating redundant relations
In this section we reduce the number of generators of the ideal of relations in the quotient ring (14). More precisely, we prove that the ideal
\[ \big(\pi_* \big( A_{\text{ GL}_2}^* ( \widetilde{Z}) \big)\big)=(\alpha_{i,k})_{i=1, \ldots, d, k=0, \ldots, i} \]
is generated by 
$\alpha _{1,0}, \alpha _{1,1},$ and 
$\alpha _{i,0}$ for all positive integers 
$i$ that are powers of a prime number.
The goal is to prove that the image of the push-forward map
\[ \pi_{i*}: A_{\text{ GL}_2}^* \big(
\mathbb{P}(W_i) \times \mathbb{P} \big( W_{d-i}^{\oplus r +
1}\big)\big) \to A_{\text{ GL}_2}^*
\big( \mathbb{P} \big( W_{d}^{\oplus r + 1}
\big)\big) \]
is contained in the image of the push-forward maps 
$\pi _{a*}$ with 
$a$ less than 
$i$, whenever 
$i$ is not the power of a prime number. Consider the commutative diagram
in which the only morphism that has not been already defined is 
$\psi _i:=\bigsqcup \pi _a \times \text {id}$. In this context, the morphism 
$\pi _a: \mathbb {P}(W_{a}) \times \mathbb {P}(W_{i-a}) \to \mathbb {P}(W_i)$ is defined as
\[ \pi_{a} ([c(x,y)],[g(x,y)]) = [c(x,y) \cdot g(x,y)]. \]
In other words, on the left-hand side of diagram (
15), the morphisms 
$\pi _a$ are considered in the case 
$r=0$, whereas in the rest of the diagram, the morphisms 
$\pi _{k}$ are considered for a fixed value of 
$r$.
As the diagram is commutative, in order to show that the image of the push-forward map 
$\pi _{i*}$ is contained in the image of the push-forward maps 
$\pi _{a*}$ with 
$a$ less than 
$i$, it is enough to show that the push-forward 
$\psi _{i*}$ is surjective. Moreover, it suffices to verify that 
$\psi _{i*}$ is surjective when considering the torus-equivariant intersection groups. Therefore, we focus on the push-forward map:
\[ \pi_{a*}: A^{*}_{T} \big( \mathbb{P}(W_{a}) \times \mathbb{P}(W_{i-a}) \big) \to A^{*}_{T} \big( \mathbb{P}(W_i) \big). \]
Remark 4.1 Arguing as in Proposition 3.6, the image of 
$\pi _{a*}$ is generated by the classes 
$\alpha _{a,k}(h_i):=\pi _{a*}(h_a^k)$ for 
$k=0, \ldots, a$. As 
$\pi _{a*}$ is a homomorphism of 
$A^*_{T}$-modules, one can also view the image of 
$\pi _{a*}$ as generated by the classes
\begin{equation} \widetilde{\alpha}_{a,k}:= \pi_{a*}(P_{a,k}(h_a)), \end{equation}
where 
$\{ P_{a,k}(h_a) \}_{k=0, \ldots, a}$ is a suitable family of monic polynomials of degree 
$k$ that we define as
\[ P_{a,k}(h_a):=\prod_{s=0}^{k-1}(h_a + (a-s)l_1 + s l_2). \]
In other words, 
$P_{a,k}(h_a)$ is the equivariant Chow class of the locus of polynomials in 
$W_a$ that are divisible by 
$y^k$. Note that 
$P_{a,0}(h_a)=1$. In the following lemma we determine the classes 
$\widetilde {\alpha }_{a,k}$.
Lemma 4.2 Let 
$\widetilde {\alpha }_{a,k}$ be the class in 
$A_T^{*}(\mathbb {P}(W_i))$ defined in (16). Then we have the following identity:
\[ \widetilde{\alpha}_{a,k}=\binom{i-k}{a-k} P_{i,k}(h_i). \]
Proof. Let 
$L_{a,k} \subset \mathbb {P}(W_a) \times \mathbb {P}(W_{i-a})$ be the locus of pairs of polynomials where the first is a multiple of 
$y^k$. The locus 
$L_{a,k}$ is invariant for the action of the torus 
$T$ and its equivariant class is 
$P_{a,k}(h_a)$. The restriction of the map
\[ \pi_a: \mathbb{P}(W_a) \times \mathbb{P}(W_{i-a}) {\to \mathbb{P}(W_i)} \]
to 
$L_{a,k}$ is finite of generic degree 
$\binom {i-k}{a-k}$ onto its image. This is due to the following facts:
• the image of
$L_{a,k}$ is the locus of polynomials of degree $i$ which are divisible by $y^{k}$;• let
$R(x,y)=y^k S(x,y)$ be a generic homogeneous polynomial of degree $i$ which is divisible by $y^k$; because we are in an algebraically closed field and assuming by generality that $S(x,y)$ has $i-k$ distinct roots, there are exactly $\binom {i-k}{a-k}$ ways to choose a factor $F(x,y)$ of $S(x,y)$ of degree $a-k$ so that $[y^kF(x,y), S(x,y)/F(x,y)]$ in $\mathbb {P}(W_a) \times \mathbb {P}(W_{i-a})$ maps to $R(x,y)$.
To conclude the proof, we note that 
$[L_{a,k} ]=P_{a,k}(h_a)$ and 
$[\pi _{a}(L_{a,k}) ]=P_{i,k}(h_i)$, therefore we have
\[ \widetilde{\alpha}_{a,k}=\binom{i-k}{a-k} P_{i,k}(h_i).\quad \]
Theorem 4.3 The ideal of relations 
$(\alpha _{i,k})_{i=1, \ldots, d, k=0, \ldots, i}$ is generated by the classes 
$\alpha _{1,0}$, 
$\alpha _{1,1}$ from 
$\widetilde {Z}_1$ and the push-forwards 
$\alpha _{i,0}$ of the fundamental classes of 
$\widetilde {Z}_i$ where 
$i$ is the power of a prime number.
Proof. Assume that 
$i>1$ and fix a positive integer 
$1\leq k\leq i$. We want to show that there exists a monic polynomial in 
$h_i$ of degree 
$k$ that is in the image of 
$\psi _*$. For every integer 
$a< i$ and integer 
$j \leq \min (a,k)$, we have that 
$h_i^{k-j}\widetilde {\alpha }_{a,j}$ is a polynomial in 
$h_j$ with leading coefficient equal to 
$\binom {i-j}{a-j}$. If 
$k\geq 2$ we can choose 
$a=j=k-1$, so that the polynomial 
$\widetilde {\alpha }_{k-1,k-1}$ is monic in 
$h_j$. If 
$k=1$, then 
$k< i$ and 
$\widetilde {\alpha }_{1,1}$ is monic.
For the case 
$k=0$, the only homogeneous monic polynomial in 
$h_i$ of degree zero is the fundamental class 1. We know that the greatest common divisor of the binomials 
$\binom {i}{a}$ for 
$a$ going from 
$1$ to 
$i-1$ is in the image of 
$\psi _*$. It is a consequence of Lucas's theorem [Reference LucasLuc78] that such the greatest common denominator (GCD) is 1 when 
$i$ is not the power of a prime number (and the prime number otherwise) and this concludes the proof.
5. Relations from $Z_1$
In this section we compute the relations coming from the first envelope 
$Z_1$. We exhibit generating functions, whose coefficients are functions of the degree 
$d$, encoding the classes 
$\alpha _{1,i}^r$ for all values of 
$r$.
Theorem 5.1 For 
$k= 0,1$, consider the 
$A^* ( \mathcal {M}_{0}(\mathbb {P}^r, d))$ valued generating functions:
\[ \mathcal{A}_{1,k}(c_1, c_2, d) = \sum_{r=0}^{\infty} \pi_{1, \ast} [h_1^k] = \sum_{r=0}^{\infty} \alpha^{r}_{1,k}, \]
encoding the push-forwards of the fundamental class and equivariant hyperplane class from the first component 
$Z_1$ of the envelope. We have
\begin{gather} \mathcal{A}_{1,0}(c_1, c_2, d) = \frac{d}{\bigl(1+(({d-1})/{2})c_1\bigr)\bigl(1-(({d+1})/{2})c_1\bigr)+d^2c_2}, \end{gather}
\begin{gather} \mathcal{A}_{1,1}(c_1, c_2, d) = \frac{1+(({d-1})/{2})c_1}{\bigl(1+(({d-1})/{2})c_1\bigr)\bigl(1-(({d+1})/{2})c_1\bigr)+d^2c_2}-1. \end{gather} We begin by describing the strategy of proof of Theorem 5.1. The starting point is the following commutative diagram, comparing the maps 
$\pi _1$ from (11) for target dimensions 
$r$ and 
$r+1$:
where the maps denoted 
$i_r$ are the linear inclusions into the subspace where the homogeneous coordinates corresponding to the 
$(r+2)$th direct summand are equal to zero. The equality of the push-forwards along the two different compositions in (
) gives rise to recursive relations that determine the classes 
$\alpha _{1,k}^{r+1}$ from the classes 
$\alpha _{1,k}^{r}$. Appropriately organizing the recursive relations gives rise to a system of functional equations. The generating functions 
$\mathcal {A}_{1,k}$ from (17) and (18) are then shown to satisfy the system of functional equations and to have the correct initial conditions, corresponding to the case 
$r=0$ (the target is a point).
Proof. We first establish some conventions meant to simplify notation: the two horizontal arrows of diagram (19) are both denoted by 
$\pi _1$ and we let the context determine which map any given equation is referring to. Similarly, the equivariant hyperplane classes for the three projective spaces in both rows of (19) are denoted 
$h_1,\eta _1$ and 
$H$ (as in § 3); each class in the top row is the pull-back of the corresponding class in the bottom row. Thus, for instance, any polynomial in 
$H, c_1, c_2$ denotes both a class for 
$\mathbb {P}(W_{d}^{\oplus r+2})$ and one for 
$\mathbb {P}(W_{d}^{\oplus r+1})$, with the latter being the pull-back via 
$i_r$ of the former.
The commutativity of the diagram (19) implies that for 
$k=0,1$,
\begin{equation} i_{r\ast}(\pi_{1_{\ast}}(h_1^k)) =\pi_{1_{\ast}}((\text{id}\times i_r)_\ast(h_1^k)). \end{equation} Starting with the left-hand side of (20), 
$\pi _{1_{\ast }}(h_1^k) = \alpha ^{r}_{1,k}(H)$ by definition, and by the projection formula one has
\begin{equation} i_{r_{\ast}}(\alpha^{r}_{1,k}(H)) =\alpha^{r}_{1,k}(H) P_d(H), \end{equation}
where 
$P_d(H) := P_{0,d}(H)$ from (6).
For the right-hand side of (20), we apply the projection formula to obtain
\begin{equation} (\text{id}\times i_r)_\ast(h_1^k) = h_1^k P_{d-1}(\eta_1). \end{equation}
Using that 
$H = h_1+\eta _1$ (where we omit 
$\pi _1^\ast$ from the notation for the pull-back of the class 
$H$), and the presentation of the equivariant Chow ring of 
$\mathbb {P}(W_1)$, we may write
\begin{equation} h_1^k P_{d-1}(\eta_1) = R_{1,k,0}^{r,d}(H,c_1, c_2)+ R_{1,k,1}^{r,d}(H,c_1,c_2)h_1, \end{equation}
where the right-hand side of (23) is the remainder of the division of 
$P_{d-1}(H-h_1)$ by the polynomial 
$P_{1}(h_1)=(h_1^2- c_1h_1 +c_2)$.
Pushing forward and using the projection formula, we then obtain
\begin{equation} \pi_{1_{\ast}}((\text{id}\times i_r)_\ast(h_1^k)) = R_{1,k,0}^{r,d}(H,c_1, c_2)\alpha^{r+1}_{1,0}(H)+ R_{1,k,1}^{r,d}(H,c_1,c_2)\alpha^{r+1}_{1,1}(H). \end{equation} From (20), (21) and (23), by substituting 
$H= (({d+1})/{2}) c_1$ one obtains the square size 
$2$ linear system
\begin{equation} P_d \alpha_{1,k}^{r} = R_{1,k,0}^{r,d}\alpha^{r+1}_{1,0}+ R_{1,k,1}^{r,d}\alpha^{r+1}_{1,1}, \end{equation}
where 
$k = 0,1$.
The following claim shows that all coefficients in (25) are divisible by
\[
P_{d-2}:=P_{d-2}\biggl(\frac{d-1}{2}c_1\biggr).
\]
Claim 5.2 We have the following identities:
\begin{align} P_d &= \biggl( d^2 c_2-\frac{d^2 -1}{4} c_1^2\biggr)P_{d-2}, \end{align}
\begin{align} R_{1,0,0}^{r,d} &= \biggl( \frac{d+1}{2} c_1 \biggr) P_{d-2}, \end{align}
\begin{align} R_{1,0,1}^{r,d} &= -d P_{d-2}, \end{align}
\begin{align} R_{1,1,0}^{r,d} &= dc_2P_{d-2}, \end{align}
\begin{align} R_{1,1,1}^{r,d} &= \biggl(\frac{1-d}{2}c_1\biggr)P_{d-2}. \end{align}Using the results from Claim 5.2, proved at the end of the section, the linear system (25) simplifies to
\begin{equation} \biggl( d^2 c_2-\frac{d^2 -1}{4} c_1^2 \biggr)\biggl[ \begin{array}{c} \alpha^{r}_{1,0}\\ \alpha^{r}_{1,1} \end{array} \biggr] = \left[ \begin{array}{cc} \dfrac{d+1}{2} c_1 & -d\\ d c_2 & \dfrac{1-d}{2}c_1 \end{array} \right] \biggl[ \begin{array}{c} \alpha^{r+1}_{1,0}\\ \alpha^{r+1}_{1,1} \end{array} \biggr]. \end{equation}
The linear system (31) may be solved for the 
$\alpha _{1,k}^{r+1}$ to obtain
\begin{equation} \begin{aligned} \alpha^{r+1}_{1,0} & = \frac{1-d}{2}c_1\alpha^{r}_{1,0}+ d \alpha^{r}_{1,1}, \\ \alpha^{r+1}_{1,1} & = -d c_2\alpha^{r}_{1,0}+ \frac{d+1}{2}c_1\alpha^{r}_{1,1}. \end{aligned} \end{equation}Together with the initial conditions
\begin{equation} \alpha_{1,0}^{0} = d, \quad \alpha_{1,1}^{0} = \frac{d+1}{2}c_1, \end{equation}
the equations in (32) for all 
$r\geq 0$ determine recursively all values of 
$\alpha _{1,k}^{r}$. To conclude the proof, it suffices to observe that (32) and (33) give rise to the system of functional equations
\begin{equation} \left\{
\begin{array}{@{}l} \mathcal{A}_{1,0}-d =
\dfrac{1-d}{2}c_1\mathcal{A}_{1,0}+ d \mathcal{A}_{1,1},\\
\mathcal{A}_{1,1} - \dfrac{d+1}{2}c_1 = -d
c_2\mathcal{A}_{1,0}+ \dfrac{d+1}{2}c_1\mathcal{A}_{1,1},
\end{array} \right. \end{equation}
together with the boundary conditions
\begin{equation} \mathcal{A}_{1,0}(0,0,d) = d, \quad \mathcal{A}_{1,1}(0,0,d) = 0. \end{equation}It is then immediate to verify that (34) and (35) are satisfied by the generating functions (17) and (18). Thus, Theorem 5.1 is proved (as soon as the identities from Claim 5.2 are established).
Proof of Claim 5.2 Equation (26) follows from the definition of the polynomial 
$P_d$ in terms of the weights 
$l_1$ and 
$l_2$, as defined in (6); substituting 
$H = (({d+1})/{2})c_1$ in the polynomial 
$P_{0,d}(H)$ and 
$H = (({d-1})/{2})c_1$ in the polynomial 
$P_{0,d-2}(H)$, it is immediate to see that the factors of 
$P_{d-2}$ are equal to the internal factors of 
$P_d$. It follows that the quotient 
$P_d/P_{d-2}$ consists of the product of the first and last terms of 
$P_d$:
\begin{equation} \frac{P_d}{P_{d-2}} = \biggl(\frac{d+1}{2}c_1+dl_1\biggr)\biggl(\frac{d+1}{2}c_1+dl_2\biggr). \end{equation}
Equation (26) follows from (36) by expanding and substituting 
$-l_1-l_2 = c_1, l_1l_2 = c_2$.
Equations (27), (28), (29) and (30) are proved by induction on odd values of 
$d$, with the base case 
$d=1$ easily established after noting 
$P_{-1}=1$.
We work in the quotient ring 
$\mathbb {Z}[h_1, c_1,c_2]/ (h_1^2-c_1h+c_2)$, adopting the convention that for any polynomial 
$q$, its image 
$[q]$ in the quotient ring is identified with the remainder of division by 
$h_1^2-c_1h+c_2$. From the definitions for the 
$(d+2)$-th case one may observe that
\begin{align} & P_{d+1}\biggl(\frac{d+3}{2}-h_1\biggr)\nonumber\\ &\quad =
\biggl(\frac{d+3}{2}c_1+(d+1)l_1-h_1\biggr)\biggl(\frac{d+3}{2}c_1+(d+1)l_2-
h_1\biggr) P_{d-1}\biggl(\frac{d+1}{2}-h_1\biggr).
\end{align}
By (23)
\begin{equation} \biggl[P_{d+1}\left(\frac{d+3}{2}-h_1\right) \biggr] = \big[ R^{r,d+2}_{1,0,0}+ R^{r,d+2}_{1,0,1}h_1 \big], \end{equation}so after symmetrizing the quadratic factor in (37) and replacing the last factor using the inductive hypothesis, one has
\begin{align} &\big[
R^{r,d+2}_{1,0,0}+ R^{r,d+2}_{1,0,1}h_1 \big]\nonumber\\ &\quad =
\biggl[\left(h_1^2 - 2c_1h_1 - \frac{(d+1)(d-3)}{4}c_1^2 +
(d+1)^2c_2 \right) \left( -dh_1+\frac{d+1}{2}c_1\right)
P_{d-2} \biggr].
\end{align}
In order to obtain (27) and (28) one must check that
\begin{align} \big[ R^{r,d+2}_{1,0,0}+ R^{r,d+2}_{1,0,1}h_1 \big] &= \biggl[ \biggl( -(d+2)h_1+\frac{d+3}{2}c_1\biggr) P_{d} \biggr] \nonumber\\ &= \biggl[ \biggl( -(d+2)h_1+\frac{d+3}{2}c_1\biggr)\biggl( d^2 c_2-\frac{d^2 -1}{4} c_1^2 \biggr) P_{d-2} \biggr] , \end{align}where the last equality is obtained by applying (26). It is then sufficient to verify
\begin{align} &\biggl[\biggl(h_1^2 - 2c_1h_1 - \frac{(d+1)(d-3)}{4}c_1^2 + (d+1)^2c_2 \biggr) \biggl( -dh_1+\frac{d+1}{2}c_1\biggr) \biggr] \nonumber\\ &\qquad = \biggl[ \biggl( -(d+2)h_1+\frac{d+3}{2}c_1\biggr)\biggl( d^2 c_2-\frac{d^2 -1}{4} c_1^2 \biggr) \biggr], \end{align}which is easily done.
In order to prove (29), (30), one has
\begin{align} \big[ R^{r,d}_{1,1,0}+ R^{r,d}_{1,1,1}h_1 \big] &= \biggl[h_1 P_{d-1}\biggl(\frac{d+1}{2}c_1-h_1\biggr) \biggr] = \big[ R^{r,d}_{1,0,0}h_1+ R^{r,d}_{1,0,1}h_1^2 \big]\nonumber\\ &= \big[- R^{r,d}_{1,0,1}c_2+ \big(R^{r,d}_{1,0,0}+c_1 R^{r,d}_{1,0,1}\big)h_1 \big], \end{align}from which the result follows by direct substitution.
6. Relations of type $\alpha _{i,0}$
In this section we exhibit formulas for the relations obtained by pushing forward the fundamental classes of the various components 
$Z_i$ of the envelope. These classes exhibit the following interesting structure: for any fixed values of 
$d,r$, the relations 
$\alpha _{i,0}$ are obtained for all 
$i$ via the action of a differential operator on a single monomial function.
Theorem 6.1 For any 
$d>0$, 
$r\geq 0$, 
$0\leq i \leq d$, the relations 
$\alpha _{i,0}\in A^\ast (\mathcal {M}_{0}(\mathbb {P}^r, d))$ are given by the formula
\begin{equation}
\alpha_{i,0}= \displaystyle \sum_{j=0}^{i} \frac{(-1)^{j}}{i!
(l_2-l_1)^i}\binom{i}{j}\biggl(\frac{P_{d}}
{\prod_{k = j}^{d-i+j}({c_1}/{2}+(k-{d}/{2})(l_2-l_1)
\bigr)}\biggr)^{r+1}. \end{equation}
Remark 6.2 We observe that in order to get from formula (43) to the generating function 
$\mathcal {A}_{i,0}(d)$ from the main theorem, it is just a matter of noticing the geometric series arising when adding (43) for all values of 
$r$.
We obtain formula (43) through an application of Atyiah–Bott localization, which we now recall.
Theorem 6.3 [Reference Edidin and GrahamEG98b, Theorem 2]
Define the 
$A^*_T$-module 
$\mathcal {Q}:= ((A^*_T)^+)^{-1}A^*_T$, where 
$(A^*_T)^+$ is the multiplicative system of homogeneous elements of 
$A^*_T$ of positive degree.
Let 
$X$ be a smooth 
$T$-variety and consider the locus 
$F$ of fixed points for the action of 
$T$. Let 
$F=\cup F_j$ be the decomposition of 
$F$ into irreducible components. For every 
$\gamma$ in 
$A^*_T(X)\otimes \mathcal {Q}$, we have the identity
\[ \gamma = \sum_{j} \frac{i_{F_j}^*(\gamma)}{c_{\rm top}^T(N_{F_{j}/X})}, \]
where 
$i_{F_j}$ is the inclusion of 
$F_j$ in 
$X$ and 
$N_{F_j/X}$ is the normal bundle of 
$F_j$ in 
$X$.
Proof of Theorem 6.1 In order to apply Theorem 6.3, we work with rational coefficients. Referring to diagram (11) for notation, we compute
\begin{equation} \alpha_{i,0} = \pi_{1_{\ast}}([\widetilde{Z}_i]) = \pi_{1_{\ast}}(p_1^\ast([\mathbb{P}(W_i)])) \end{equation}
by first localizing the fundamental class of 
$[\mathbb {P}(W_i)]$ and then pull–pushing the corresponding expression taking advantage of the fact that it is supported on a torus invariant subvariety.
For 
$0\leq j\leq i$, denote by 
$q_j$ the torus invariant point where only the 
$j$th homogeneous coordinate is non-zero. From Theorem 6.3 we have
\begin{equation} [\mathbb{P}(W_i)] = \sum_{j=0}^i \frac{[q_j]}{e(N_{q_j/\mathbb{P}(W_i)})}, \end{equation}
where the equivariant Euler class of the normal bundle to 
$q_j$ is the product of the 
$i$ tangent weights
\begin{equation} e(N_{q_j/\mathbb{P}(W_i)}) = \prod_{k\not=j}[((i-k) l_1+ kl_2)-((i-j) l_1+j l_2)] = (-1)^jj!(i-j)!(l_2-l_1)^i. \end{equation}
As both 
$p_1^\ast$ and 
$\pi _{1_{\ast }}$ are morphisms of 
$\mathcal {Q}$ modules, we have
\begin{equation} \pi_{1_{\ast}}(p_1^\ast([\mathbb{P}(W_i)])) = \sum_{j=0}^i (-1)^j\frac{\pi_{1_{\ast}}[q_j\times \mathbb{P}(W_{d-i}^{\oplus r+1})]}{j!(i-j)!(l_2-l_1)^i}. \end{equation} It remains to compute the equivariant Chow class of 
$\pi _{1_{\ast }}[q_j\times \mathbb {P}(W_{d-i}^{\oplus r+1})]$. One may see that 
$\pi _1$ maps the subspace 
$q_j\times \mathbb {P}(W_{d-i}^{\oplus r+1})$ isomorphically onto the linear subspace of 
$\mathbb {P}(W_{d}^{\oplus r+1})$ parameterizing 
$(r+1)$-tuples of polynomials which are divisible by 
$x^j$ and 
$y^{i-j}$. The class of this subspace corresponds to the product of the linear factors of the polynomial 
$P_{r,d}(H)$ corresponding to the homogeneous coordinates that vanish. By equivalently dividing 
$P_{r,d}(H)$ by the factors corresponding to the coordinates that do not vanish, one may write
\begin{equation} \pi_{1_{\ast}}[q_j\times \mathbb{P}(W_{d-i}^{\oplus r+1})] = \frac{P_{r,d}(H)}{\prod_{k=j}^{d-i+j} (H+(d-k)l_1+kl_2)^{r+1} }. \end{equation}
Plugging (48) into (47) and substituting 
$H= (({d+1})/{2}) c_1$ one readily obtains the expression in (43). We conclude the proof by observing that the ring 
$A^\ast _{\text { GL}_2}(\mathbb {P}(W_d)^{\oplus r+1})$ has no torsion, hence the integral coefficients Chow ring is included in the rational coefficients Chow ring. The classes computed via the Atyiah–Bott localization theorem are therefore correct.
Corollary 6.4 For any fixed values of 
$r,d>0$, the relations 
$\alpha _{i,0}$ for all values of 
$i$ are encoded in the generating function
\begin{equation} \mathcal{A}_{0}(d) = \sum_ {i =0}^d \alpha_{i,0} =\bigl[ \bigl( \text{e}^{t_1\partial_x+t_2\partial_y} \bigl(x^{{c_1}/{2(l_1-l_2)}+{d}/{2}} y^{{c_1}/{2(l_2-l_1)}+{d}/{2}} \bigr) \bigr)^{\odot r+1}_{|x=y=1} \bigr]_{| t_1 =t_2=1, \deg \leq dr }, \end{equation}
where the symbol 
$\odot$ refers to a Hadamard power for a two-variable exponential power series in variables 
$t_1/(l_1-l_2), t_2/(l_2-l_1)$, defined as follows:
\begin{equation}
\biggl(\sum_{\mu,\nu} a_{\mu,\nu}
\frac{\big({t_1}/({l_1-l_2})\big)^\mu}{\mu!}\frac{\big({t_2}/({l_2-l_1})\big)^\nu}{\nu!}\biggr)^{\odot
r+1} := \sum_{\mu,\nu} a_{\mu,\nu}^{r+1}
\frac{\big({t_1}/({l_1-l_2})\big)^\mu}{\mu!}\frac{\big({t_2}/({l_2-l_1})\big)^\nu}{\nu!}.
\end{equation}
Proof. We show that the degree 
$ri$ summand of (49) coincides with (43).
The exponential differential operator is in commuting variables and, hence, it admits the natural Taylor expansion:
\begin{equation} \text{e}^{t_1\partial_x+t_2\partial_y} = \sum_{\mu, \nu}\frac{t_1^\mu}{\mu!}\frac{t_2^\nu}{\nu!}\partial_x^\mu\partial_y^\nu. \end{equation}Applying the general summand in (51) to the monomial
\[ \bigl( x^{{c_1}/{2(l_1-l_2)}+{d}/{2}} y^{{c_1}/{2(l_2-l_1)}+{d}/{2}} \bigr) \]
and specializing 
$x=y=1$, one obtains
\begin{equation} \frac{t_1^\mu}{\mu!}\frac{t_2^\nu}{\nu!}\frac{(-1)^\mu}{(l_2-l_1)^{\mu+\nu}} \prod_{k=0}^{\mu-1} \biggl(\frac{c_1}{2}+\biggl(k-\frac{d}{2}\biggr)(l_2-l_1)\biggr)\prod_{m=0}^{\nu-1}\biggl(\frac{c_1}{2}+\biggl(\frac{d}{2}-m\biggr)(l_2-l_1)\biggr). \end{equation}
Reindexing the second product in (52) by 
$m = d-k$ one may rewrite (52) to obtain
\begin{equation} =\sum_{\mu,\nu}\frac{t_1^\mu}{\mu!}\frac{t_2^\nu}{\nu!}\frac{(-1)^\mu}{(l_2-l_1)^{\mu+\nu}} \frac{P_d}{ \prod_{k=\mu}^{d-\nu+1} \bigl({c_1}/{2}+(k-{d}/{2})(l_2-l_1)\bigr)}. \end{equation}
By the definition of Hadamard power in (50), taking the 
$(r+1)$th power of the power series in (53) has the effect of raising the last rational function to the power of 
$(r+1)$. The Chow degree of the coefficient of 
$t_1^\mu t_2^\nu$ is 
$(r+1)(\mu +\nu ) - (\mu +\nu ) = r(\mu +\nu )$, from which it follows that the degree 
$ri$ coefficient of the series is obtained by summing over all non-negative pairs of values of 
$\mu$ and 
$\nu$ adding to 
$i$. Setting 
$\mu = j, \nu = i-j$ one may immediately recognize formula (43).
Formula (43) allows us to also observe some structure of the relations 
$\alpha _{i,0}$ as the degree 
$d$ varies.
Corollary 6.5 For fixed values of 
$i$ and 
$r$, the coefficients of the classes 
$\alpha _{i,0}\in \mathbb {Z}[c_1,c_2]$ are polynomials in 
$d$ of degree 
$i(r+1)$.
7. Examples
7.1 Case $d=1$
Let us consider linear maps. The space 
$\mathcal {M}_{0}(\mathbb {P}^r,1)$ is the Grassmannian of lines in 
$\mathbb {P}^r$. The integral Chow ring of Grassmannians is well known (see, for example, [Reference Eisenbud and HarrisEH16, Theorem 5.26]), therefore, in this case, the result is not original but it allows us to show how to apply the formulas in the simplest case. Thanks to Theorem 4.3, the integral intersection ring of 
$\mathcal {M}_{0}(\mathbb {P}^r,1)$ has the form
\[ \mathbb{Z} [c_1,c_2]/I, \]
where 
$I$ is the ideal generated by the classes 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$. By replacing 
$d=1$ in (17) and (18), we get that the classes 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$ are the terms of total degree 
$r$ and 
$r+1$ in the power series expansion:
\[ \frac{1}{1 - c_1 + c_2} = 1 - (- c_1 + c_2) + (- c_1+c_2)^2 - \cdots. \]
The generating functions 
$\mathcal {A}_{1,0}(c_1,c_2,1)$ and 
$\mathcal {A}_{1,1}(c_1,c_2,1)$ from (17) and (18) are the same up to the constant term. This result is consistent with [Reference Eisenbud and HarrisEH16, Theorem 5.26] up to replacing our 
$c_1$ with 
$-c_1$.
7.2 Case $r=2$ and $d=3$
We explicitly determine the case of rational cubics in 
$\mathbb {P}^2$. By Theorem 4.3, the integral intersection ring of 
$\mathcal {M}_{0}(\mathbb {P}^2,3)$ has the form 
$\mathbb {Z} [c_1,c_2]/I,$ where 
$I$ is the ideal generated by the classes 
$\alpha _{1,0}$, 
$\alpha _{1,1}$, 
$\alpha _{2,0}$ and 
$\alpha _{3,0}$.
The generating functions for 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$, when 
$d=3$, are
\begin{align*} \mathcal{A}_{1,0}(3) &= \frac{3}{(1+c_1)(1-2c_1)+9c_2}=\frac{3}{1-c_1-2c_1^2 +9c_2}\\ &=3 \big( 1 + (c_1 + 2c_1^2 - 9c_2) + (c_1 + 2c_1^2 - 9c_2)^2 + \cdots \big);\\ \mathcal{A}_{1,1}(3) &= \frac{2c_1+2c_1^2 - 9c_2}{1-c_1-2c_1^2 +9c_2}=(2c_1+2c_1^2 - 9c_2) \big( 1 + (c_1 + 2c_1^2 - 9c_2) + (c_1 + 2c_1^2 - 9c_2)^2 + \cdots \big). \end{align*}
When 
$r=2$, the class 
$\alpha _{1,0}$ is the term of degree two of 
$\mathcal {A}_{1,0}(c_1,c_2,3)$. More precisely,
\[ \alpha_{1,0}=3(2c_1^2 - 9c_2 + c_1^2) = 9c_1^2 - 27 c_2. \]
On the other hand, the class 
$\alpha _{1,1}$ is the term of degree three of 
$\mathcal {A}_{1,1}(c_1,c_2,3)$, that is,
\[ \alpha_{1,1}=2c_1(3c_1^2 - 9c_2)+(2c_1^2 - 9c_2)(c_1) =8 c_1^3 - 27 c_1 c_2. \]
We apply formula (43) to determine 
$\alpha _{2,0}$ and 
$\alpha _{3,0}$. We use the following script on Maple that works for any values of 
$d$ and 
$r$:
Hence, we have
\begin{align*} \alpha_{2,0}&=12c_1^4 - 90c_1^2c_2 + 189c_2^2;\\ \alpha_{3,0}&= 4c_1^6 - 42c_1^4c_2 + 129c_1^2c_2^2 - 90c_2^3. \end{align*}
One can simplify the generators to write the final result in a more compact form as follows.
The class 
$\alpha _{2,0}$ is redundant because it belongs to the ideal generated by 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$. On the other hand, the class 
$\alpha _{3,0}$ does not belong to the ideal generated by 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$. One may easily check this as follows: taking a further quotient by the ideal generated by 
$c_1$ and 
$27$, we get 
$\alpha _{1,0}\equiv \alpha _{1,1}\equiv 0$ but 
$\alpha _{3,0}\equiv 9c_2^3 \not \equiv 0$. One can also see that
\[ 3(6c_2^2c_1^2+9c_2^3) = -c_2^2(9c_1^2 -27c_2) +c_1c_2(27c_1c_2), \]
showing, in particular, that the class 
$3\alpha _{3,0}$ is in the ideal generated by 
$\alpha _{1,0}$ and 
$\alpha _{1,1}$. In conclusion, we have shown the following result.
Theorem 7.1 We have the isomorphism:
\[ A^* \big( \mathcal{M}_{0}\big( \mathbb{P}^2, 3 \big) \big) \cong \frac{\mathbb{Z}[c_1,c_2]}{(9c_1^2 - 27c_2,\; c_1^3,\; 6c_2^2c_1^2+9c_2^3)}. \]
As seen in Theorem 7.1, the set of generators described in Theorem 4.3 is not necessarily minimal. We propose the following conjecture.
Conjecture 7.2 Let 
$r$ be a positive integer and 
$d$ a positive odd number. Then
\[ A^* \big( \mathcal{M}_{0}\big( \mathbb{P}^r, d \big) \big) \cong \frac{\mathbb{Z}[c_1,c_2]}{(\alpha_{1,0}, \alpha_{1,1}, \{ \alpha_{p,0} \mid p\text{ is a prime that divides }d \}) }. \]
Further, all the relations listed are necessary.
Seth Ireland programmed a 
${\tt Macaulay2}$ code that provided extensive verification for this conjecture [Reference IrelandIre22]. At this point we know the conjecture to be true for 
$r \leq 9$, 
$d\leq 49$. A weaker version of the conjecture, asserting generation but not minimality, has been verified for 
$r\leq 5$, 
$d\leq 99$.
Acknowledgements
We would like to thank S. Ireland for writing the code that gave extensive verifications of Conjecture 7.2 and C. Peterson for several conversations related to the project. We are grateful to R. Pandharipande, J. Bryan, T. Graber and the participants of the UBC-ETH intercontinental algebraic geometry and moduli zoominar as well as R. Vakil, J. Kass, P. Petrov and the participants of the Stanford virtual algebraic geometry seminar for the many interesting questions and observations following the presentation of this work. We gratefully acknowledge the following funding institutions: R.C. is supported by NSF grant DMS-2100962 and D.F. is supported by Simons collaboration grant 360311. The authors would also like to thank the reviewers for their helpful comments and suggestions.
Open access
