We apply the endoscopic classification of automorphic forms on $U(3)$ to study the growth of the first Betti number of congruence covers of a Picard modular surface. As a consequence, we establish a case of a conjecture of Sarnak and Xue on cohomology growth.

We endow certain GKZ-hypergeometric systems with a natural structure of a mixed Hodge module, which is compatible with the mixed Hodge module structure on the Gauß–Manin system of an associated family of Laurent polynomials. As an application we show that the underlying perverse sheaf of a GKZ-system with rational parameter has quasi-unipotent local monodromy.

We introduce a new class of autoequivalences that act on the derived categories of certain vector bundles over Grassmannians. These autoequivalences arise from Grassmannian flops: they generalize Seidel–Thomas spherical twists, which can be seen as arising from standard flops. We first give a simple algebraic construction, which is well suited to explicit computations. We then give a geometric construction using spherical functors which we prove is equivalent.

Let 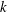$k$ be a field and 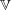$\mathbb{V}$ the affine threefold in 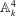$\mathbb{A}^4_k$ defined by 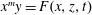$x^m y=F(x, z, t)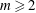$, $m \ge 2$. In this paper, we show that 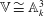$\mathbb{V} \cong \mathbb{A}^3_k$ if and only if 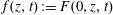$f(z, t): = F(0, z, t)$ is a coordinate of 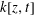$k[z, t]$. In particular, when 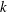$k$ is a field of positive characteristic and 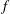$f$ defines a non-trivial line in the affine plane 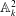$\mathbb{A}^2_k$ (we shall call such a 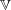$\mathbb{V}$ as an Asanuma threefold), then 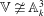$\mathbb{V}\ncong \mathbb{A}^3_k$ although 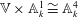$\mathbb{V} \times \mathbb{A}^1_k \cong \mathbb{A}^4_k$, thereby providing a family of counter-examples to Zariski’s cancellation conjecture for the affine 3-space in positive characteristic. Our main result also proves a special case of the embedding conjecture of Abhyankar–Sathaye in arbitrary characteristic.

We generalize the injectivity theorem of Esnault and Viehweg, and apply it to the structure of log canonical type divisors.

Finite $W$-algebras are certain associative algebras arising in Lie theory. Each $W$-algebra is constructed from a pair of a semisimple Lie algebra ${\mathfrak{g}}$ (our base field is algebraically closed and of characteristic 0) and its nilpotent element $e$. In this paper we classify finite-dimensional irreducible modules with integral central character over $W$-algebras. In more detail, in a previous paper the first author proved that the component group $A(e)$ of the centralizer of the nilpotent element under consideration acts on the set of finite-dimensional irreducible modules over the $W$-algebra and the quotient set is naturally identified with the set of primitive ideals in $U({\mathfrak{g}})$ whose associated variety is the closure of the adjoint orbit of $e$. In this paper, for a given primitive ideal with integral central character, we compute the corresponding $A(e)$-orbit. The answer is that the stabilizer of that orbit is basically a subgroup of $A(e)$ introduced by G. Lusztig. In the proof we use a variety of different ingredients: the structure theory of primitive ideals and Harish-Chandra bimodules for semisimple Lie algebras, the representation theory of $W$-algebras, the structure theory of cells and Springer representations, and multi-fusion monoidal categories.