Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T16:53:23.178Z Has data issue: false hasContentIssue false
  • English
  • Français

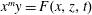On the family of affine threefolds $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x^m y= F(x, z, t)$

Part of: Affine geometry Ring extensions and related topics General commutative ring theory

Published online by Cambridge University Press:  09 June 2014

Neena Gupta
Neena Gupta*
Affiliation:
Stat-Math Unit, Indian Statistical Institute, 203 B.T. Road, Kolkata 700108, India email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

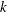Let $k$ be a field and 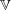$\mathbb{V}$ the affine threefold in 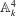$\mathbb{A}^4_k$ defined by 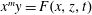$x^m y=F(x, z, t)$, 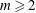$m \ge 2$. In this paper, we show that 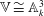$\mathbb{V} \cong \mathbb{A}^3_k$ if and only if 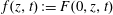$f(z, t): = F(0, z, t)$ is a coordinate of 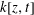$k[z, t]$. In particular, when 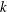$k$ is a field of positive characteristic and 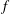$f$ defines a non-trivial line in the affine plane 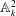$\mathbb{A}^2_k$ (we shall call such a 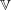$\mathbb{V}$ as an Asanuma threefold), then 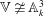$\mathbb{V}\ncong \mathbb{A}^3_k$ although 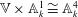$\mathbb{V} \times \mathbb{A}^1_k \cong \mathbb{A}^4_k$, thereby providing a family of counter-examples to Zariski’s cancellation conjecture for the affine 3-space in positive characteristic. Our main result also proves a special case of the embedding conjecture of Abhyankar–Sathaye in arbitrary characteristic.

Keywords

polynomial algebragraded ringGa-actionDerksen invariantMakar-Limanov invariantcancellation problemembedding problemA2-fibrationlocalization theorem of K-theory

MSC classification

Secondary: 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem) 14R25: Affine fibrations 13B25: Polynomials over commutative rings 13A50: Actions of groups on commutative rings; invariant theory
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 6 , June 2014 , pp. 979 - 998
Copyright
© The Author 2014 

References

Abhyankar, S., Lectures on expansion techniques in algebraic geometry (Notes by Balwant Singh), Tata Institute of Fundamental Research Lectures on Mathematics and Physics, vol. 57 (Tata Institute of Fundamental Research, Bombay, 1977).Google Scholar
Abhyankar, S., Eakin, P. and Heinzer, W., On the uniqueness of the coefficient ring in a polynomial ring, J. Algebra 23 (1972), 310–342.Google Scholar
Asanuma, T., Polynomial fibre rings of algebras over Noetherian rings, Invent. Math. 87 (1987), 101–127.CrossRefGoogle Scholar
Asanuma, T., Non-linearizable algebraic group actions on An, J. Algebra 166 (1994), 72–79.CrossRefGoogle Scholar
Bhatwadekar, S. M. and Dutta, A. K., Linear planes over a discrete valuation ring, J. Algebra 166 (1994), 393–405.Google Scholar
Crachiola, A. J., The hypersurface x + x 2y + z 2 + t 3 = 0 over a field of arbitrary characteristic, Proc. Amer. Math. Soc. 134 (2005), 1289–1298.Google Scholar
Derksen, H., Hadas, O. and Makar-Limanov, L., Newton polytopes of invariants of additive group actions, J. Pure Appl. Algebra 156 (2001), 187–197.Google Scholar
Freudenburg, G. and Russell, P., Open problems in affine algebraic geometry, in Affine algebraic geometry, Contemporary Mathematics, vol. 369 (American Mathematical Society, Providence, RI, 2005), 1–30.Google Scholar
Fujita, T., On Zariski problem, Proc. Japan Acad. 55 (1979), 106–110.Google Scholar
Ganong, R., The pencil of translates of a line in the plane, in Affine algebraic geometry, CRM Proceedings Lecture Notes, vol. 54 (American Mathematical Society, Providence, RI, 2011), 57–71.Google Scholar
Gupta, N., On the cancellation problem for the affine space A3 in characteristic p, Invent. Math. 195 (2014), 279–288, doi:10.1007/s00222-013-0455-2.Google Scholar
Kaliman, S., Polynomials with general ℂ2-fibers are variables, Pacific J. Math. 203 (2002), 161–190.Google Scholar
Kaliman, S., Vénéreau, S. and Zaidenberg, M., Simple birational extensions of the polynomial algebra ℂ[3], Trans. Amer. Math. Soc. 356 (2004), 509–555.CrossRefGoogle Scholar
Makar-Limanov, L., On the hypersurface x + x 2y + z 2 + t 3 = 0 in ℂ4 or a ℂ3-like threefold which is not ℂ3, Israel J. Math. B 96 (1996), 419–429.Google Scholar
Makar-Limanov, L., On the group of automorphism of a surface x ny = P (z), Israel J. Math. 121 (2001), 113–123.Google Scholar
Miyanishi, M. and Sugie, T., Affine surfaces containing cylinderlike open sets, J. Math. Kyoto Univ. 20 (1980), 11–42.Google Scholar
Nagata, M., On automorphism group of k[x, y], Lectures in Mathematics, vol. 5 (Kyoto University, Tokyo, 1972).Google Scholar
Russell, P., Simple birational extensions of two dimensional affine rational domains, Compositio Math. 33 (1976), 197–208.Google Scholar
Russell, P., On affine-ruled rational surfaces, Math. Ann. 255 (1981), 287–302.Google Scholar
Russell, P. and Sathaye, A., On finding and cancelling variables in k[X, Y, Z], J. Algebra 57 (1979), 151–166.Google Scholar
Sathaye, A., On linear planes, Proc. Amer. Math. Soc. 56 (1976), 1–7.CrossRefGoogle Scholar
Sathaye, A., Polynomial ring in two variables over a D.V.R.: A criterion, Invent. Math. 74 (1983), 159–168.Google Scholar
Segre, B., Corrispondenze di Möbius e trasformazioni cremoniane intere, Atti Accad. Sci. Torino. Cl. Sci. Fis. Mat. Natur. 91 (1956/1957), 3–19 (in Italian).Google Scholar
Srinivas, V., Algebraic K-theory (Birkhäuser, Boston, 2008).Google Scholar
Veǐsfeǐler, B. and Dolgačev, I.  V., Unipotent group schemes over integral rings, Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 757–799 (in Russian).Google Scholar