A collection of permutation classes is exhibited whose growth rates form a perfect set, thereby refuting some conjectures of Balogh, Bollobás and Morris.

Let q be a power of a prime p, and let n, d, ℓ be integers such that 1 ≤ n, 1 ≤ ℓ < q. Consider the modulo q complete ℓ-wide family:

We describe a Gröbner basis of the vanishing ideal I() of the set of characteristic vectors of over fields of characteristic p. It turns out that this set of polynomials is a Gröbner basis for all term orderings ≺, for which the order of the variables is xn ≺ xn−1 ≺ ⋅⋅⋅ ≺ x1.

We compute the Hilbert function of I(), which yields formulae for the modulo p rank of certain inclusion matrices related to .

We apply our results to problems from extremal set theory. We prove a sharp upper bound of the cardinality of a modulo q ℓ-wide family, which shatters only small sets. This is closely related to a conjecture of Frankl [13] on certain ℓ-antichains. The formula of the Hilbert function also allows us to obtain an upper bound on the size of a set system with certain restricted intersections, generalizing a bound proposed by Babai and Frankl [6].

The paper generalizes and extends the results of [15], [16] and [17].

Using various results from extremal set theory (interpreted in the language of additive combinatorics), we prove an asymptotically sharp version of Freiman's theorem in : if is a set for which |A + A| ≤ K|A| then A is contained in a subspace of size ; except for the error, this is best possible. If in addition we assume that A is a downset, then we can also cover A by O(K46) translates of a coordinate subspace of size at most |A|, thereby verifying the so-called polynomial Freiman–Ruzsa conjecture in this case. A common theme in the arguments is the use of compression techniques. These have long been familiar in extremal set theory, but have been used only rarely in the additive combinatorics literature.

A celebrated theorem of Friedgut says that every function f : {0, 1}n → {0, 1} can be approximated by a function g : {0, 1}n → {0, 1} with 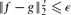, which depends only on eO(If / ε) variables, where If is the sum of the influences of the variables of f. Dinur and Friedgut later showed that this statement also holds if we replace the discrete domain {0, 1}n with the continuous domain [0, 1]n, under the extra assumption that f is increasing. They conjectured that the condition of monotonicity is unnecessary and can be removed.

We show that certain constant-depth decision trees provide counter-examples to the Dinur–Friedgut conjecture. This suggests a reformulation of the conjecture in which the function g : [0, 1]n → {0, 1}, instead of depending on a small number of variables, has a decision tree of small depth. In fact we prove this reformulation by showing that the depth of the decision tree of g can be bounded by eO(If / ε2).

Furthermore, we consider a second notion of the influence of a variable, and study the functions that have bounded total influence in this sense. We use a theorem of Bourgain to show that these functions have certain properties. We also study the relation between the two different notions of influence.

An instance of a size-n stable marriage problem involves n men and n women, each individually ranking all members of opposite sex in order of preference as a potential marriage partner. A complete matching, a set of n marriages, is called stable if no unmatched man and woman prefer each other to their partners in the matching. It is known that, for every instance of marriage partner preferences, there exists at least one stable matching, and that there are instances with exponentially many stable matchings. Our focus is on a random instance chosen uniformly from among all (n!)2n possible instances. The second author had proved that the expected number of stable marriages is of order nlnn, while its likely value is of order n1/2−o(1) at least. In this paper the second moment of that number is shown to be of order (nlnn)2. The combination of the two moment estimates implies that the fraction of problem instances with roughly cnlnn solutions is at least 0.84. Whether this fraction is asymptotic to 1 remains an open question.

An exact formula for the expected length of the minimum spanning tree of a connected graph, with independent and identical edge distribution, is given, which generalizes Steele's formula in the uniform case. For a complete graph, the difference of expected lengths between exponential distribution, with rate one, and uniform distribution on the interval (0, 1) is shown to be positive and of rate ζ(3)/n. For wheel graphs, precise values of expected lengths are given via calculations of the associated Tutte polynomials.

Let k3reg(n, d) be the minimum number of triangles in d-regular graphs with n vertices. We find the exact value of k3reg(n, d) for d between and n/2. In addition, we identify the structure of the extremal graphs.

A d-simplex is a collection of d + 1 sets such that every d of them has non-empty intersection and the intersection of all of them is empty. Fix k ≥ d + 2 ≥ 3 and let be a family of k-element subsets of an n-element set that contains no d-simplex. We prove that if , then there is a vertex x of such that the number of sets in omitting x is o(nk−1) (here o(1)→ 0 and n → ∞). A similar result when n/k is bounded from above was recently proved in [10].

Our main result is actually stronger, and implies that if for any ϵ < 0 and n sufficiently large, then contains d + 2 sets A, A1, . . . ,Ad+1 such that the Ais form a d-simplex, and A contains an element of ∩j≠iAj for each i. This generalizes, in asymptotic form, a recent result of Vestraëte and the first author [18], who proved it for d = 1, ϵ = 0 and n ≥ 2k.

Let r ≥ 3 and (c/rr)r log n ≥ 1. If G is a graph of order n and its largest eigenvalue μ(G) satisfies then G contains a complete r-partite subgraph with r − 1 parts of size ⌊(c/rr)r log n⌋ and one part of size greater than n1−cr−1.

This result implies the Erdős–Stone–Bollobás theorem, the essential quantitative form of the Erdős–Stone theorem. Another easy consequence is that if F1, F2, . . . are r-chromatic graphs satisfying v(Fn) = o(log n), then