Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T13:25:24.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic Properties of Modulo q Complete ℓ-Wide Families

Published online by Cambridge University Press:  01 May 2009

BÁLINT FELSZEGHY ,
GÁBOR HEGEDŰS  and
LAJOS RÓNYAI
BÁLINT FELSZEGHY
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, Budapest, Hungary (e-mail: [email protected])
GÁBOR HEGEDŰS
Affiliation:
Kecskemét, Hungary (e-mail: [email protected])
LAJOS RÓNYAI
Affiliation:
Computer and Automation Institute, Hungarian Academy of Sciences, Budapest, Hungary and Institute of Mathematics, Budapest University of Technology and Economics, Budapest, Hungary (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let q be a power of a prime p, and let n, d, ℓ be integers such that 1 ≤ n, 1 ≤ ℓ < q. Consider the modulo q complete ℓ-wide family:

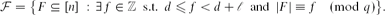
We describe a Gröbner basis of the vanishing ideal I(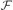) of the set of characteristic vectors of 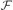over fields of characteristic p. It turns out that this set of polynomials is a Gröbner basis for all term orderings ≺, for which the order of the variables is xn ≺ xn−1 ≺ ⋅⋅⋅ ≺ x1.

We compute the Hilbert function of I(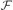), which yields formulae for the modulo p rank of certain inclusion matrices related to .

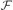We apply our results to problems from extremal set theory. We prove a sharp upper bound of the cardinality of a modulo q ℓ-wide family, which shatters only small sets. This is closely related to a conjecture of Frankl [13] on certain ℓ-antichains. The formula of the Hilbert function also allows us to obtain an upper bound on the size of a set system with certain restricted intersections, generalizing a bound proposed by Babai and Frankl [6].

The paper generalizes and extends the results of [15], [16] and [17].

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 3 , May 2009 , pp. 309 - 333
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Adams, W. W. and Loustaunau, P. (1994) An Introduction to Gröbner Bases, AMS.CrossRefGoogle Scholar
[2]Alon, N. (1999) Combinatorial Nullstellensatz. Combin. Probab. Comput. 8 7–29.CrossRefGoogle Scholar
[3]Alon, N. (2000) Algebraic and probabilistic methods in discrete mathematics. Geom. Funct. Anal. Special Volume, Part II 455–470.CrossRefGoogle Scholar
[4]Alon, N., Babai, L. and Suzuki, H. (1991) Multilinear polynomials and Frankl–Ray-Chaudhuri–Wilson type intersection theorems. J. Combin. Theory Ser. A 58 165–180.CrossRefGoogle Scholar
[5]Anstee, R. P., Rónyai, L. and Sali, A. (2002) Shattering news. Graphs Combin. 18 59–73.CrossRefGoogle Scholar
[6]Babai, L. and Frankl, P. (1992) Linear Algebra Methods in Combinatorics, Preliminary Version 2, September 1992.Google Scholar
[7]Babai, L., Frankl, P., Kutin, S. and Štefankovič, D. (2001) Set systems with restricted intersections modulo prime powers. J. Combin. Theory Ser. A 95 39–73.CrossRefGoogle Scholar
[8]Bernasconi, A. and Egidi, L. (1999) Hilbert function and complexity lower bounds for symmetric Boolean functions. Inform. Comput. 153 1–25.CrossRefGoogle Scholar
[9]Buchberger, B. and Winkler, F., eds (2001) Gröbner Bases and Applications, Cambridge University Press.Google Scholar
[10]Deza, M., Frankl, P. and Singhi, N. M. (1981) On functions of strength t. Combinatorica 3 331–339.CrossRefGoogle Scholar
[11]Einstein, O. and Hassin, R. (2005) The number of solutions sufficient for solving a family of problems. Math. Oper. Res. 30 880–896.CrossRefGoogle Scholar
[12]Felszeghy, B., Ráth, B. and Rónyai, L. (2006) The lex game and some applications. J. Symbol. Comput. 41 663–681.CrossRefGoogle Scholar
[13]Frankl, P. (1989) Traces of antichains. Graphs Combin. 5 295–299.CrossRefGoogle Scholar
[14]Frankl, P. and Wilson, R. M. (1981) Intersection theorems with geometric consequences. Combinatorica 1 357–368.CrossRefGoogle Scholar
[15]Friedl, K., Hegedűs, G. and Rónyai, L. (2007) Gröbner bases for complete ℓ-wide families. Publicationes Math. Debrecen 70 271–290.CrossRefGoogle Scholar
[16]Hegedűs, G. and Rónyai, L. (2003) Gröbner bases for complete uniform families. J. Algebraic Combin. 17 171–180.CrossRefGoogle Scholar
[17]Hegedűs, G. and Rónyai, L. (2003) Standard monomials for q-uniform families and a conjecture of Babai and Frankl. Central Europ. J. Math. 1 198–207. http://www.cesj.com/mathematics.htmlCrossRefGoogle Scholar
[18]Hillar, C. J. and Windfeldt, T. (2008) Algebraic characterization of uniquely vertex colorable graphs. J. Combin. Theory Ser. B 98 400–414.CrossRefGoogle Scholar
[19]Qian, J. and Ray-Chaudhuri, D. K. (2000) On mod-p Alon–Babai–Suzuki inequality. J. Algebraic Combin. 12 85–93.CrossRefGoogle Scholar
[20]Sauer, N. (1972) On the density of families of sets. J. Combin. Theory Ser. A 13 145–147.CrossRefGoogle Scholar
[21]Shelah, S. (1972) A combinatorial problem: Stability and order for models and theories in infinitary languages. Pacific J. Math. 41 247–261.CrossRefGoogle Scholar
[22]Tao, T. and Vu, V. (2006) Additive Combinatorics, Vol. 105 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
[23]Vapnik, V. N. and Chervonenkis, A. Y. (1971) On the uniform convergence of relative frequencies of events to their probabilities. Theory Probab. Appl. XVI 264–280.CrossRefGoogle Scholar
[24]Wilson, R. M. (1990) A diagonal form for the incidence matrices of t-subsets vs. k-subsets. Europ. J. Combin. 11 609–615.CrossRefGoogle Scholar